Neural Graph Collaborative Filtering (SIGIR 2019)
13 Jan 2022
Matrix Factorization, Neural Collaborative Filtering 혹은 CF 관련된 기본적인 내용은 생략했습니다. 다 읽고 보니, NCF에서 사용한 데이터셋인 Movie Lens를 사용하진 않지만 implicit feedback 데이터를 쓰고, negative sampling을 통해 interaction이 없는 데이터셋을 만드는것이 동일하여 MovieLens dataset 또한 사용해볼 수 있을것같다.
내가 생각한 Neural Graph Collaborative Filtering에서의 핵심은 다음과 같다.
-
이전의 MF, NeuMF 등과 같은 다른 work들은 CF signal을 implicit하게 encode했다. NGCF에서는 embedding propagation layer를 쌓음으로써, high-order connectivity에서 collaborative signal을 capture할 수 있다. 이 방법은 explicit하게 user와 item간의 interaction을 encode하는 방법으로, desired한 recommendation을 가능하게 해준다.
-
user-item interaction에 대한 graph는 laplacian matrix를 이용하여 구현한다. laplacian matrix는 adjacent matrix와 degree matrix를 이용하여 각 노드(user 혹은 item)을 나타낸다. normalized laplacian matrix를 각 user, item에 곱하는 것 대신 Propagation Rule in Matrix Form 을 사용하여 한번에 계산한다.
- NGCF은 크게 3가지의 layer로 이뤄진다.
- user,item embedding layer.
- high-order connectivity relation을 고려하여 embedding을 refine(=update)하는 multiple embedding propagation layer. (논문에서는 3개의 embedding propagation layer를 사용했다.)
- different propagation layer들로부터 refine된 embedding을 모두 합쳐서 user-item pair의 affinity score(관련성 점수)를 출력하는 prediction layer. (이때 prediction은 단순히 concatenation된 user와 item의 inner product이다.)
- NGCF에서는 Dataset에 interaction의 유무만을 나타내는 implicit feedback dataset을 사용했다. Negative sampling을 통해 dataset에 negative instance를 생성하여 NDCG, HitRatio 지표를 평가하였다. (NeuMF(NCF)에서 사용했던 MovieLens를 그대로 사용해도 괜찮을것 같다.)
다음 repository에 NGCF를 구현했습니다.
Abstract
user와 item 대한 vector representation을 학습하는 것은 현대의 modern recommender system에서 핵심적인 일이다. 이전의 MF와 같은 방식들은 user와 item에 대해서 embedding process를 통해 latent factor를 학습하게 된다. 하지만 embedding들이 collaborative filtering effect을 capture하는데 충분하지 않다. 이 논문에서는 embedding을 propagate 시키는 user-item graph structure를 사용하는 Neural Graph Collaborative Filtering을 개발하고자 한다. 이 모델은 user-item graph에서의 high-order connectivity를 잘 나타낸다.
1. Introduction
MF, NCF 등은 효율적이지만, 여기에 사용되는 embedding들은 CF의 user,item을 표현하는 데 있어서 충분하지 않다. user와 item에 관한 behavior similarity를 표현하는 latent factor인 collaborative signal을 encode하는 것에 대해 부족하다. user-item interaction을 고려하지 않는 feature들을 사용하는 대부분 method에서의 embedding function들은 model training에서 objective function을 정의하는 데에만 사용한다.
user-item interaction을 embedding function에 합치면 더 유용할 질것이다. 하지만, scale of interaction이 millions를 넘어 매우 커질 수 있고, 이로인해 desired collaborative signal을 구분하지 못할 수 도 있다. 이 논문에서는 이 interaction graph 구조에서의 collaborative signal을 해석하여 user-item interaction의 high-order connectivity를 이용하는 방법으로 위에서 말한 challenge를 해결한다.
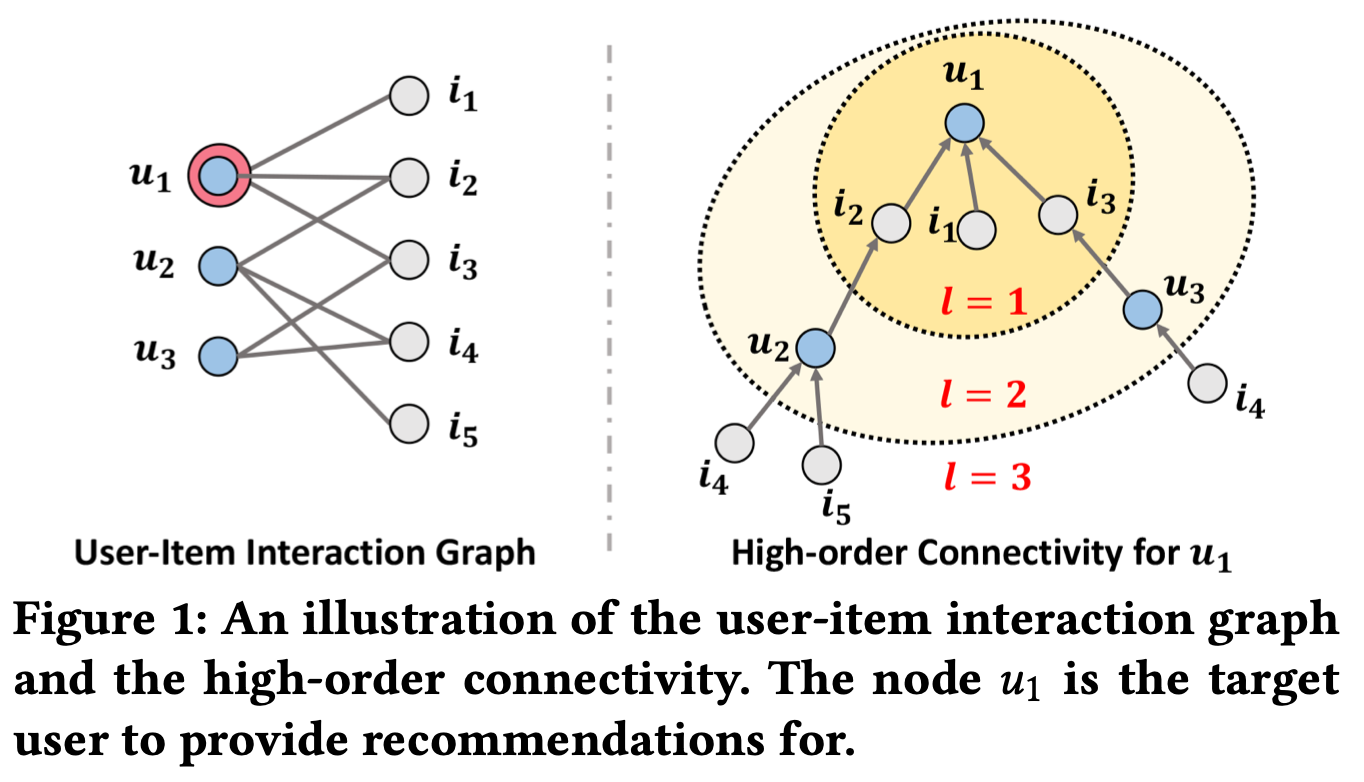
Figure 1이 high-order connectivity concept을 설명해준다. 왼쪽 그림에서 user $u_1$이 관심있는 item들과 연결되어있고, 오른쪽 그림이 user-item interaction을 표현하고 있다. 오른쪽 그림에서 u1으로부터 expand되는 트리 구조를 보여준다. high-order connectivity는 길이 1 이상의 어떠한 path에서 $u_1$에 도달 하는 path를 의미한다. 이러한 high-order connectivity는 collaborative signal에 관한 rich semantic을 포함한다.
오른쪽 그림에서 $u_1\leftarrow i_2 \leftarrow u_2$의 경로를 보면, $u_1, u_2$ 둘다 $i_2$를 interact한 behavior similarity를 나타낸다. 또한 $u_1\leftarrow i_2 \leftarrow u_2 \leftarrow i_4$를 보면, $u_1$와 유사한 $u_2$가 이전에 $i_4$를 소비한 것을 볼 수 있다.
본 논문에서는 embedding function에 high-order connectivity를 모델링 하고자 한다. tree와 같은 interaction graph를 확장하는 것 대신, graph에서 재귀적으로 embedding을 propagate 시키기 위한 neural network을 구축했다. 이 방법은 embedding space에서 information flow를 구축하는 GNN의 영감을 받았다. 특히, interacted item들의 embedding을 합침으로써 user의 embedding을 update할 수 있는 embedding propagation layer를 고안했다. 여러개의 embedding propagation layer를 쌓음으로써, high-order connectivities에서 collaborative signal을 capture할 수 있다.
$u_1\leftarrow i_2 \leftarrow u_2$ : 2개의 layer를 쌓은것.
$u_1\leftarrow i_2 \leftarrow u_2 \leftarrow i_4$ : 3개의 layer를 쌓은것.
information flow의 힘에 따라 추천 우선순위를 결정할 수 있다. 여러 benchmark dataset에 NGCF 방법의 효율성과 합리성을 입증하기 위해 사용했다.
2. Methodlogy
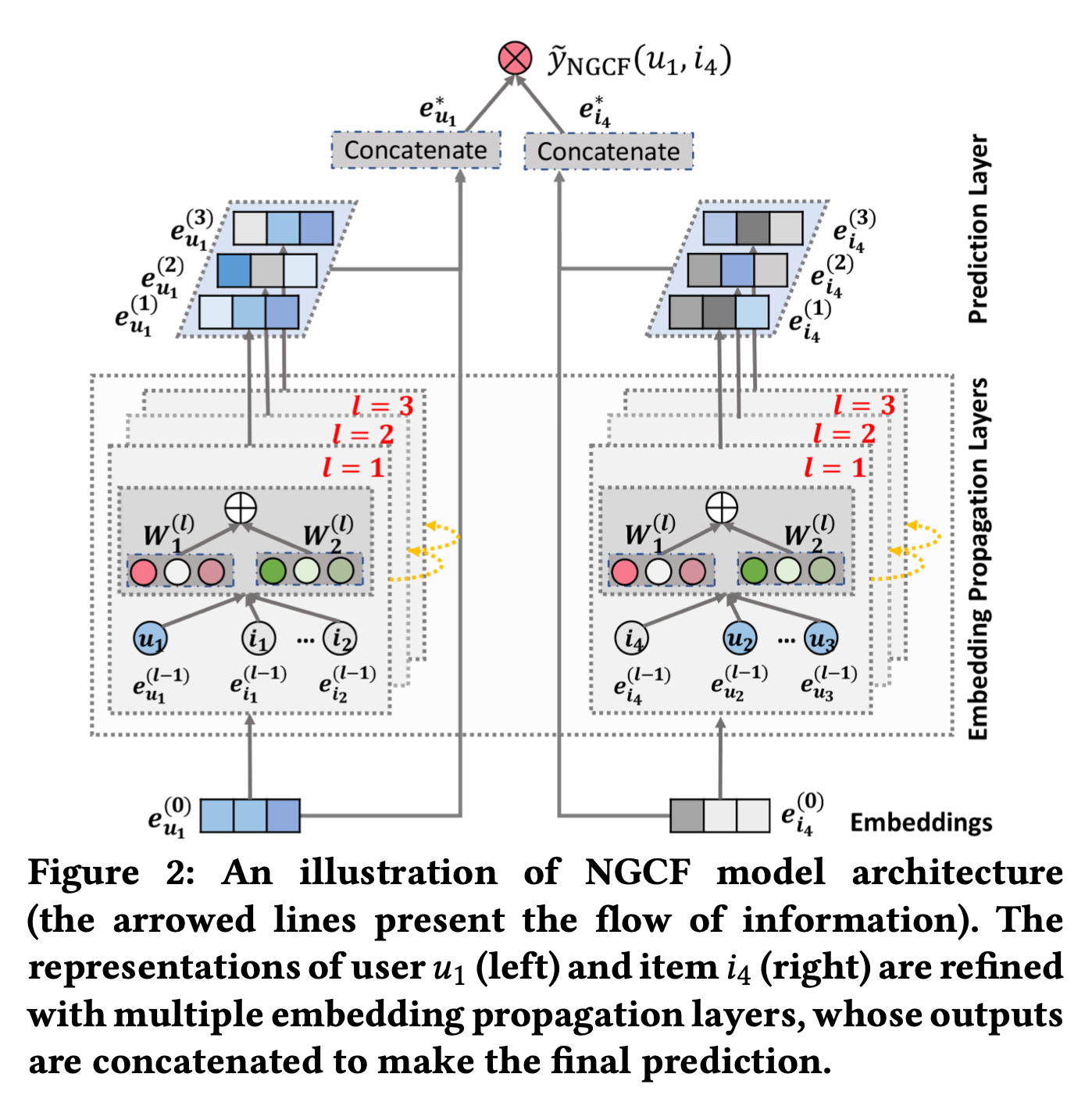
Figure 2가 전반적인 NGCF 구조를 나타내고 있다. NGCF framework에는 3개의 component가 있다.
- user,item embedding을 initialization하는 embedding layer.
- high-order connectivity relation들을 사용하여 embedding을 refine하는 multiple embedding propagation layer.
- different propagation layer들로부터 refine된 embedding을 모두 합쳐서 user-item pair의 affinity score(관련성 점수)를 출력하는 prediction layer.
위 세가지 component를 설명하고 나서, NGCF의 복잡성에 대해 설명한다.
2.1 Embedding Layer
user u에 대한 embedding vector를 $e_u\in R^d$, item i에 대한 embedding vector를 $e_i \in R^d$ 로 나타내고, d는 embedding size를 의미한다. embedding은 look-up table로써, parameter matrix를 build하는 것을로 볼수 있다.
$E = [e_{u_1},…,e_{u_N}, e_{i_1},…,e_{i_M}]$
이것은 user embedding과 item embedding들에 대한 initial state를 표현하는 embedding table의 역할을 하고, end-to-end 방식으로 optimize된다. 전통적인 추천시스템 모델인 MF, NCF와 같은 방법은 이러한 ID embedding을 interaction layer에 집어넣어 prediction score를 계산한다. 하지만 NGCF에서는 user-item interaction에서 embedding들을 propagation하는 것을 통해 embedding을 update 한다. 추천 시스템을 위한 더 효과적인 embedding을 구현할 수 있고, 이러한 embedding refinement step이 collaborative signal를 embedding에 넣을 수 있다.
2.2 Embedding Propagation Layers
그 다음 graph structure에서의 CF signal을 capture하기 위해 GNN message-passing 구조를 build했고, users와 items의 embedding을 refine했다. 일단 one-layer propagation design을 설명하고, 여러 연속적인 layer들에 대해서 generalize할 것이다.
2.2.1 First-order propagation
interacted items들은 user의 선호에 대한 direct evidence를 제공한다. item을 소비한 user들은 item들의 feature로 다뤄질 수 있고, 2개의 item의 collaborative similarity를 측정하는데 사용할 수 있다. 연결된 user들과 item들 사이의 embedding propagation을 구현하기 위해, 두가지 main operation인 message construction과 message aggregation을 이용해 process를 공식화 하였다.
Message Construction : 연결된 user-item pair (u,i)에 대해, item i 에서 user u로 가는 message를 다음과 같이 정의했다.
$m_{u\leftarrow i}=f(e_i,e_u,p_{ui})$
- $m_{u\leftarrow i}$ : message embedding, propagate되는 information을 의미한다.
- $f()$ : input으로 $e_u,e_i$를 사용하고, $p_{ui}$를 coefficient를 사용하는 message encoding function을 의미한다.
$f()$를 다음과 같이 구현했다.
$m_{u\leftarrow i}={1\over{\sqrt \mid N_u \mid \mid N_i \mid}} (W_1e_i+W_2(e_i\odot e_u))$
- $W_1,W_2\in R^{d’Xd}$: trainable weight matrices로, propagation을 위한 userful한 information을 distill시켜 준다. $d’$은 transformation size이다.
- $e_i$의 contribution만 고려하는 기존의 graph convolution network와 달리, $e_i\odot e_u$를 통해 전달되는 message에서 $e_u,e_i$ 둘 사이의 관계의 interaction을 고려한다. 이것은 message가 $e_u,e_i$의 관계에 더 dependent하게 만들어서, 비슷한 아이템들로 부터 더 많은 message를 전달한다. 이것이 model representation 능력을 향상시키고, 추천시스템 성능을 높여준다. (4.4.2에서 입증되었다.)
- $p_{ui}={1\over{\sqrt \mid N_u \mid \mid N_i \mid}}$ : graph Laplacian norm이고, $N_u,N_i$ 는 user u와 item i의 first-hop neighbor를 나타낸다. representation learning관점에서, 이것은 historical item이 얼마나 user preference에 영향을 주는지 의미한다. message passing 관점에서는, $p_{ui}$는 discount factor로 해석될 수 있으며, 전파되는 메시지는 path length에 따라 감소하게된다.
Message Aggregation: 이 단계에서는 user u의 representation을 refine하기 위해 u의 neighborhood로부터의 전달된 메시지를 합친다.
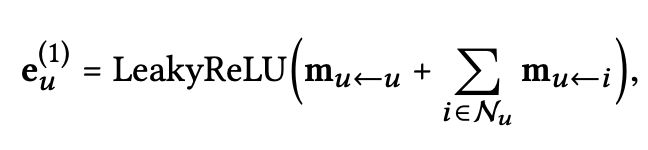
- $e^{(1)}_u$: first embedding propagation layer이후에 얻어진 user u의 representation을 의미한다.
- LeakyReLU는 positive, small negative signal 모두를 encode하게 해준다.
- neighbor $N_u$로부터 전파된 메시지들에 대해서, $m_{u\leftarrow u}=W_1e_u$와 같이 u의 self-connection을 고려한다. 그리고 이것은 orginal feature로부터 정보를 얻을 수 있게 한다.
Message Construction에서 $m_{u\leftarrow i}$만 다루고, $m_{u\leftarrow u}$는 다루지 않았는데, i대신 u를 대입하면 된다.
- 같은 방식으로 item에도 적용할 수 있다.
- 요약하면, embedding propagation layer의 이점은 user와 item의 representation을 연관시키기 위해 first-order connectivity information을 explicit하게 이용한 것이다.
2.2.2 High-order Propagation
first-order connectivity modeling에 의해 augment된 representation으로, high-order connectivity information을 얻기 위해 더 많은 embedding propagation layer를 쌓을 수 있다. 이러한 high-order connectivities는 user와 item사이의 relevance score를 estimate하기 위한 collaborative signal을 encode할때 중요하다.
l개의 embedding propagation layer를 쌓음으로써, user는 l-hop neighbor로부터 전파된 메시지를 받을 수 있다. Figure 2에서 볼수있는 l-th step user의 representation은 다음과 같다.
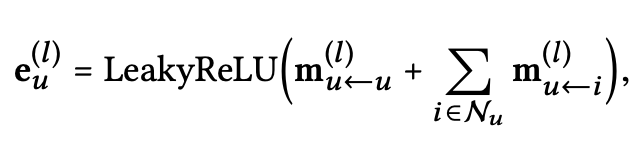
l-th step에서 propagate된 메시지들은 다음과 같이 정의된다.
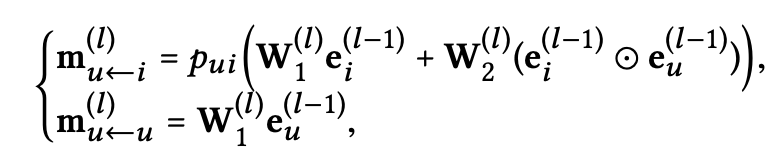
- $W_1^{(l)},W_2^{(l)} \in R^{d_lXd_{l-1}}$: trainable transformation matrix들이고, $d_l$은 transformation size를 의미한다.
- $e_i^{(l-1)}$: previous message-passing step에서 생성된 item representation을 의미하고, (l-1) hop neighbor에서의 message를 저장하고 있다. 이것은 layer l에서 user u의 representation에 기여한다.
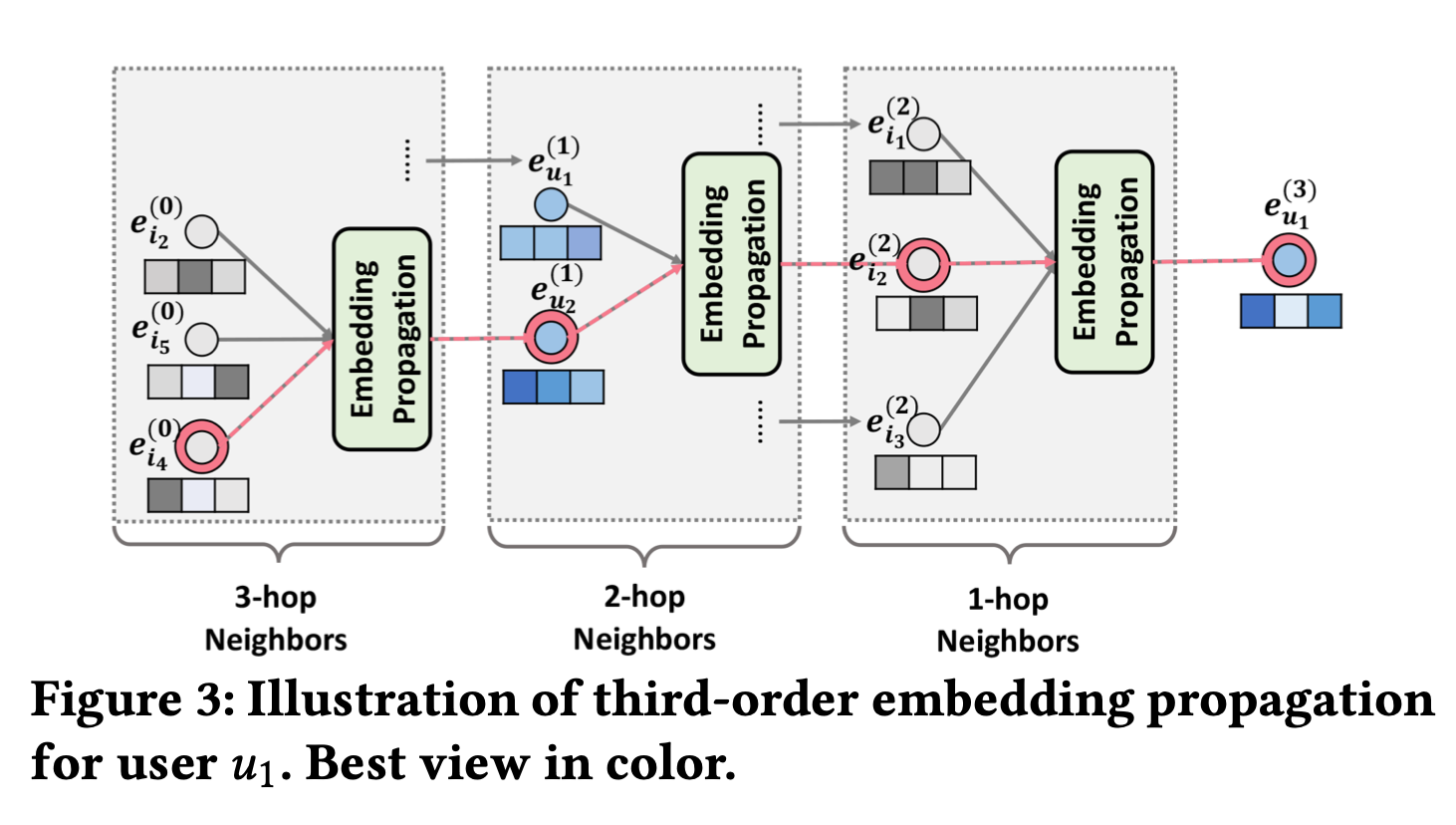
Figure 3에서는 embedding propagation process에서
u1 ← i2 ← u2 ← i4와 같은 collaborative signal을 보여준다. $i_4$에서의 message가 explicit하게 $e_{u_1}$에 encode된다. 그래서 multiple embedding propagation layer를 쌓는 것을 통해 collaborative signal을 representation learning process안으로 넣어준다.
Propagation Rule in Matrix Form: embedding propagation의 전체 view와 batch implementation을 이용하기 위해, 다음과 같이 layer-wise propagation rule 에 대한 matrix form을 제시한다.
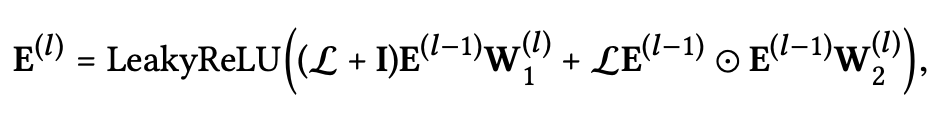
- $E^{(l)}\in R^{(N+M)Xd_l}$: l step의 embedding propagation 이후에 얻은 users와 items의 representation을 의미한다.
- $E^{(0)}$: 처음 message-passing iteration에서의 set $E$을 의미한다. $e_u^{(0)}=e_u, e_i^{(0)}=e_i,I=identity\space matrix$
- $L$: Laplacian matrix for user-item graph.
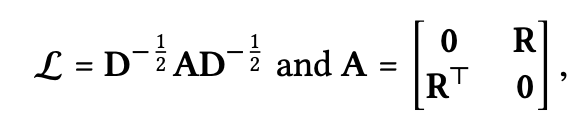
- $R\in R^{NXM}$: user-item interaction matrix.
- $A$: adjacency matrix
- $D$: diagonal degree matrix
- t-th diagonal element $D_{tt}=\mid N_t\mid$
- nonzero off-diagonal entry $L_{ui}=1/\sqrt{\mid N_u \mid \mid N_i \mid}$ (equal to $p_{ui}$
matrix-form propagation rule을 구현함으로써, 모든 user와 모든 item들의 representation을 동시에 효율적인 방법으로 update시킨다. large-scale graph에서 graph convolution network을 동작가능하게 해주는 node sampling 과정을 거치지 않게해준다.
2.3 Model Prediction
L layer propagate한 이후에, user u에 대한 multiple representation ${e_u^{(1)},….,e_u^{(L)}}$을 얻는다. 각기 다른 layer에서 얻은 representation들은 다른 connection을 통한 메시지를 강조하므로, user preference에 대해 각각 다른 contribution을 갖는다. 그러므로 이것들을 concatenate하여 user를 위한 final embedding을 구성한다. (item에도 같은 연산을 한다.)
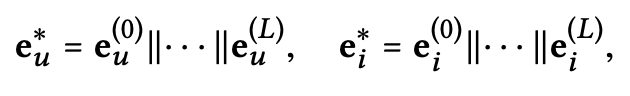
이렇게 함으로써, embedding propagation layer로 initial embedding에 대해 충분한 정보를 주었을 뿐만 아니라, $L$를 조절하여 propagation 범위를 제어할 수 있게 된다.
concatenation 말고도, 다른 aggregator들은 또한 적용될 수 있다. ex) weighted average, max pooling, LSTM, etc. 다른 순서로 connectivities를 합치는 각기 다른 aggreagator를 의미한다.
이러한 concatenation의 이점은 단순함에 있다, 추가적으로 학습되는 파라미터가 없고, layer-aggregation 메커니즘이라 불리는 GNN의 최신 work에서 꽤 효율적인 것으로 밝혀졌다.
마지막으로 target item에 대한 user의 preference선호도를 estimate하기 위해 inner product한다.
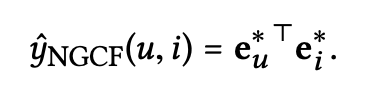
이 논문에서는 embedding function을 강조하기 위해 inner product을 사용하여 단순한 interaction function을 사용한다. (NN기반 interaction function은 future work에 남겨둠)
2.4 Optimization
model parameter들을 학습하기 위해서, 추천시스템에서 많이 사용되는 pairwise BPR loss를 사용한다. BPR loss는 observed, unobserved user-item interaction에 대해서 상대적인 순서를 고려한다. 특히, BPR은 user의 선호를 많이 반영한 observed interaction들에 대해 unobserved interaction보다 더 높은 prediction을 한다. objective function은 다음과 같다.
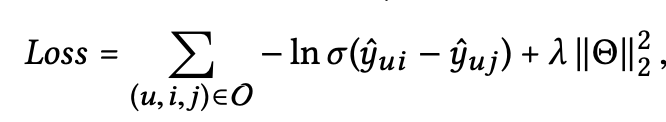
- $O=({(u,i,j) \mid (u,i)\in R^+,(u,j)\in R^-})$: pair wise training data
- $R^+$: observed interation
- $R^-$: unobserved interaction
- $\sigma(.)$: sigmoid function
- $\theta =(E,(W^{(l)}_1, W^{(l)}_2 ) _{l=1}^L )$ : all trainable model parameters
- $\lambda$ control $L_2$ regularization. (prevent overfitting)
그리고 mini-batch Adam을 사용하여 prediction model을 optimazation하고 model parameter들을 업데이트 시킨다. 특히, 랜덤하게 샘플된 triples $(u,i,j)\in O$에 대해서, 이것들의 representation $[e^(0),…,e^(L)]$을 L step의 propagation이후에 정하고, lossfunction의 gradient를 사용하여 model parameter들을 update시킨다.
2.4.1 Model Size
NGCF는 각 propagation layer l에서 embedding matrix $E^{(l)}$을 얻지만, two weight matrix로 이루어진 $d_l X d_{l-1}$의 매우 적은 파라미터만 소개되었다. 이런 embedding matrix들은 user-item graph structure와 weight matrix에 기저한 transformation과 함께 embedding look-up table $E^{(0)}$에서부터 derived되었다. MF와 비교해보았을때, NGCF는 훨씬 적은 $2Ld_ld_{l-1}$의 parameters만 사용한다. (다른 추가적인 파라미터는 무시해도된다.) L은 보통 5보다 작고, user,item의 수보다 작은 $d_l$은 embedding size이다.
예를들어 비교해 보겠다. 본 논문에서 사용한 데이터셋 중 하나인 Gowalla dataset (20K users, 40K items)을 사용한다 해보자. embedding size는 64이고, 3 propagation layer의 size는 64x64일때, MF는 4.5M 개수의 파라미터를 갖는 반면, NGCF는 0.024M개의 파라미터를 갖는다. 요약하면, NGCF는 훨씬 적은 model parameter를 이용하여 high-order connectivity modeling을 구현했다.
2.4.2 Message and Node Dropout
deep learning 모델이 strong representation ability를 갖지만, overfitting으로부터 취약하다. Dropout은 overfitting에 대해 효과적인 solution이다. 이전 work들에 기반하여, NGCF에 두가지 dropout technique을 구현했다. (1) message dropout (2) node dropout.
Message dropout은 outgoing message들에 대해 랜덤핳게 drop out시킨다. 특히, 위에서 언급한 $m^{(l)}{u\leftarrow i}=p{ui}(W_l^{(l)}e_i^{(l-1)}+W_2^{(l)}(e_i^{(l-1)}\odot e_u^{(l-1)})$ 식을 통해 propagate된 message들을 $p_1$의 확률로 dropout 시킨다. l-th propagation layer에서, message의 일부부만 representation refine하는것에 contribute하기 때문이다.
또한 node dropout은 랜덤하게 랜덤하게 특정 노드를 막고, 모든 outgoing message들을 버린다. l-th propagation layer에서, 랜덤하게 $Laplacian\space matrix$의 $(M+N)p_2$ node들을 drop시킨다. 여기서 $p_2$는 drop ratio이다.
Dropout은 당연하게, 학습시킬때만 사용하고, test할때는 disable되어야 한다. message dropout은 representation이 user와 item사이의 single connection의 유무에 대해 더 robustness하게 해준다. node dropout은 특정 user와 item의 영향을 줄여준다. 이후 챕터에서 message dropout, node dropout에 대한 impact또한 실험해보았다.
2.5 Discussions
첫번째 subsection에서 NGCF가 어떻게 SVD++을 generalize하는지를 보여주고, 그다음 NGCF의 time complexity를 분석한다.
2.5.1 NGCF Generalize SVD++
SVD++는 high-order propagation layer가 없는 NGCF의 special case로 볼 수 있다. propagation layer에서, transformation matrix와 nonlinear activation function을 disable시켰다. 그래서 $e_u^{(1)},e_i^{(1)}$는 user u와 item i의 final representation으로 다뤄졌다. 이러한 simplified model을 NGCF-SVD라 하고, 다음과 같이 formulate할 수 있다.
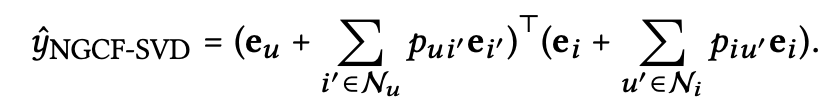
$p_{ui’}=1/\sqrt{\mid N_u\mid}$, $p_{u’i}=0$ 으로 setting하면 SVD++ model로 바꿀 수 있다. FISM이라는 item-based model 또한 NGCF의 special case로, $p_{iu’}=0$인 경우에 해당한다.
2.5.2 Time Complexity Analysis
위에서 설명했다 시피, layer-wise propagation rule이 main operation이다. l-th propagation layer에 대해 matrix multiplication은 $O(\mid R^+\mid d_ld_{l-1})$의 시간복잡도를 갖는다. 여기서 $\mid R^+\mid$ 는 Laplacian matrix에서 nonzero entry의 개수를 나타낸다.
$d_l,d_{l-1}$은 current, previous transformation size를 의미한다. Prediction layer은 inner product으로만 이루어져 있고, training epoch크기의 시간복잡도 $O(\sum_{l=1}^L \mid R^+\mid d_l)$을 갖는다. 그러므로 전체 시간 복잡도는 $O(\mid R^+\mid d_ld_{l-1}+ \sum_{l=1}^L \mid R^+\mid d_l)$이다.
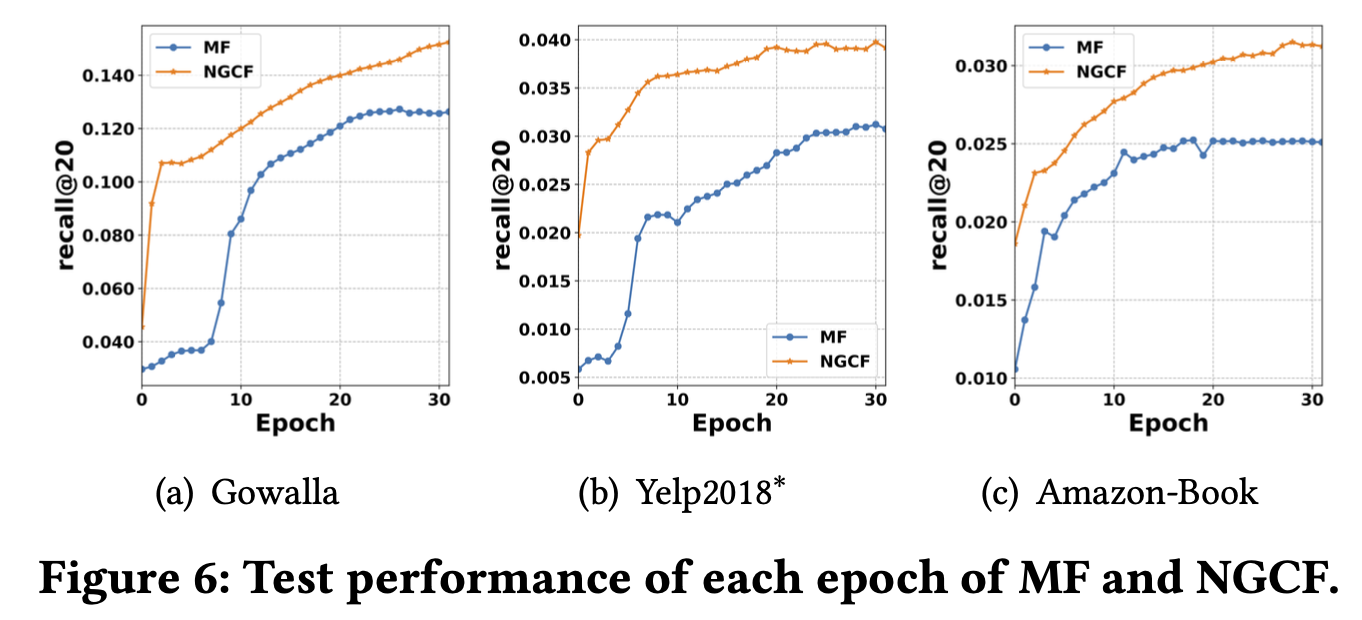
MF와 NGCF 각각에 대해 학습을 시켯을때, epoch당 20초, 80초가 걸렸고, inference(test)할때는 전체 testing instance들에 대해 80s, 260s가 걸렸다.
3. Related Work
NGCF와 관련된 model-based CF, graph-based CF, graph neural network-based method들에 대해 review할 것이다.
3.1 Model-based CF Methods
MF, NeuMF에 대한 이야기로 시작을 해서, 간단하게 설명하고 넘어가겠다. (자세한 내용은 다음 블로그 링크(MF, NeuMF)를 확인) MF은 user-item의 linearity한 relation만 고려하기 때문에, ranking loss가 있었다. NeuMF에서는 이것을 고려하여 non-linearity도 고려했다. 두 모델 외에도 LRML이라는 translation-based CF model도 소개되었다. 이런 딥러닝 모델도 성능이 좋았음에도 불구하고, design of embedding function은 CF signal은 implicitly capture되기 때문에 optimal CF embedding을 구성하기엔 불충분했다.
요약하면, embedding function은 descriptive feature들을 vector로 변환했고, interaction function들은 vector들에 대한 similarity를 측정했다. 이것들을 사용하여 the transitivity property of behavior similarity를 capture할 수 있었지만, explicit하게 encode하지 못했고, 그래서 embedding space에서 위치한 간접적으로 연결된 users,items close relation이라는 것을 보장하지 못했다. Explicit encoded CF signal없이는 desired property를 갖는 embedding을 얻기 어렵다.
3.2 Graph-Based CF Methods
user-item interaction graph로 user inference를 설명하기 위한 work들에 대해 설명하겠다. 초기에는 idea of label propagation을 사용하여 CF effect을 capture했다. 사실 이 방법은 historical items과 target item에 근거하여 recommendation score를 계산하므로 neighbor-based methods의 한 종류이다. objective function을 최적화 하기 위한 model parameter들이 없었기 때문에 model-based CF 방법들보다 성능이 떨어졌다.
최근에 제안된 method인 HOP-Rec은 embedding-based method와 graph-based method를 합쳐서 이 문제점을 완화시켰다. 한 user에 대해서 multi-hop connected item들의 interaction 정보를 얻기 위해 random walk으로 시작하여, 여기서 얻은 interaction 정보를 이용하여 BPR을 이용하여 MF를 학습시켰다. HOP-Rec은 connectivity 정보를 제공하기 때문에 단순히 embedding만 사용하는 MF보다 성능이 더 좋았다. 하지만 High-order connectivity를 사용하는게 아니라 connectivity 정보를 training data 추가하는 것이었다. 또한 HOP-Rec의 성능은 random walk에 dependent하므로, 많은 tuning effort가 필요했다.
3.3 Graph Convolutional Networks
specialized graph convolution operation을 user-item interaction graph에 사용하여 NGCF를 더 효과적으로 만들었다. 이 연산을 이용해 CF signal을 high-order connectivity에 사용할 수 있게 했다. 다음 내용은 GCN을 추천시스템에 사용한 세개의 모델에 대한 내용이다.
- GC-MC: user와 item사이에서 direct connection을 사용하기 위해 one convolutional layer만 사용했고, high-order connectivity에서의 CF signal을 얻지 못했다.
- PinSage: item-item graph for Pinterest image recommendation에서 사용하는 multiple graph convolution이다. user behavior가 아닌 level of item relation을 capture했다.
- SpectralCF: spectral domain에서의 user와 item사이의 가능한 모든 connectivity를 spectral convolution operation을 이용해 발견했다. eigen-decomposition을 통해 이 관계를 discover할 수 있는데, eigen-decomposition은 매운 시간복잡도가 크고, large-scale recommendation 시나리오를 support하기 어렵다.
4. Experiments
- RQ1: How does NGCF perform as compared with state-of-the-art CF methods?
- RQ2: How do different hyper-parameter settings (e.g., depth of layer, embedding propagation layer, layer-aggregation mechanism, message dropout, and node dropout) affect NGCF?
- RQ3: How do the representations benefit from the high-order connectivity?
4.1 Dataset Description
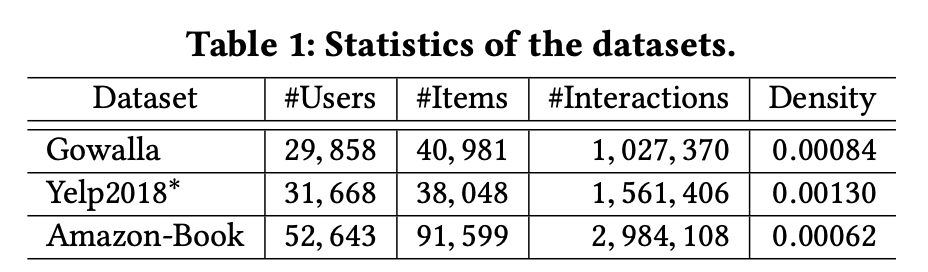
- Gowalla
- Yelp2018
- Amazon-book
4.2 Experimental Settings
4.2.1 Evaluation Metrics
user와 interact하지 않은 모든 item들을 negative item을로 보았다. 모델들은 training set에서 사용했던 positive item을 제외한 모든 item에 대한 각 user의 선호도를 출력했다. top-K recommendation, preference ranking을 효과적으로 평가하기 위해서 recall@K and ndcg@$K^3$를 사용했다. default K=20을 사용한다.
4.2.2 Baselines
- MF
- NeuMF
- CMN
- HOP-Rec
- PinSage
- GC-MC
4.2.3 Parameter Settings
- Embedding size : 64
- grid search for hyper parameter
- learning rate = {0.0001, 0.0005, 0.001, 0.005} tuned
- coefficient of L2 normalization: {0.0, 0.1, · · · , 0.8} tuned
- node dropout ratio: {0.0, 0.1, · · · , 0.8} tuned.
- model parameters : Xavier initializer
- early stopping strategy performed. premature stopping if recall@20 on the validation data does not increase for 50 successive epochs.
- NGCF L : 3. (to model the CF signal encoded in third- order connectivity)
- NGCF의 three embedding propagation layers에 대해 node dropout ratio of 0.0, and message dropout ratio of 0.1 사용.
4.3 Performance Comparison (RQ1)
4.3.1 Overall Comparison
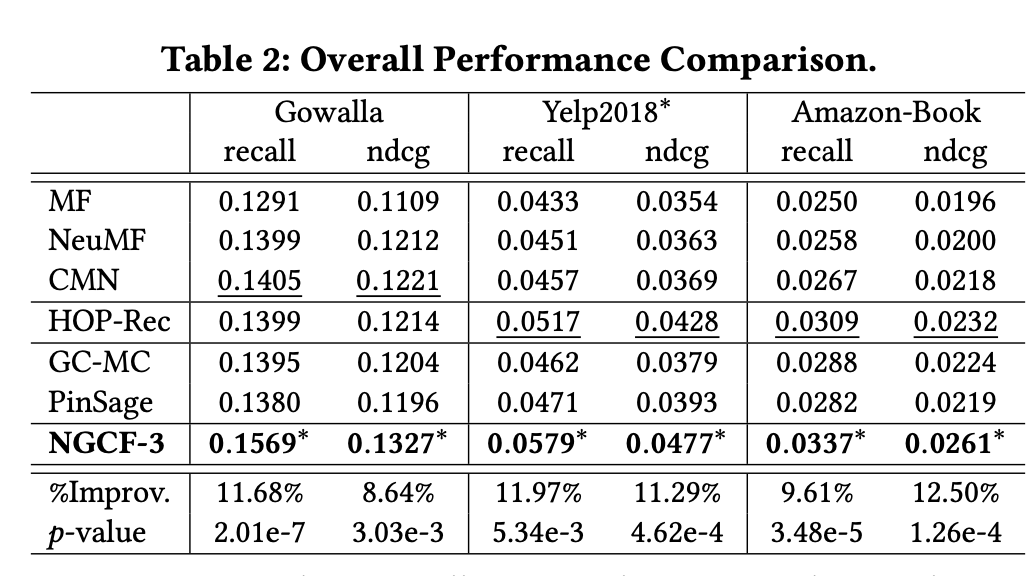
4.3.2 Performance Comparison w.r.t. Interaction Sparsity Levels.
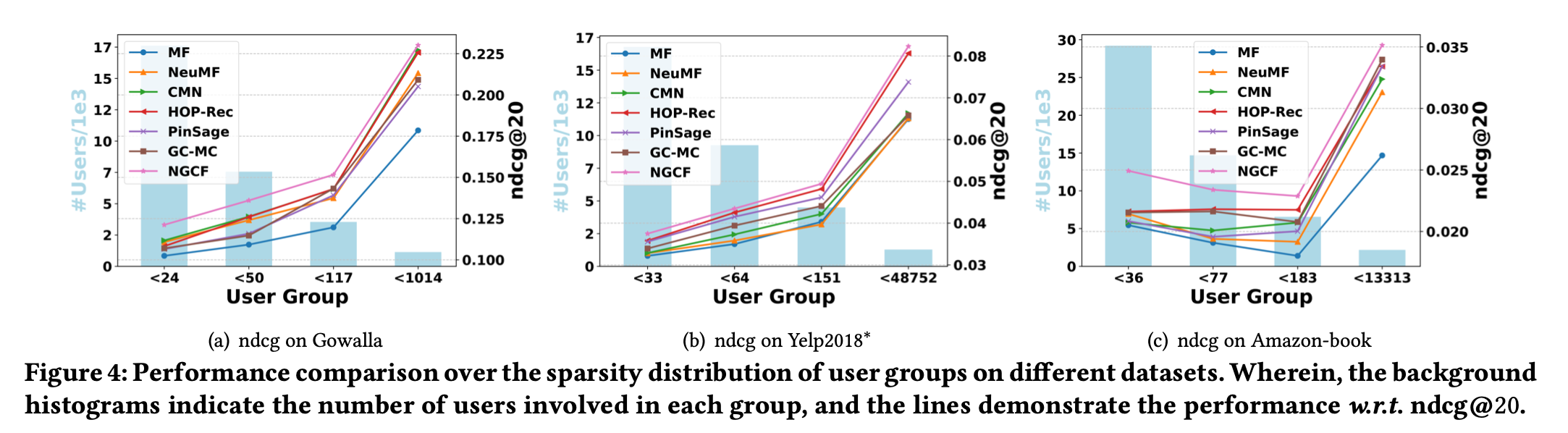
4.4 Study of NGCF (RQ2)
4.4.1 Effect of Layer Numbers
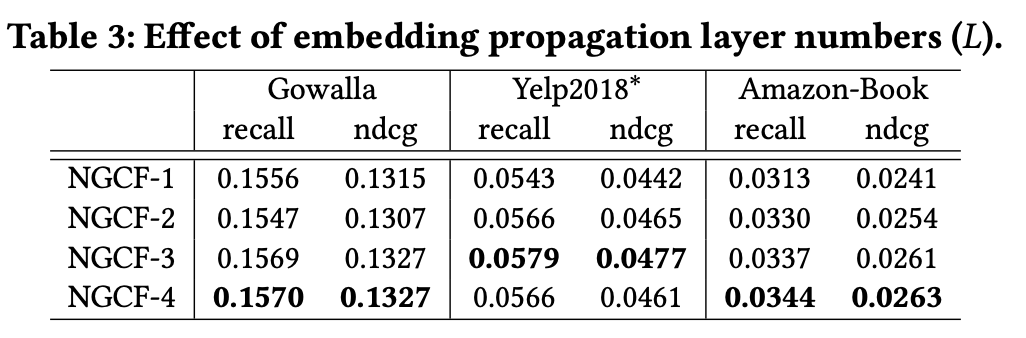
4.4.2 Effect of Embedding Propagation Layer and Layer- Aggregation Mechanism.
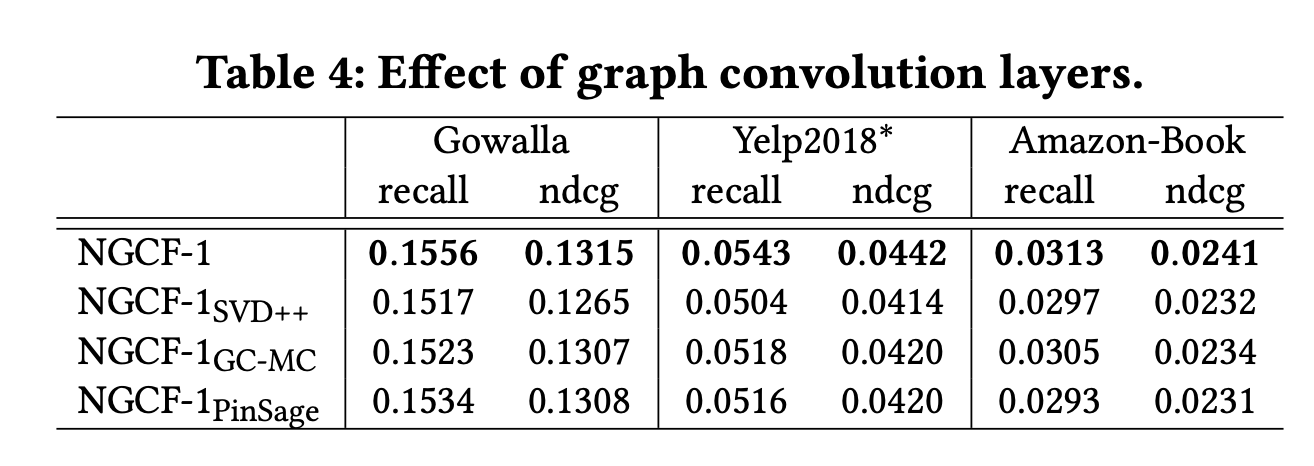
4.4.3 Effect of Dropout
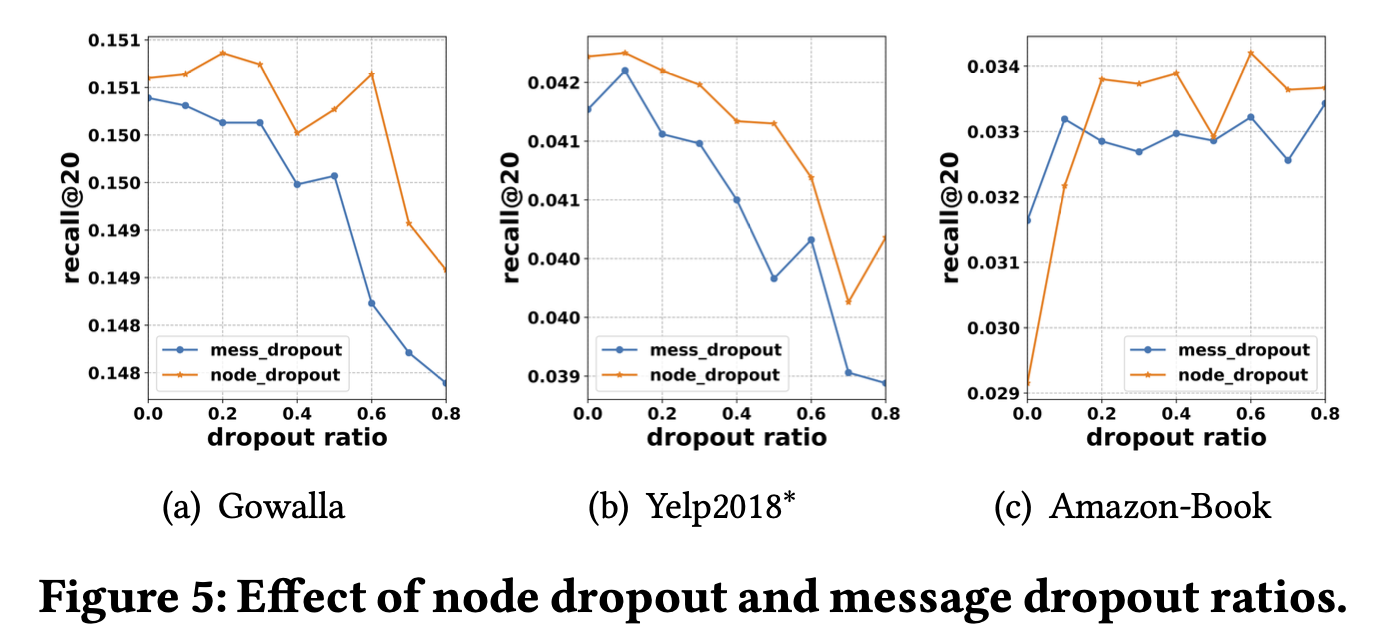
4.4.4 Test Performance w.r.t. Epoch
4.5 Effect of High-order Connectivity (RQ3)
