Neural Collaborative Filtering (WWW 2017)

28 Dec 2021

2017년에 발표된 Neural Collaborative Filtering 논문을 review한 내용입니다. Matrix Factorization에 대해서는 한계를 다룬 내용을 제외한 것은 생략하겠습니다. (다음 포스트를 참고하면됩니다.)

NCF에서 제가 생각한 핵심은 다음과 같습니다.

기존의 Matrix Factorization의 한계점은 user-item의 interaction을 linear한 방식(fixed dot product)으로 계산하기 때문에, ranking loss가 생긴다. latent factor들을 latent space에서 표현했을때, cosine similarity가 실제 matrix의 factor의 양상과 일치하지 않는것을 확인할수 있다.
user-item의 interaction에 대해서 non-linear한 방식으로도 학습하기 위해 MLP를 추가했고, 기존의 MF의 linear한 factor도 사용하기 위해 GMF(Generalized Matrix Factorization)를 MLP와 concatenate하여 NeuMF를 만들었다.
이때, 새로 배운점은 MLP, GMF를 concatenate하면 objective function이 non-convex하기 때문에 local optima로 optimize된다는 것이었다. 그래서 이 논문에서는 pre-trained MLP, pre-trained GMF를 이용하여 마지막 output layer만을 SGD를 통해 optimize한다. (MLP, GMF는 Adam optimizer로 optimize한다. NeuMF에서 Adam을 사용하지 못하는 이유는 pre-trained model을 사용하므로 momentum에 대한 정보가 없기 때문이다.)
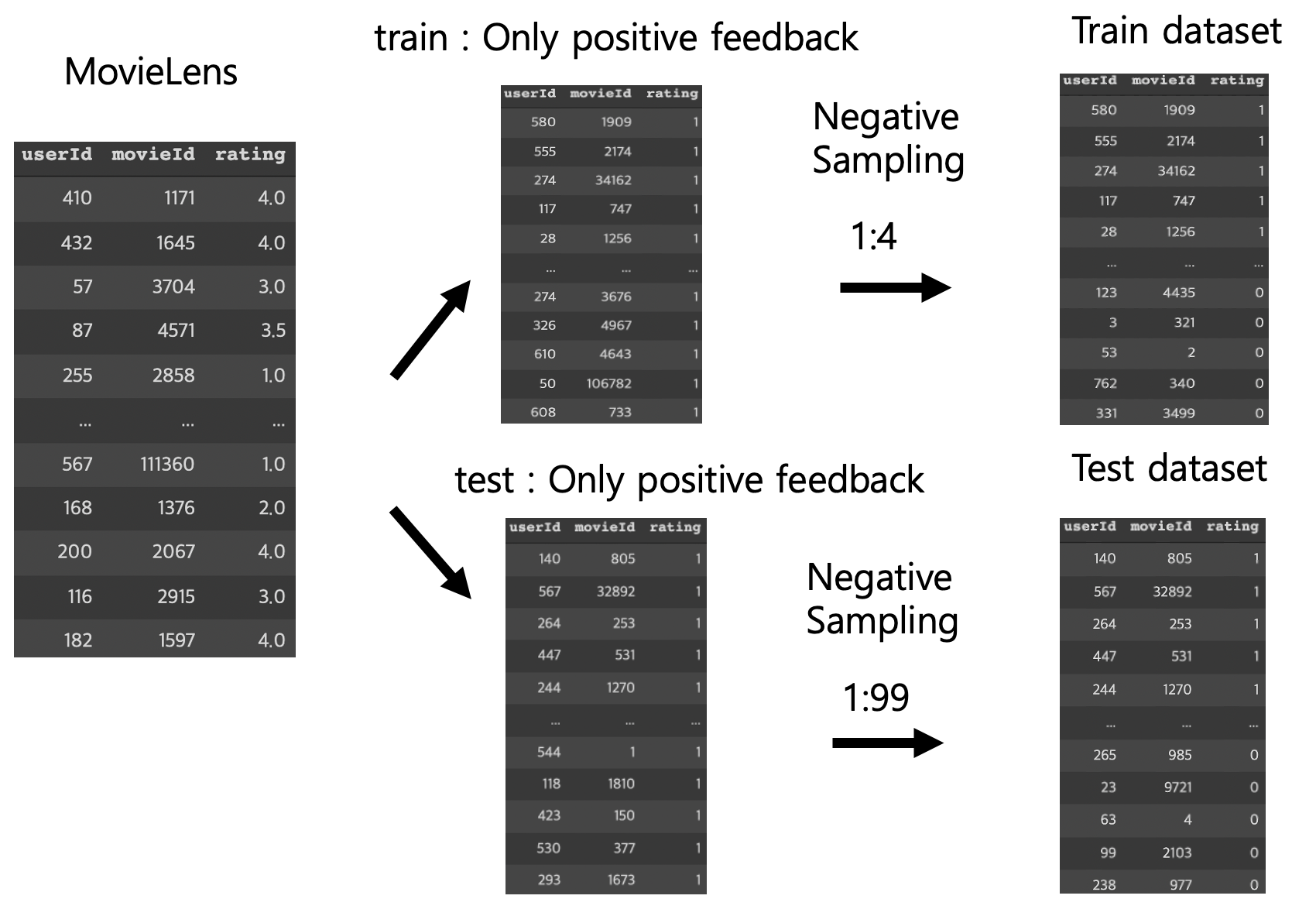
다음은 dataset이 어떻게 구성되어있는지에 대한 내용이다. 대부분의 내용이 논문에는 명시되어 있지 않고, 저자의 code에 이렇게 구현되있을뿐, 납득되지 않는 부분도 존재한다. 하지만 모델의 성능을 비교하기 위해 저자와 최대한 같은 데이터 셋을 구성하려고 노력했다. 현재 주어진 dataset에는 user와 item의 interaction이 있는 positive feedback만 있다. MovieLens Dataset은 user-based dataset으로, 최소 20개의 movie를 rating한 user에 대한 데이터로 이뤄져있다. 예를들어 user A에 대해서 trainset과 testset을 나눈다고 했을때, user A의 rating data중 하나만 testset으로 할당하고, user A의 나머지 rating data는 trainset으로 할당하였다. 이렇게 한 이유는 testset으로 평가 지표를 계산할때, 특정 user의 데이터만 많아지게 되면 계산값이 특정 user에 대해 편향 될수 있기 때문이다.
그다음 trainset에 대해 implicit feedback을 만들기 위해, 나누기전의 전체 rating data를 참고하여, user A가 평가하지 않은 movie들로 1개의 positive sample당 4개의 negative sample을 만든다. 이제 user A에 대한 testset을 만들어보자. HR@k, NDCG@k에서 k가 어떤 값이 될지 모르므로 충분히 많은 데이터를 토대로 하나의 user에 대해 예측을 해야한다. 현재 user A에 대해서는 한쌍의 dataset 밖이 없다. 1개의 positive sample당 99개의 negative sample을 만든다. 왜 99개로 negative sampling하는지 살펴보자. 앞서 trainset에서 user A에 대해 rating한 movie가 최소 19개가 있다고 했었는데, 이것을 20개라고해보자. 그러면 negative sampling한 후에 trainset과 testset에서 user A의 data 비율이 대략 100:100이 된다. (왜 100:100을 맞췄는지는 충분히 납득가지 않는다. 보통 추천시스템에서 dataset 구성하는 convention일거라 생각한다.)

현재 NFCML repository에 해당 논문을 구현해보고 있습니다.

Abstract

implicit feedback 데이터셋을 기반으로 하여 recommender system의 collaborative filtering이라는 key problem에 대해 deep learning을 사용한 기술을 개발했다. recommender system에 deep learning을 사용한 기존의 work들은 item에 대한 textual description 혹은 acoustic feature of music과 같은 model auxiliary information에만 사용했다. 그 work들은 latent feature에 대해 Matrix Factorization의 inner product에만 의존한다. Matrix Factorization의 inner product를 데이터로부터의 non linear한 arbitrary function을 학습할 수있는 신경만 구조로 대체하는 Neural network- based Collaborative Filtering(NCF)를 제안한다. NCF는 generic하고, NCF의 framework안에서 Matrix Factorization을 설명하고 generalize할수 있다. 추가로, Two real-world dataset을 이용하여 NCF를 향상시키는 SOTA한 방법을 사용한다. Empirical evidence는 deeper layers of neural networks를 사용하는 것이 더 좋은 recommendation performance을 보여준다.

1. INTRODUCTION

이 논문은 watching videos의 유무, purchasing products의 유무 또는 clicking items과 같이 간접적으로 사용자의 선호도를 반영하는 implicit feedback에 focus를 맞춘다. Explicit feedback (rating, 선호도와 같은)보다 implicit feedback이 track하기 쉽고, content provider로 부터 더 쉽게 collect할 수 있다. 하지만 사용하기엔 더어렵다 왜냐하면 user satisfaction이 관찰되지 않았고, negative feedback에 대한 natural scarcity가 존재하기 때문이다. 이 논문의 main contribution은 다음과 같다.

users와 items의 latent feature를 model하고, neural network에 기반한 collaborative filtering을 general한 NCF framework을 고안하기 위한 신경망 구조를 제시한다.
MF는 NCF의 specialization으로 해석될 수 있고, NCF를 high level of non-linearities으로 모델링 하기 위해 multi-layer perceptron을 사용한다.
Effectiveness of our NCF approaches와 the promise of deep learning for collaborative filtering을 증명하기 위해 두가지 real world dataset을 사용한다.

2. PRELIMINARIES

문제를 먼저 formalize하고나, collaborative filtering with implicit feedback에 대한 해결책을 애기하겠다. 그 다음 MF에서의 inner product을 사용하는것의 한계에 대해 설명한다.

2.1 Learning from Implicit Data

$M$ : number of users , $N$ : number of items 이라고 하자. user의 implicit feedback으로 user-item interaction matrix $Y ∈ R^{M×N}$ 을 정의할것이다. 이때 matrix $Y$의 각 원소 $y_{ui}$는 다음과 같다.

$y_{ui} = 1$ if interaction (user u, item i) is observed. otherwise $y_{ui}$ = 0.

이때 $y_{ui}$이 1과 0일때의 의미는 다음과 같다. $y_{ui}$ = 1 은 interaction between user and item을 의미한다. 하지만 이것이 user u가 item i를 좋아하는 뜻은 아니다. 비슷하게 $y_{ui}$=0은 user u가 item i를 싫어한다는 의미가 아니며, 단지 user가 item을 알지 못한다는 것을 의미한다.

Implicit data로 부터 학습 것이 challenging한 이유는 user’s preference에 대해 noisy signal만을 제공하기 때문이다. observed entry들은 item에대한 흥미 만을 나타내는 반면, unobserved entry들은 missing data라는 것만을 의미한다. implicit feedback의 recommender system은 item들을 ranking하는 데에 사용할 unobserved entry Y의 score를 예측하는 문제로 formulate 되어 진다. $\hat y_{ui} = f (u, i\mid\theta)$ 를 학습하는 것으로 추상화될 수 있다. 여기서 $\hat y_{ui}$는 predicted score of interaction $y_{ui}$를 의미하고, $\theta$는 model parameters를 의미하고, $f$는 model parameter를 predicted score에 mapping하는 함수를 의미한다. parameter $\theta$를 estimate하기 위해 objective function을 최적화할때 주로 사용하는 ml paradigm을 사용한다. 주로 사용하는 두가지 objective function은 (1) pointwise loss와 (2) pairwise loss가 있다.

pointwise loss: explicit feedback에 대한 많은 work에서 point wise learning은 주로 $\hat y_{ui}$와 target value $y_{ui}$의 squared loss를 최소화 하는 regression framework을 따른다. negative data를 다루기 위해선, 모든 unobserved entry등를 negative feedback으로 거나, unobserved entry로부터 negative instance를 sample 하여 다뤄야 한다.
pairwise loss : pairwise learning에서는 observed된 것이 unobserved 된것 보다 더 높은 rank를 받아야 한다. $\hat y_{ui}$와 target value $y_{ui}$의 loss를 최소화 하는 것 대신, pairwise learning에서는 observed entry $\hat y_{ui}$와 unobserved entry $y_{ui}$사이의 margin을 최대화 하게 학습한다.

NCF framework에서는 pointwise, pairwise learning을 모두 support한다. 뒤의 내용에 나오겠지만, pure model에 집중한 논문이기 때문에 pointwise learning을 사용할 것이라고 한다.

2.2 Matrix Factorization의 한계

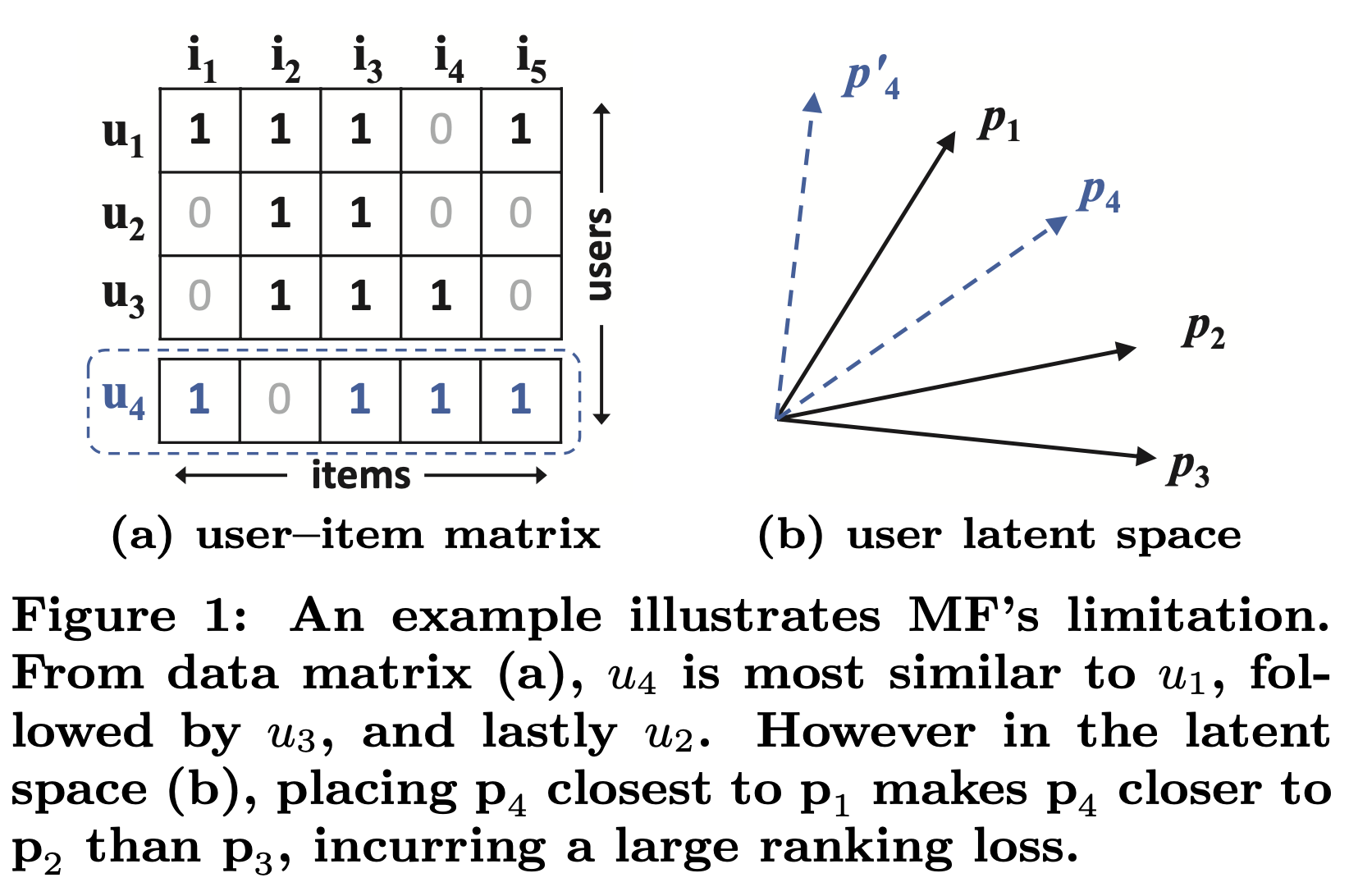
위의 그림은 어떻게 inner product function이 MF의 expressiveness를 제한할 수 있는지 설명한다. 위 그림을 설명하기 앞서 두가지 가정이 필요하다. 첫번째로, MF가 users와 items를 same latent space에 map하기 때문에, 두명의 user사이의 similarity 또한 inner product measure될 수 있고, 각 latent vector사이의 각의 cosine값을 의미한다. 두번째로, generality의 대해 loss없게 하기위해, MF가 recover되기 위해 필요한 ground truth similarity of two user로써 Jaccard coefficient를 사용한다.

Fig 1 (a)의 세번째 row까지 살펴보자. $s_{23}$(0.66) > $s_{12}$(0.5) > $s_{13}$(0.4)임을 쉽게 관찰 할 수 있다. 그리고 latent space에서의 $p_1,p_2,p_3$ vector의 geometric relation들 또한 fig (b)에 plot해 두었다. 이제 새로운 user $u_4$를 고려해보자. $s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)$임을 관찰할 수 있고, u4가 u1과 가장 similar하고, 그다음 u3, u2 순인 것을 의미한다. 하지만 MF model은 $p_4$를 $p_1$과 가장 가깝게 위치시키고, 그다음 $p_2,p_3$ 순을로 가깝다. 즉, large ranking loss가 발생한다.

위의 예시는 MF를 simple and fixed product to estimate complex user item interaction in the low dimensional latent space으로 사용할때 발생하는 possible limitation이다. large latent factor K를 사용하면 이 문제를 해결할수 있지만, 그것은 model의 generalization을 손상시킬 것이다. (sparse한 matrix에서는 더욱이) 이 논문에서는 data로부터 DNN을 사용해 interaction function을 학습시키는 것을 이용하여 위에서 언급한 limitation을 다룬다.

3. Neural Collaborative Filtering

우리는 먼저 implicit한 data를 binary property를 강조하는 probabilistic model인 NCF를 어떻게 학습하는지에 대한 NCF framework을 설명할것이다. 그다음 NCF에서 MF가 어떻게 표현될 수 있는지 보일 것이다. collaborative filtering을 위한 DNN을 설명하기 위해, user-item interaction function을 학습할 MLP를 사용하여 NCF의 예시를 들것이다. 마지막으로 NCF framework아래서 MF와 MLP를 ensemble하는 새로운 neural matrix factorization model을 설명할 것이다. MF의 linearity와 MLP의 non-linearity의 강점을 모두 갖게 된다.

3.1 General Framework

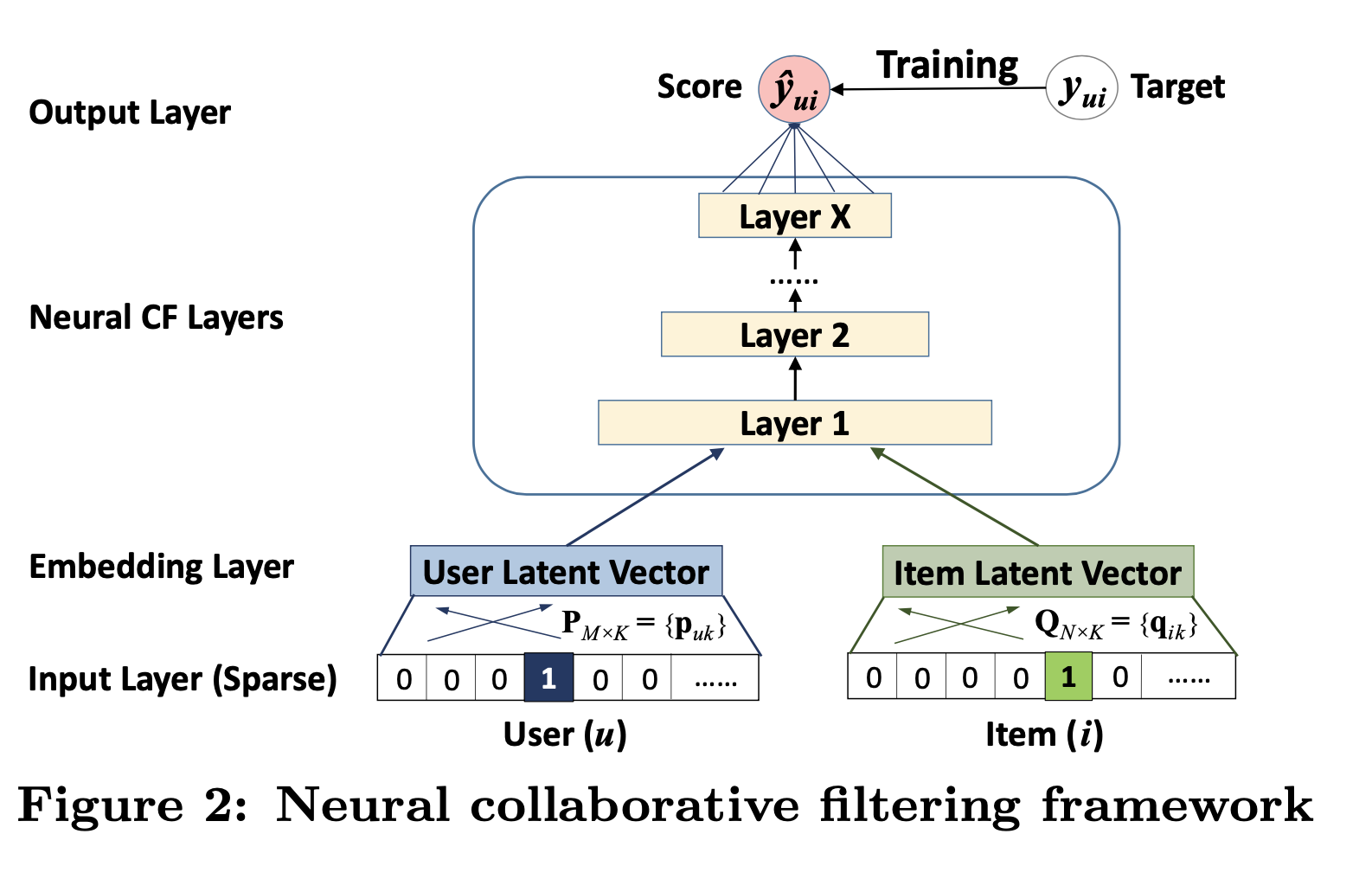
collaborative filtering에 대한 full neural treatment를 다루기 위해, fig2와 같이 user-item interaction $y_{ui}$를 model하기 위해 multi-layer를 적용했다. bottom input layer는 user u와 item i를 describe하는 두가지 feature $v_u^{U}$와 $v_i^{I}$로 구성되고, 이것들은 content-based, neighbor-based와 같은 방식으로 customize될 수 있다.

이 논문은 pure collaborative filtering setting을 다루기 때문에, identity of user and item을 input feature로만 사용할것이고, one-hot encoding된 binarized sparse vector로 transform하여 사용할 것이다. 이러한 input의 generic feature representation에 대해, 이 논문에서 다루는 방법은 user, item을 나타내기 위해 content feature를 사용함으로써 cold-start problem도 쉽게 다룰 수 있다.

input layer위에 embedding layer가 있다. embedding layer는 sparse한 representation을 dense vector에 project하는 fully connected layer이다. The obtained user/item embedding은 latent factor model에서의 context에서 user/item를 위한 latent vector라 할수 있다. user embedding과 item embedding은 latent vector를 prediction score에 맵핑하기 위한 Neural Collaborative Filter layer라 부르는 multi-layer neural architecture에 feed된다. Neural CF layer의 각 layer들은 user-item interaction에 대한 certainLatent structure으로 커스톰될 수 있다. 마지막 hidden layer X는 model의 capability를 의미한다. 마지막 output layer는 predicted score인 $\hat y_{ui}$이고, $\hat y_{ui}$와 target value $y_{ui}$의 pointwise loss를 최소화 하는 방향으로 학습된다.

다른방법으로, Bayesian Personalized Ranking, margin-based loss와 같은 pairwise learning으로도 학습 할수 있다. 이 논문은 neural network modeling part에 초점을 맞추기때문에, pairwise learning은 future work로 미룰것이다.이제 NCF’s predictive model를 다음과 같이 formulate할 수 있다.

predictive model: $\hat y_{ui} = f(P^Tv_u^U,Q^Tv_i^T\mid P,Q,\theta_f)$
$P ∈ R^{M×K}, \space Q ∈ R^{N×K}$ : 각각 user와 item을 위한 latent factor을 의미한다.
$\theta_f$ : function f의 parameter of interaction을 의미한다.
multi-layer neural network인 function $f$: $f(P^Tv_u^U,Q^Tv_i^I) = \phi_{out}(\phi_X(…\phi_2(\phi_1(P^Tv_u^U,Q^Tv_i^I))…))$, $\phi_{out},\phi_{x}$는 output layer와 x-th ncf layer의 mapping function을 의미한다.

3.1.1 Learning NCF

model parameter를 학습하기 위해, point wise method는 squared loss를 사용한 regression을 사용한다.

$L_{sqr}=\sum\limits_{(u,i)\in y\cup y^-} w_{ui}(y_{ui}-\hat y_{ui})^2$ : y는 observed interaction in Y, $y^-$는 unobserved interaction을 의미하는 negative instance를 의미한다. 그리고 $w_{ui}$는 weight of training instance를 의미하는 hyperparameter를 의미한다.

observation이 Gaussian distribution으로부터 generate되었다고 가정한다면 squared loss는 설명될 수 있지만, implicit data에 대해서는 그렇지 않다. implicit data 때문에 target value $y_{ui}$는 1 또는 0으로 binary화 될수있고, 우리는 implicit data의 binary property에 강조를 한 pointwise NCF를 학습하는데 있어 probabilistic한 접근을 제시한다.

implicit feedback의 한가지 class만을 고려해보면, $y_{ui}$ =1은 item i가 user u와 연관되어 있다는 것을 의미하고, 0은 그렇지 않다는 것을 의미한다. prediction score인 $\hat y_{ui}$는 i가 u와 얼마나 연관되어 있는지를 의미한다. NCF에 대해 probabilistic한 설명을 하기 위해, $\hat y_{ui}$를 [0,1]사이로 범위를 제한할 필요가 있다. 이는 logistic, probit function과 같은 probabilistic function을 $\phi_{out}$을 위한 activation으로 사용하면 쉽게 achieve할 수있다. 앞서 말한것에 대해 Likelihood function을 다음과 같이 적을 수 있다.

$p(y,y^{-}\mid P,Q,\theta_f)=\prod\limits_{(u,i)\in y}\hat y_{ui} \prod\limits_{(u,j)\in y^-} (1-\hat y_{uj})$ negative logarithm of likelihood를 이용하여 위의 식에 대입하면 다음과 같다.
$L = -\sum\limits_{(u,i)\in y}log\hat y_{ui} -\sum\limits_{(u,j)\in y^-}log(1-\hat y_{uj}) = -\sum\limits_{(u,i)\in y\cup y^-}y_{ui}log\hat y_{ui}+(1-y_{ui})log(1-\hat y_{ui})$

SGD를 통해 위의 objective function을 최소화 할수 있다. 위의 식은 binary-cross-entropy식과 같고, log loss로 알려져있다. NCF에 대해 probabilistic하게 다루는것에 의해, implicit feedback을 binary classification problem으로 다룰 수 있다. recommendation literature에서 classification-aware log loss가 거의 다뤄저지지 않아서 그것의 effectiveness에 대해 4.3절에서 다뤘다.

3.2 Generalized Matrix Factorization (GMF)

MF가 어떻게 NCF framework의 special case로 interpret될 수 있는지 설명하겠다. user(item) ID를 one hot encoding했기 때문에, obtained embedding vector는 user (item)의 latent vector로 고려될 수 있다. latent vector $p_u$가 $P^Tv_u^U$, item latent vector $q_i$가 $Q^Tv_i^I$라 하자.

NCF의 첫번째 layer는 다음과 같이 정의할 수 있다.

$\phi_1 (p_u,q_i)=p_u\odot q_i$

NCF의 마지막 layer는 다음과 같이 정의할 수 있다.

$\hat y_{ui}=a_{out}(h^T(p_u\odot q_i))$

$a_{out}$은 activation을 의미하고, $h$는 edge weight of output layer를 의미한다. $a_{out}$에 대해 identity function으로, $h$에 대해 uniform vector of 1로 사용한다면 MF model을 recover할 수 있다. NCF framework하에서, MF는 쉽게 generalized, extended될 수 있다. 만약 $h$를 uniform constraint없이 학습되게 하면, latent dimension에 따라 다르게 중요도를 매기는 변형된 MF가 될것이다. 만약 $a_{out}$에 대해 non-linear를 사용하면, linear MF보다 더 expressive하게 될 것이다. 이 논문에서 $a_{out}$에 대해서는 sigmoid function $1/(1+e^{-x})$을 사용할ㄹ것이다. $logloss(cross-entropy)$로 부터 $h$를 학습하여 사용할것이고, 위의 MF모델을 Genearalized Matrix Factorization(GMF)라 한다.

3.3 Multi-Layer Perceptron(MLP)

NCF는 users,items에 대해 2가지에 대해 modeling을 하는 방법을 사용하기때문에, 이 2가지 feature를 concatenate하는 방법도 intuitive하다. 이러한 구조는 multimodal deep learning work과 같은 곳에 많이 사용한다. 하지만 vector concatenation이 user 와 item latent features간의 어떠한 Interaction도 설명하지 않는다. 그리고 이것은 cf를 모델링하는데에 불충분한다.

그래서 이 문제를 해결하기 위해 standard MLP를 사용하여 interaction between user and item latent features를 학습한다. 이는 또한 model에 large level of flexibility를 부여하고, $p_u,q_i$의 interaction을 학습하기 위해서 GMF에서의 fixed-element-wise product만을 하는것보다 non-linearity를 사용할 수 있게 된다.

NCF하의 MLP는 다음과 같이 정의될 수 있다.

$z_1=\phi_1(p_u,q_i)=[[p_u],[q_i]]$
$\phi_2(z_1)=a_2(W_2^Tz_1+b_2)$,…,
$\phi_L(z_{L-1})=a_L(W_L^Tz_K-1+b_L),$
$\hat y_{ui}=\sigma(h^T\phi_L(z_L-1))$
$W_x, b_x, a_x$ : weight matrix, bias vector, activation function for the x-th layer’s perceptron

$a_x$에 대해 Relu를 사용했고, sparse한 data에 적합하고, 모델을 덜 과적합하게 만든다.

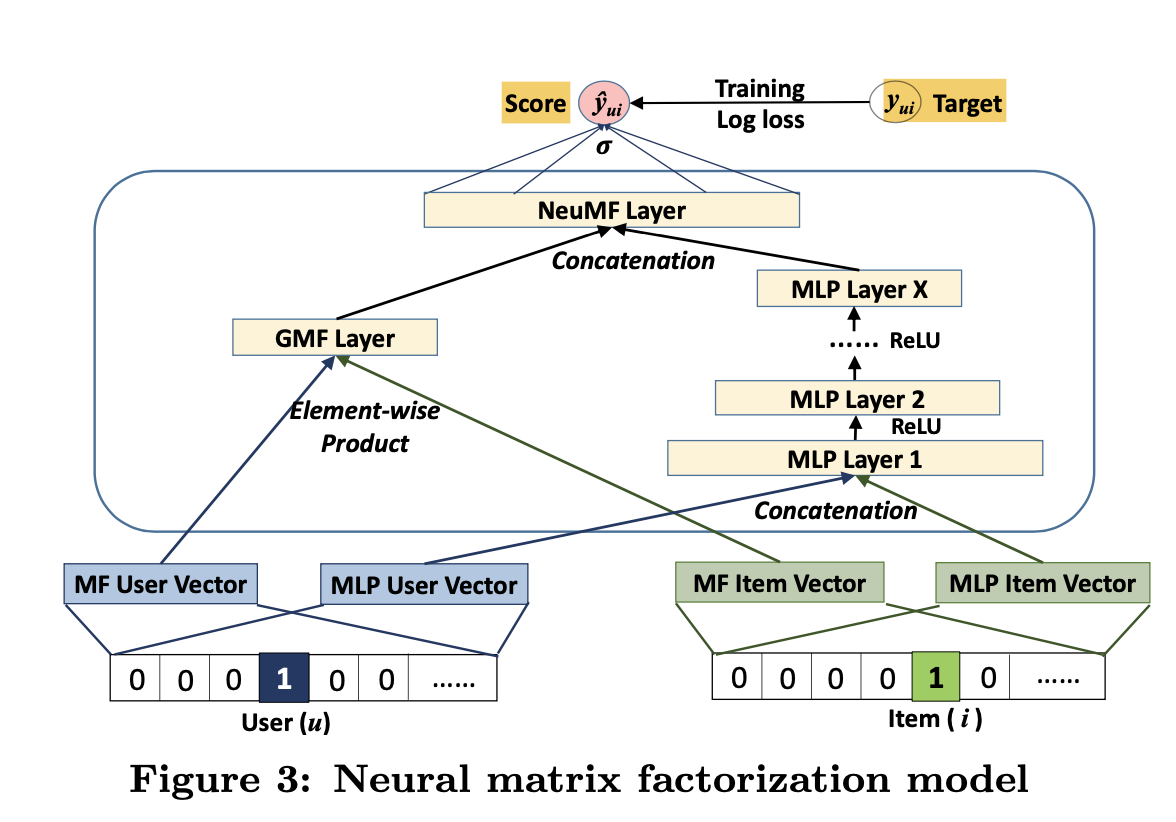
3.4 Fusion of GMF and MLP

NCF - linaer kerenl latent feature for GMF, non linear kernel for MLP를 알아봤다. 이제 NCF하에서 서로를 reinforce하여 복잡한 Interaction에 대한 더 좋은 model을 만들 수 있도록 GMF, MLP를 어떻게 합치는지 알아보자. 간단하게 말하면 다음 두 단계로 이뤄진다.

GMF and MLP share the same embedding layer
combine the outputs of their interaction functions.

이 구조는 Neural Tensor Network (NTN)와 유사하다. model for combining GMF with a one-layer MLP는 다음과 같이 formulate될 수 있다.

$\hat y_{ui}=\sigma(h^Ta(p_u\odot q_i+W[[p_u],[q_i]]+b))$

하지만 GMF,MLP의 embedding을 share하는 것은 fused model의 성능을 저하 시킬 수도 있다. 이렇게 공유하는 방식은 GMF,MLP가 같은 size의 embedding을 사용해야한다. 두개의 모델에 대한optimal한 embedding size은 각각이 매우 다를것이다. 그래서 fused model에 대해 flexibility를 제공하기 위해, GMF와 MLP가 separate embedding을 학습하게 했고, fig3과 같이 마지막 hidden layer를 concatenate함으로써 두개의 모델을 합쳤다. 다음과 같이 formulate할 수 있다.

$\phi^{GMF}=p_u^G\odot q_i^G$
$\phi^{MLP} = a_L(W_L^T(a_{L-1}(..a_2(W_2^T[[p_u^M],[q_i^M]]+b_2)..))+b_L)$
$\hat y_{ui}=\sigma(h^T[[\phi^GMF],[\phi^{MLP}]])$ $p^G_u$ ,$p^M_u$: user embedding for GMF and MLP
$q^G_i$ ,$q^M_i$: item embedding for GMF and MLP MLP의 activation function : ReLU

이 모델을 NeuMF(Neural Matrix Factorization)이라고도 한다.

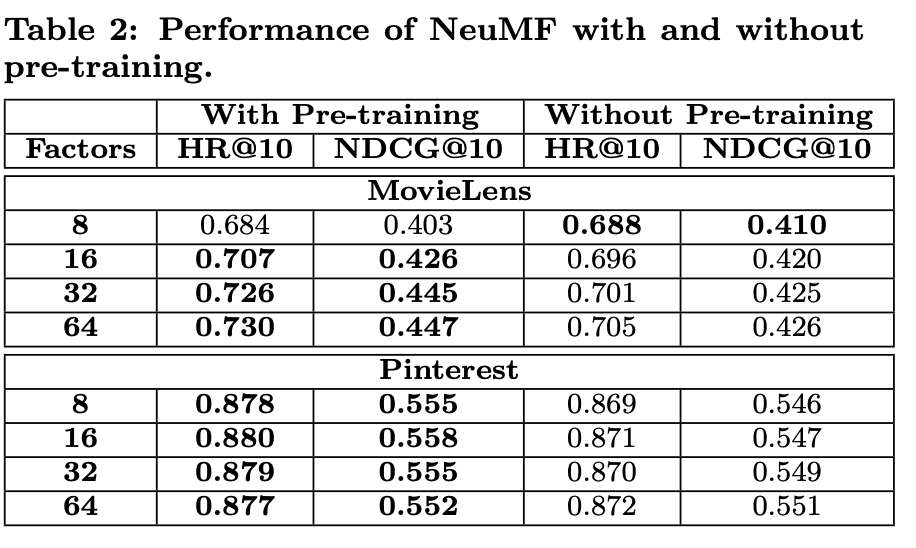
3.4.1 Pre-training

NeuMF의 objective function이 non-convexity하기 때문에, gradient-based optimazation 방법에서는 local optima밖이 찾아내지 못한다. deep learning model의 성능과 convergence에 대한 중요한 role에 대해 initialization이 중요한 역할을 한다. NeuMF가 GMF,MLP의 ensemble이기 때문에, pretrained GMF, MLP를 사용하여 NeuMF를 초기화하는 방법을 제안한다. GMF와 MLP 각각에 대해 random initialization을 사용하여 수렴할때까지 학습을 시킨다. NeuMF의 parameter의 일부분으로, 그 모델들의 parameter를 초기화 값으로 사용한다. 두게의 모델의 weight를 concatenate하는 output layer에서만 다음 식을 적용한다.

$h←[[\alpha h^{GMF}],(1-\alpha)h^{MLP}]$
$h^{GMF},h^{MLP}:$ h vector of the pretrained GMF, MLP model을 의미한다.
$\alpha$ : 두개의 pretrained model간에 trade-off를 결정하는 hyper-parameter를 의미한다.

GMF, MLP 모델을 학습시킬때 Adam optimizer가 SGD보 NeuMF에 pretrained parameter를 feed한 후에, Adam이 아닌 SGD를 사용하였다. Adam은 parameter를 적절히 업데이트하기 위해선 momentum Info를 저장해야했기 때문이다.

4. Experiments

다음 세가지 질문에 대해 대답하는 것을 목적으로 실험을 했다.

Do our proposed NCF methods outperform the state- of-the-art implicit collaborative filtering methods?
How does our proposed optimization framework (log loss with negative sampling) work for the recommendation task?
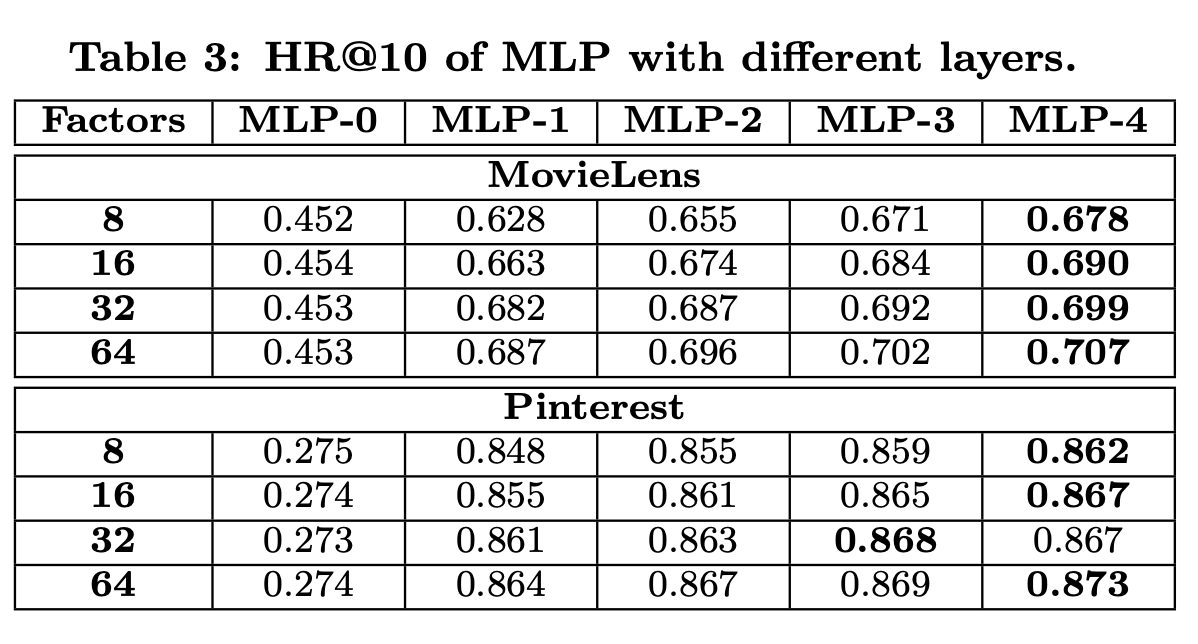
Are deeper layers of hidden units helpful for learning from user–item interaction data?

4.1 Experimental Settings

MovieLens and Pinterest, 2가지 데이터셋을 사용한다.

MovieLens : (MF에서 내가 사용한 데이셋이다.) CF 알고리즘에서 널리 사용되는 데이터셋이다. 각 유저는 최소한 20개의 rating을 한 데이터이다. explicit data이기 떄문에, 의도적으로 rated되었으면 1, 안했으면 0으로 transform하여 data를 implicit data로 바꿨다.
Pinterest : implicit feedback은 content based image recommendation을 위해 construct되었다. original data는 매우 sparse하다. (20%가 넘는 user는 하나의 핀만 갖고있고, cf로 평가하기 어렵다) Movielens와 유사하게 20개이상의 핀만 갖고있는 image를 interaction으로 보았다. 총 데이터는 55187명의 user, 1500809개의 interaction을 포함한다.

Evaluation Protocols

item 추천에 대해 널리 사용되는 leave-one-out evaluation을 사용했다. 각 유저에 대해 가장 최신의 interaction을 testset으로 하고, 나머지 데이터를 학습에 사용한다. evaluation동안 모든 유저에 대해 모든 아이템을 rank하는 데에는 너무 많은 시간을 사용하기 때문에, common strategy인 다음 전략을 사용한다. user에 의해 interact되지 않은 100개의 sample item에서 test item에 대한 rank를 계산한다. Hit Ratio(HR), Normalized Discounted Cumulative Gain(NDCG)를 이용해 ranked list를 평가한다. HR은 top-10 list에 test item이 있는지 평가하고, top rank에 대해 더 높은 점수를 할당하는것으로 position of hit을 평가한다. 각 test user에 대해 두개의 metric모두 평가하고, average score를 산출한다.

Baseline

baseline으로는 다음과 같은 것들과 비교했다.

ItemPop : Items are ranked by their popularity judged by the number of interactions
ItemKNN : This is the standard item-based collaborative filtering method.
BRP : This method optimizes the MF model of Equation 2 with a pairwise ranking loss, which is tailored to learn from implicit feedback.
eALS : This is a state-of-the-art MF method for item recommendation. It optimizes the squared loss of Equa- tion 5, treating all unobserved interactions as negative in- stances and weighting them non-uniformly by the item popularity.

Parameters Settings

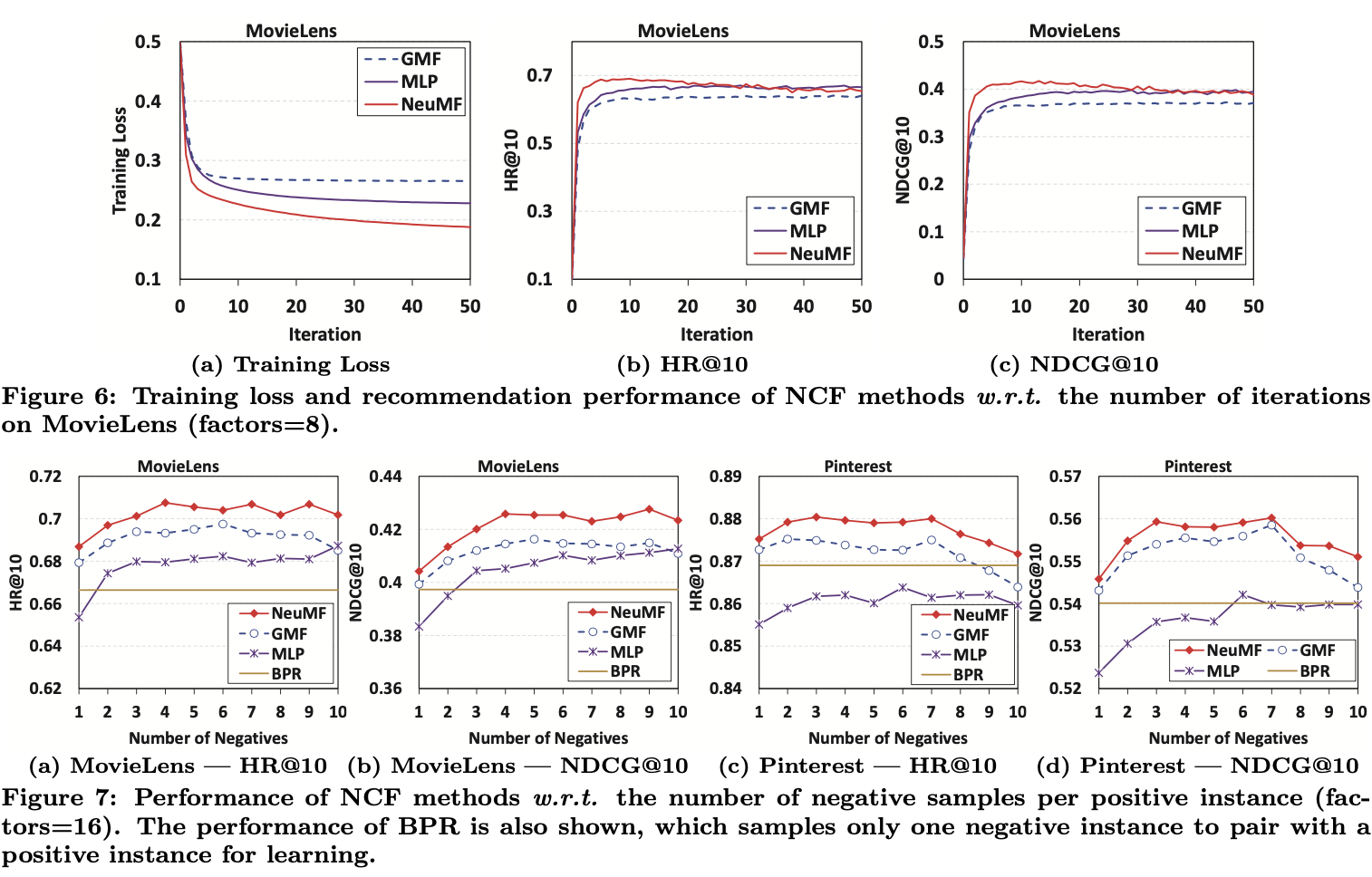
hyper parameter를 결정하기 위해 validation set은 randomly sample하여 사용했고, validation set에 대해 hyperparameter를 이용하여 tune했다. 모든 NCF 모델은 log loss를 optimize하는 것을 학습되고,하나의 positive instance당 4개의 negative instance가 있게 sample했다. model parameter들은 Gaussian distribution (with a mean of 0 and standard deviation of 0.01)으로 random하게 초기화 되고, mini-batch Adam으로 optimize된다. 실험한 하이퍼 파라미터는 다음과 같다.

batch size of [128, 256, 512, 1024],
learning rate of [0.0001 ,0.0005, 0.001, 0.005]
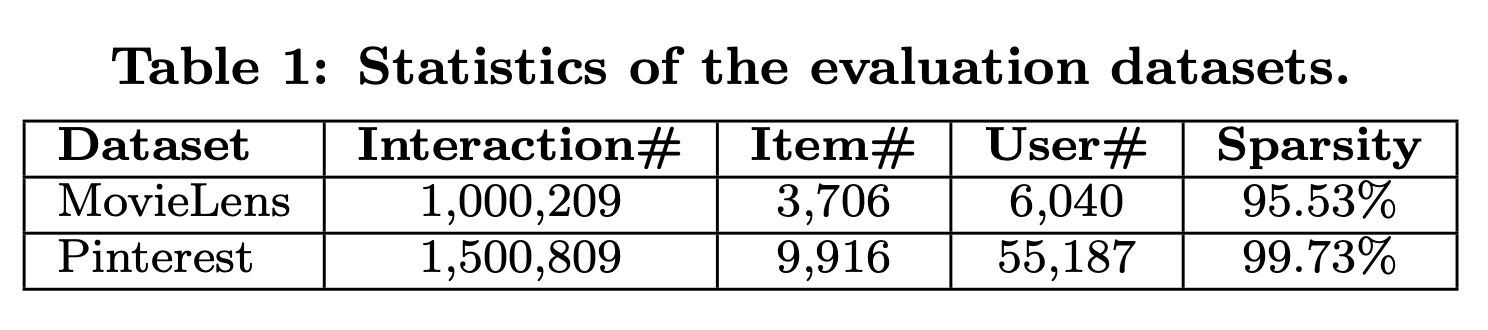
NCF의 hidden layer이 model capacity를 정하기 때문에, hidden layer의 factor를 predictive factors라고 칭했고, [8, 16, 32, 64]에 대해 평가했다.
MLP의 각 layer의 factor 개수들은 predictive factor값에 맞춰서 정했다. 예를들어 3개의 layer라면, 32 -> 16 -> 8개로 정했다. 이떄 user-embedding, item-embedding은 16개씩되어야, 첫번째 layer의 dimension과 일치한다.
NeuMF with pre-training, α was set to 0.5

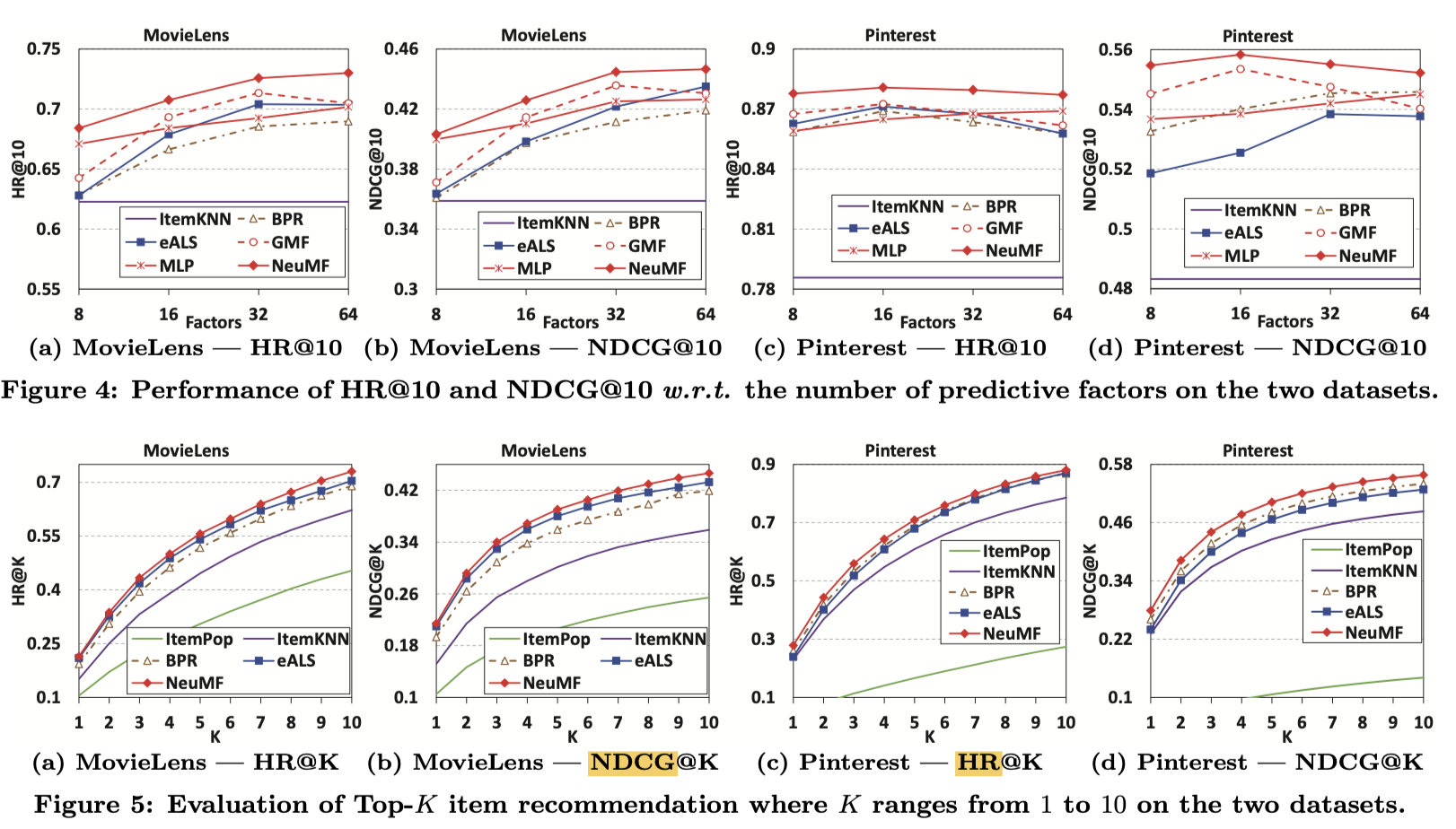
4.2 Performance Comparision (RQ1)

위에서 목표한 첫번째 질문에 대한 답이다.

결론만 말하자면, NeuMF가 다른 모든 Baseline들보다 성능이 좋았다.

그리고 MLP, GMP만 사용하는것보다 같이 사용하는 NeuMF가 더 좋다는 것을 확인할 수 있었다.

4.3 Log Loss with Negative Sampling (RQ2)

4.4 Is Deep Learning Helpful? (RQ3)

ChangHyeon Nam's Blog notes and thoughts