Matrix Factorization Techniques for Recommender Systems

21 Dec 2021

2009년에 발표된 Matrix Factorization Techniques for Recommender Systems 논문을 review 내용입니다.

Matrix Factorization 논문에서 제가 생각한 핵심과 제가 구현한 모델의 간단한 설명은 다음과 같습니다.

기존의 content filtering approach 얻기 쉽지 않은 content info가 필요한 경우도 있고, user-item에 대한 dataset을 characterize하기 위한 profile을 추가로 생성해야 했다.
collaborative filtering는 크게 2가지 (1) Neighborhood method 와 (2) latent factor model이 있고, 전자는 메모리,시간복잡도,성능 면에서 후자보다 좋지 못하다. Latent factor model 중 가장 성공적인 방법이 MF라고 한다.
MF는 user-item interaction에 대해 latent factor들을 inner product(dot product)하여 target에 대한 Matrix를 완성시킨다. Implicit feedback, explicit feedback을 모두 고려하여 MF를 구현할 수 있다.
기존의 SGD(stochastic gradient descent)방식으로 optimize하게 되면 다음과 같은 단점이 존재한다. 첫번째로 user factor와 item factor를 독립적으로 update 시키기 때문에, 단순히 parallelization하는 알고리즘(모델)이 될 수 있다. 두번째로, 실제 dataset 혹은 implicit feedback들은 sparse한 dataset들에 대한 성능이 좋지 않을 수 있다. 이 논문에서 두가지에 대해 SGD보다 성능이 더 좋은 ALS(Alternating Least Squares)방(stochastic gradient descent)을 제안한다. ALS는 간단하게 설명하면, user와 item 각각의 unknown factor들을 동시에 update하는데에 사용하는 cost function은 convex하지 않기 때문에 한쪽을 fix하고 학습시키고, 다시 다른한쪽을 fix하고 학습시키는 시키는 방식으로 quadratic하게 optimize하게된다.
이때, (1) bias, (2) cold start problem을 다루는 방법, (3) temporal Dynamics (4) confidence score를 prediction에 관한 항을 추가하여 구현한다.
제가 구현한 모델은 bias, confidence score만을 추가하여 구현하였습니다. 제가 추가한 bias항은 다음과 같습니다. bias of user[i]: i번째 user의 평균 rating, bias of item[i]: i번째 item의 평균 rating, $\mu$: 전체 평균 rating을 의미합니다.
confidence score에 대한 구체적인 식의 설명이 없어서, 논문에서 말한 정의를 바탕으로 제가 정해서 사용했습니다. MovieLens data를 기반으로 모델을 구현하였는데, 해당 dataset은 user-based dataset이므로, user-based confidence score를 구현했습니다. user-based confidence score[i]는 i번째 user가 rating한 횟수를 의미합니다. 이 confidence score를 normalization를 적용시켜 사용했습니다.

해당 모델의 구현은 Matrix Factorization with MovieLens를 참고해주세요.

Abstract

Netflix Prize competition에서 matrix factorization model이 고전적인 nearest-neighbor technique보다 더 좋은 성능을 보인다고 증명했다. Matrix Factorization에서는 implicit feedback, temporal effect, confidence level과 같은 additional한 정보를 incorporate한다.

Recommender System Strategies

Recommender system은 기본적으로 두가지 전략에 기저한다.

content filtering approach
collaborative filtering

Content filtering

Content filtering 접근에서는 각 유저 또는 제품에 대해 raw한 데이터를 characterize하기 위한 profile을 생성해야한다.
예를들어, movie profile은 장르, 참여한 배우, box office에서의 인기 등을 포함한다. 그리고 user profile은 인구 통계학적 정보, suitable한 질의에 대한 답변 등을 포함한다.
당연하게도, content-based 전략은 collect하기 쉽지 않거나, 불가능한 external 정보를 요구한 경우가 있다.

Collaborative filtering

Collaborative filtering은 past user behavior에 의존한다. 예를들어 previous transaction 또는 product rating에 관한 것이고, 이것들은 explicit profile(content filtering에서 요구하는 content profile, user profile)을 생성하는 것을 요구하지 않는다.
Collaborative filtering은 유저 간의 relationship과 새로운 user-item association을 식별하기 위한 product에서의 interdependency를 분석한다.
CF의 주요한 장점은 domain-free하다는 것이고, 파악하기 어렵거나 profile(content filtering을 사용하기 위해) 하기 어려운 data도 다룰 수 있다.
Content filtering보다 보통 더 정확하지만, cold start problem에 대해서는 content filtering이 더 우월하다.

Collaborative filtering의 대표적인 두가지 area는 (1) neighborhood methods (2) Latent factor models 이다.

Neighborhood methods

Neighborhood methods는 item들 간의 또는 유저 간의 관계를 계산하는 데에 집중한다.

Item-oriented approach는 같은 유저에 의해 neighboring되는 아이템들의 rating에 기저하여 user’s preference를 예측한다.

product의 neighbor들은 비슷한 rating을 갖는 product들이다. (같은 유저에 rated 되는) 예를들어, 영화 데이터 셋에서 어떤 영화에 대해 추천을 할때, 해당 유저에 의해 rate 되는 영화 들중, 비슷하게 rating되는 해당 영화의 nearest neighbor들을 추천하게 된다.
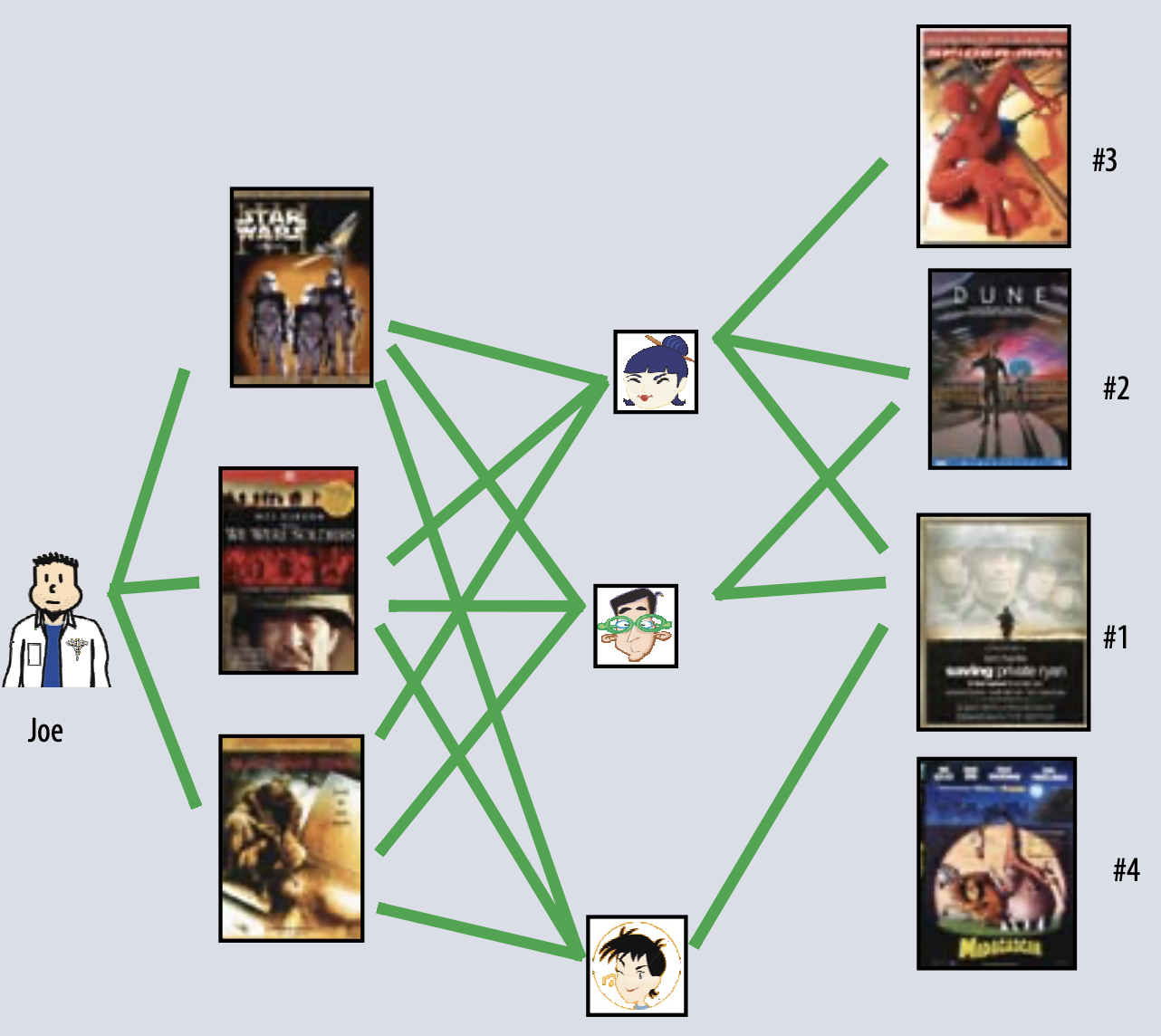
다음 아래 그림은 user-oriented approach에 대한 내용이다.

Joe가 좋아하는 영화들을 좋아하는 비슷한 user를 기저하여 영화를 추천하게 된다. 위의 경우 세명의 유저 모두 라이언 일병 구하기를 좋아하므로, 첫번째 추천으로 라이언 일병 구하기를 추천하게 된다. 2번째 추천 영화로는 2명이 좋아하는 영화 중 하나를 추천하면 된다.

Latent factor models

예를들어, item과 user를 characterize하는 20~100개의 factor가 있고, 이 factor들이 rating pattern infer(설명)할 수 있다고 할때, 이 factor들을 이용하여 rating을 설명하려는 모델이다.

예를들어 factor들은 다음과 같다. comedy versus drama, amount of action, or orientation to children 과 같은 obvious dimension을 갖는 factor들일 수 있고, character development or quirkiness; or completely uninterpretable dimensions를 갖는 less well defined factor들일 수있다.
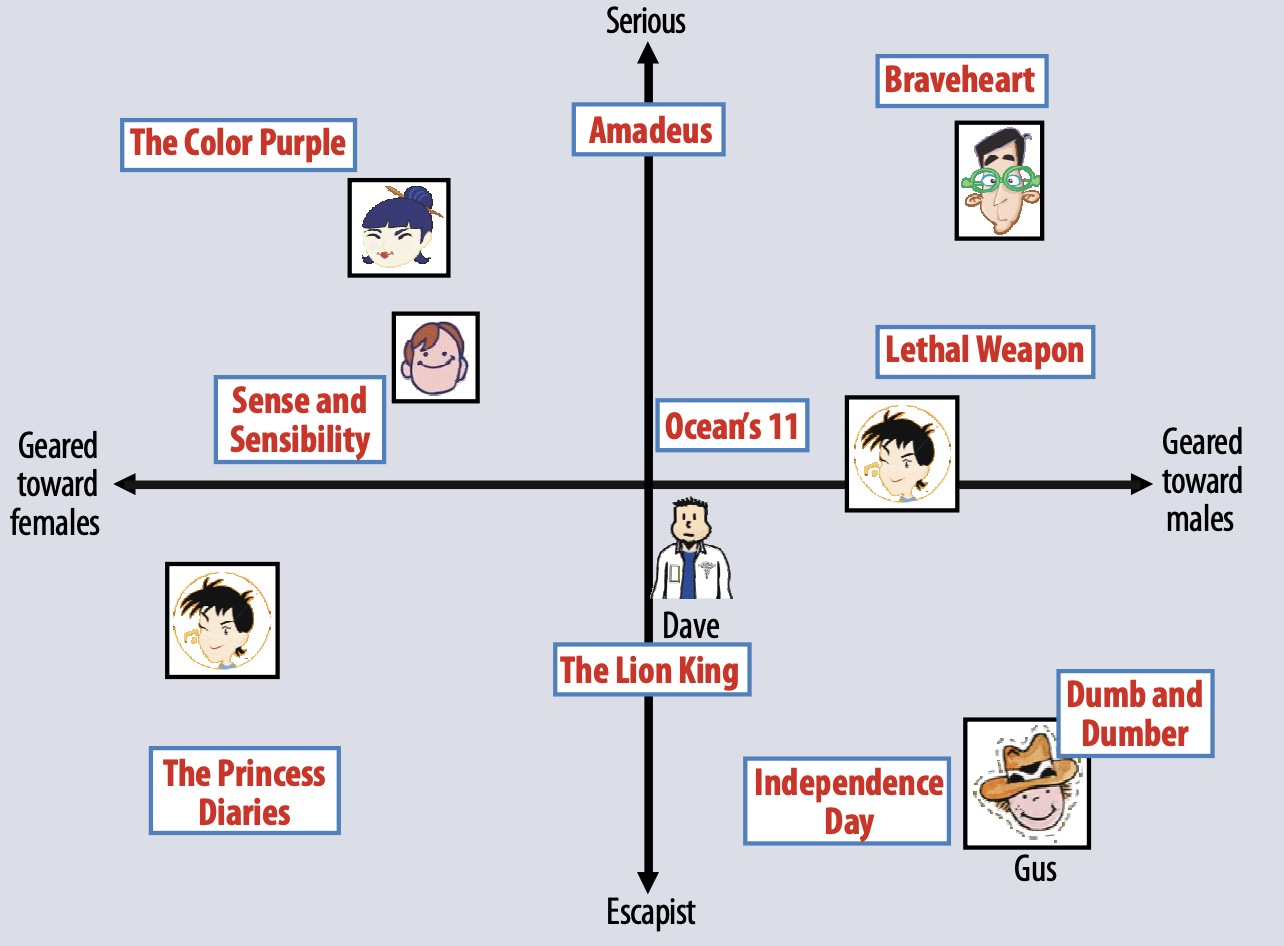
아래 그림은 두가지 dimension에 대해 설명한것이다.

two hypothetical dimensions characterized as (1) female- versus male-oriented and (2) serious versus escapist.

영화의 평균 rating에 대한 user’s predicted rating은 위의 graph상의 movie와 user의 위치의 dot-product이다.

Matrix Factorization Methods

Matrix factorization을 기저한 model이 latent factor model의 가장 성공적인 구현이다. Matrix factorization은 item rating pattern으로 부터 infer된 factor의 vector에 의해 item, user 모두를 characterize 한다.
Item과 user factor사이의 높은 correspondence갖는 것을 추천하게 된다. 이 방법은 predictive accuracy와 좋은 scalability를 결합하여 인기를 얻게 되었다. 추가적으로 다양한 상황에 대한 flexibility를 제공한다.
추천시스템은 다른 타입의 input data에 의존하게 되는데, matrix로써, user를 represent 하는 하나의 dimension과 item에 대한 interest를 represent하는 다른 dimension으로 이뤄진다.
Data type을 크게 두가지로 나눌 수 있다. (1) Explicit feedback (2) implicit feedback

Explicit feedback & Implicit feedback

가장 편리한 데이터로, user의 product interest에 관한 explicit input을 포함한다. Netflix에서 영화에 매기는 star가 그 예이다. 이러한 데이터를 explicit user feedback이라 부른다.
explicit feedback은 보통 sparse matrix로 이뤄집니다. sparse matrix는 item들에 대해 매우 적은 퍼센티지로 rate된 matrix를 의미합니다.
MF의 장점 중 하나는 additional info를 incorporate할 수 있다는 것이다. explicit feedback이 불가능한 경우 implicit feedback을 사용하면 된다.
Implicit feedback은 purchase history, browsing history, search patterns, mouse movements와 같은 user behavior를 관찰하는 data를 의미한다.
Implicit feedback은 보통 이벤트의 presence or absence로 나타내지기 때문에 densely filled matrix로 represent된다.

A Basic Matrix Factorization Model

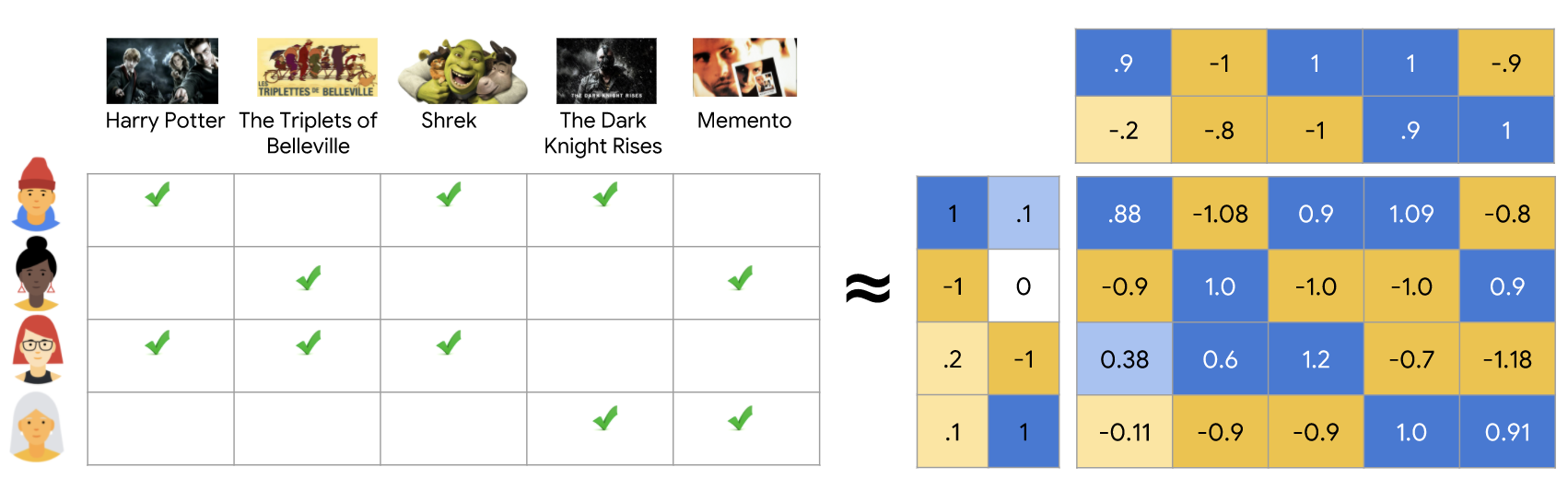Untitled (from developers.google.com)

Matrix Factorization Model은 user와 item 모두를 mapping하여 latent factor space of dimensionality f로 합친다. user-item interaction은 latent factor space에서 inner product로써 표현된다.
$q_i$: vector of each item i. 주어진 item i에 대해 각 item이 어떠한 factor들을 소유하는 정도에 따라 양수 혹은 음수의 값을 갖는다.
$p_u$: vector of each user u. 유저가 item와 관련된 factor들의 interest 정도에 따라 양수 혹은 음수의 값을 갖는다.
$\hat r_{ui} = q^T_ip_u$: 위 vector의 결과인 dot product로써, user u와 item i간의 interaction을 capture한다. (item의 characteristic에 관한 전반적인 유적의 interest를 의미) 이것은 item i에 대한 user u의 rating을 approximate하고, $r_{ui}$로 표현한다.
가장 challenge한 것은 각 item과 user를 factor vector로 mapping하는 것이다. mapping한 후에는 위의 dot product를 통해 쉽게 rating을 estimate할 수 있다.
information retrieval 분야에서 latent semantic factor를 identify할 때 well established technique인 SVD (singular value decomposition)과 매우 밀접하게 연관되어 있다.

Collaborative filtering domain에 SVD를 적용하는 것은 user-item rating matrix를 factoring하는 것을 요구한다. user-item rating matrix에서의 sparseness로 인한 high portion of missing value 때문에 적용하기 어려울 수도 있다.

Conventional한 SVD는 matrix가 불완전할때, undefined되어 있다. 더욱이, 상대적으로 적은 known entry로만 다룬다면 쉽게 overfitting될 수 있다.

초기 시스템은 imputation(결측값 대체)에 의존하여 missing rating을 채웠고, rating matrix를 dense하게 만들었습니다. 하지만 imputation은여러 방면에서 expensive하고, 부정확한 imputation은 데이터를 왜곡할수 있다.
그래서 recent work에선 observed rating만을 사용하여 모델링 하는것을 제안한다. 또한 regularize된 model를 사용하여 overfitting을 피한다.

$\min\limits_{q,p} \sum\limits_{(u,i)\in k}(r_{ui}-q^T_ip_u)^2+\lambda(\mid\mid q_i \mid\mid ^2+ \mid\mid p_u\mid\mid^2)$

k는 training set에서의 (u,i) pair를 의미한다. $r_{ui}$는 관측치, $q_i^Tp_u$는 측정치를 의미한다. regularized squared error를 최소화하고, $\lambda$ 값에 따라 regularization 정도를 결정한다.

Learning Algorithms

MF에서 costfunction을 minimize하는 두가지 접근 방법이 stochastic gradient descent (SGD)와 alternating least squares(ALS)가 있습니다. SGD의 설명에 대해선 생략하겠습니다.

Alternating Least Squares

$q_i,p_u$가 unknown값이기 때문에 (MF에서 예측하려는 vector들), cost function이 convex하지 않다. ALS에서는 unknown중 하나를 fix하여, optimazation problem이 quadratic하게 만든다. ALS는 $q_i$를 고정하는것과 $p_u$를 고정하는 것을 rotate한다. $p_u$를 모두 고정하면, 시스템은 least-squares problem를 해결함으로써, $q_i$를 recompute하고, 반대로도 한다. 이 rotate를 costfunction이 수렴할때 까지 반복한다.

general한 SGD방식이 ALS보다 쉽고 빠르지만, 두가지 케이스에서 ALS이 더 좋다.

시스템은 parallelization을 사용하는 케이스이다. 시스템은 각 $q_i$를 다른 item factor들에 대해 독립적으로 계산하고, $p_u$또한 다른 user factor에 대해 독립적으로 계산한다. 이러한 경우 매우 거대한 parallelization of the algorithm이 될 가능성이 있다.
두번째 경우는 시스템이 implict data에 초점을 맞춘 경우이다. sparase한 training set에 대해 반복해서 SGD를 돌리면 practical 하지 못하고, ALS가 이러한 문제점을 해결할 수 있다.

Adding Biases

MF로 CF를 접근하는 방법의 장점 중 하나는 다양한 데이터와 다른 application의 특정한 요구사항에 대해 flexibility가 있다는 것이다.

$\hat r_{ui} = q^T_ip_u$ 은 user들과 item사이의 interaction을 capture하여 rating value를 생성한다. 하지만 어떠한 interaction과도 독립적인 biases(user 혹은 item에 연관된 effect )때문에 rating value에 대해 많은 variation이 관찰된다.

예를들어 전형적인 CF에서는 어떠한 유저들이 다른 유저들보다 더 높게 rating을 주거나 어떠한 item들이 다른 것들보다 더 높게 rating을 받는 large systematic tendency를 보인다. 결론적으로, 그 product들은 다른것보다 낫다고 인지된다. 그러므로 $q_i^Tp_u$만으로 full rating value를 설명하는 것은 옳지 않다.

대신에 시스템은 이 값들에 대해 bias를 이용하여 identify한다. 이러한 것을 각각의 user or item들의 bias가 설명할 수 있고, true interaction만을 이용하여 model을 구성한다. 그 식은 다음과 같다.

$b_{ui} = \mu+b_i+b_u$

각 bias항은 user effect, item effect에 관한것이다. overall average rating은 $\mu$로 나타낸다.

예를들어 Joe라는 사람의 타이타닉 영화에 대한 estimate rating을 계산한다고 해보자. 전체 영화들에 대한 타이타닉의 평균 overall average $\mu$ = 3.7. Titanic이라는 item은 평균보다 0.5 더 높은 rating을 갖는다, $b_i=0.5$. Joe는 평균보다 0.3정도 낮게 rating을 하는 경향이 있다, $b_u=-0.3$. 결론적으로, Joe에 의한 타이타닉 rating은 3.7+0.5-0.3 = 3.9이다.

앞에서 말한 cost function에 bias 항을 추가하여 optimize하면 된다.

$\min\limits_{q,p} \sum\limits_{(u,i)\in k}(r_{ui}-\mu-b_i-b_u-q^T_ip_u)^2+\lambda(\mid\mid q_i \mid\mid ^2+ \mid\mid p_u\mid\mid^2+b_u^2+b_i^2)$

Additional input sources

추천시스템은 cold start problem을 반드시 다뤄야 하는 경우가 많다. cold start problem이란 많은 유저가 적은 rating을 제공하여, 그들의 선호도를 결정하기 어려운 경우를 의미한다.

이 문제를 완화하는 방법은 user에 대한 implicit feedback을 사용하는 것이다. 또한 추천시스템은 user preference에 대한 insight를 얻기위해 implicit feedback을 사용할 수 있다.

Boolean implicit feedback을 간단한 예로 들어보겠습니다. $N(u)$는 user u가 implicit preference를 나타내는 set of item을 의미한다고 해보자. $N(u)$안에 있는 item들에 대해 preference를 보이는 user는 다음과 같이 벡터로 characterize될 수 있다.

$\sum\limits_{(i\in N(u)}x_i$

그리고 다음과 같이 합을 Normalization하는 것이 더 beneficial 하다.

$\mid N(u)\mid ^{-0.5} \sum\limits_{(i\in N(u)}x_i$

또 다른 정보로 user attribute라고 알려진, demographics를 사용할 수 있다. Boolean attribute로, user u와 연관된 set of attribute를 $A(u)$라 하자.각 attribute에 연관된 user에 대한 vector를 다음과 같은 식으로 표현할 수 있다.

$\sum\limits_{(a\in A(u)}y_a$

matrix factorization model은 enhanced user representation과 함께 모든 signal source를 incorporate할 수 있다.

$\hat r_{ui}=\mu+b_i+b_u+q^T_i[p_u+\mid N(u)\mid ^{-0.5} \sum\limits_{(i\in N(u)}x+\sum\limits_{(a\in A(u)}y_a]$

Temporal Dynamics

이전의 모델은 static했다. Reality에서는 product perception과 popularity가 계속해서 변하고, 새로운 selection이 생긴다. 이와 유사하게 customer의 경향또한 evolve하며, 그들의 선호도를 재정의 하게 된다. 그러므로 system은 user-item의 dynamic, time-drifting 속성을 반영하는 temporal effect를 고려해야한다.

세가지 temporal effect를 고려하여 각 항을 time of function으로 만들면 다음과 같다. Item biases $b_i(t)$, user biases $b_u(t)$, and user preferences $p_u(t)$. 또한 rating at time t를 다음과 같이 나타낼 수 있다.

$\hat r_{ui}=\mu+b_i(t)+b_u(t)+q^T_ip_u(t)$ .

Inputs with varying confidence levels

모든 observed rating들이 같은 weight 또는 confidence로 고려되어선 안된다. 예를들어 massive advertising에서는 특정 item에 대한 long-term characteristic을 반영하지 못한다. 유사하게, 시스템은 특정 item들에 대해 일부러 rating을 바꾸려는 adversarial user를 만날수도 있다.

다른 예시는 implicit feedback으로 시스템을 빌드 할 경우이다. Ongoing user behavior를 해석하려는 시스템의 경우, user’s exact preference는 정량화하기 어렵다. 그래서 이러한 시스템은 “아마 이 제품을 좋아할 것이다.” 또는 “좋아하지 않을것이다” 와 같은 cruder binary representation으로 동작하게 된다.

이러한 케이스에서, estimated preference에 confidence score를 추가하는 것은 의미가 있다. Confidence는 action의 빈도를 묘사하는 numerical value이다, 예를들어 user가 특정 show를 얼마나 보았는지 또는 user가 특정 item을 몇번 구매했는지에 관한 값이다. 반복되는 event는 user의 의견을 반영할 가능성이 높다.

$\min\limits_{q,p} \sum\limits_{(u,i)\in k}c_{ui}(r_{ui}-\mu-b_i-b_u-q^T_ip_u)^2+\lambda(\mid\mid q_i \mid\mid ^2+ \mid\mid p_u\mid\mid^2+b_u^2+b_i^2)$

$c_{ui}$항을 이용하여 confidence level에 따라서 weight를 조절할 수 있다.

Netflix Prize competition

이 논문을 쓴 BellKor team의 competition solution에 관한 구체적인 내용이다.

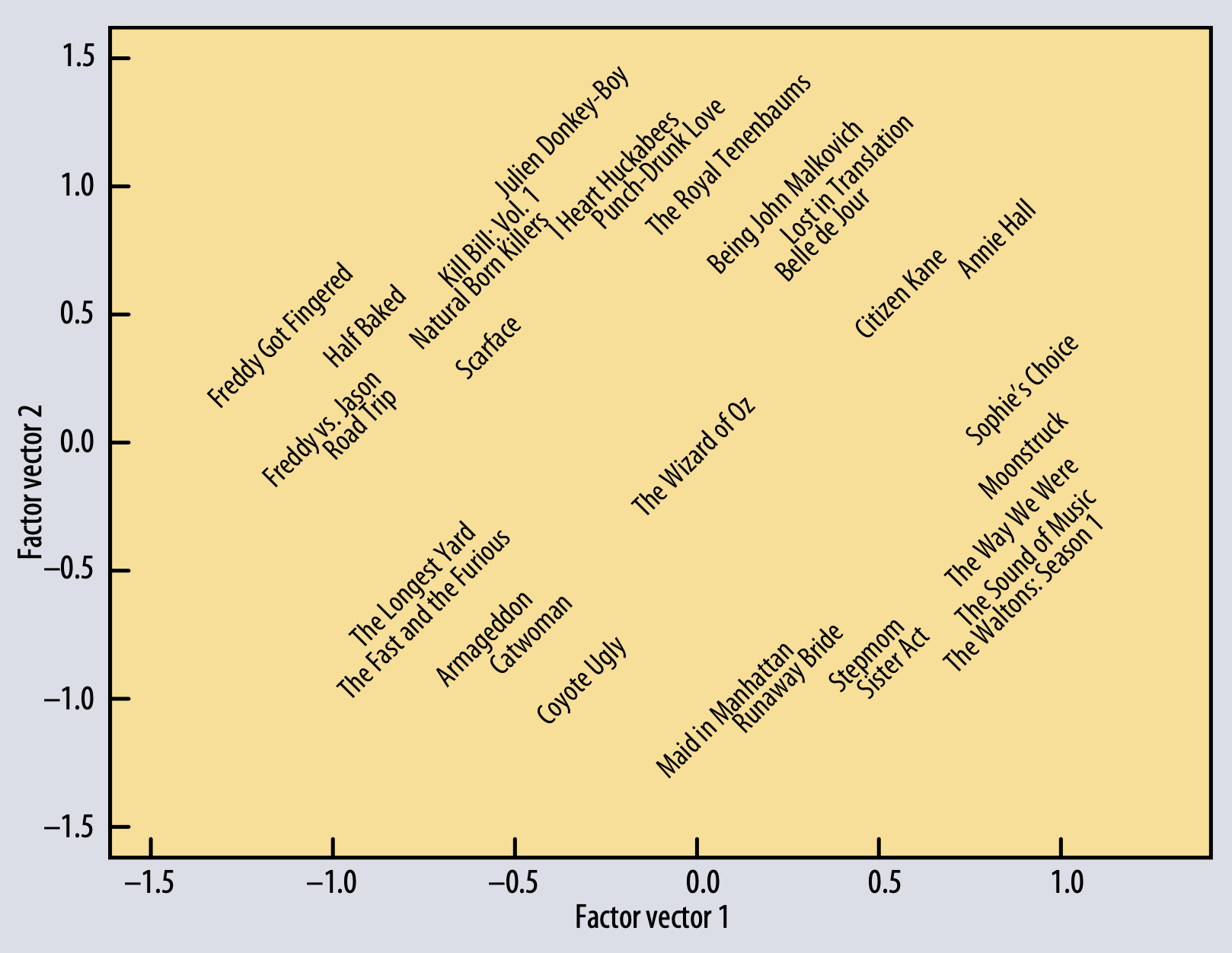
Netflix user-movie matrix를 Factorizing하는 것은 movie preference를 예측하기 위해 가장 descriptive한 dimension을 발견하게 해주었다고 한다. Matrix decomposition을 통해 factor vector중 두가지를 위의 그림에 표현한것이다. distinct genre을 포함하여 strong female leads, fraternity humor, and quirky independent films의 cluster들을 잘 표현하고 있다.

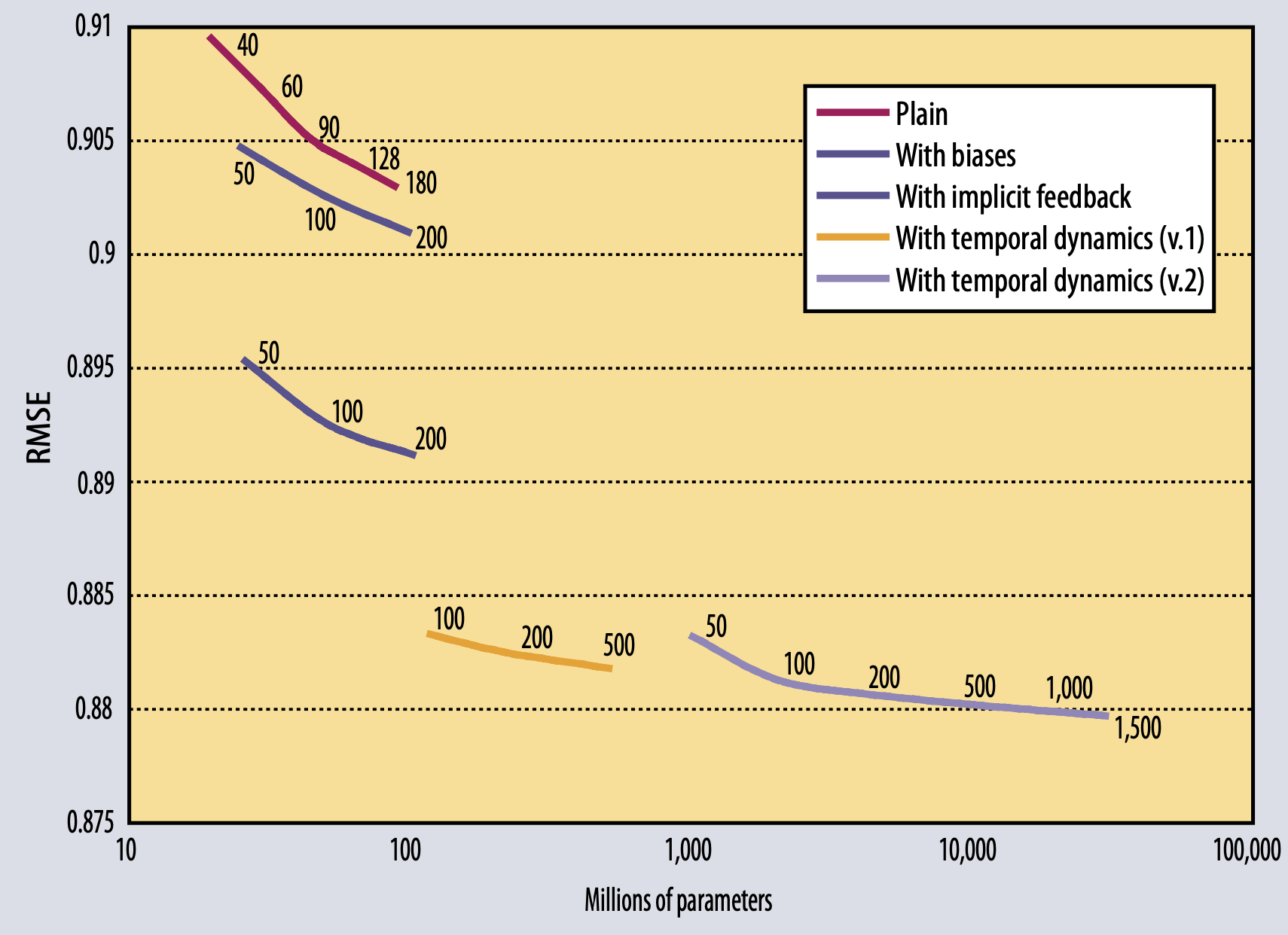
plain factorization, adding biase, enhancing user profile with implicit feedback, two variants adding temporal components에 따른 여러가지 모델의 RSME 지표를 보여주고 있다.

ChangHyeon Nam's Blog notes and thoughts