ChangHyeon Nam's Blog notes and thoughts

세그먼트 트리(Segment Tree) 응용

Comments

C번 문제(나무는 쿼리를 싫어해~)에 대해서는 빠른 시일 내에 오프라인 쿼리와 온라인 쿼리를 공부하고 업데이트 하겠습니다.

세그먼트 트리 포스트에 이어서 세그먼트 트리 응용에 대해 다룰려고 합니다.

  • A번은 구간의 연산이 아닌 구간에서의 최댓값을 저장하는 세그먼트 트리에 대한 내용입니다.

  • B번은 분할정복을 이용하는 머지 소트를 메모리제이션 하는 머지소트 트리에 대한 내용입니다. 세그먼트 트리는 분할 정복에 대해 메모리제이션하는 자료구조라고도 볼 수 있습니다.

  • C번에서는 세그먼트 트리에 저장해야 하는 인덱스 범위가 클때 사용하는 다이나믹 세그먼트 트리에 대한 내용 입니다. 오프라인 쿼리,온라인 쿼리 방법으로 모두 구현이 가능합니다.

  • D번 좌표 압축과 스위핑을 이용한 세그먼트 트리 문제입니다. 주어진 구간에서 연속된 부분합의 최댓값을 분할정복을 통한 세그먼트 트리로 해결하는 (유명한?)금광세그 문제입니다.

A. 수열과 쿼리 24

세그먼트 트리는 단순히 구간에 대한 연산 뿐만 아니라 여러 개의 값,상태를 저장할 수 있습니다.

17408번 수열과 쿼리 24

길이가 N인 수열 A에 대해 i번째 수를 갱신하는 연산과 [l,r]이 주어졌을때 $l ≤ i < j ≤ r$ 의 범위에 대해 $A_i + A_j$ 중 에서 최댓값을 구하는 문제입니다.

수열의 크기 $N(2 ≤ N ≤ 100,000)$ 이고, 각 원소가 $A1, A2, …, AN (1 ≤ Ai ≤ 10^9)$ , 쿼리의 개수 M입니다. $(2 ≤ M ≤ 100,000)$

A번 문제는 구간 내에서 가장 큰 두개의 값을 찾는 것입니다. 세그먼트 트리의 각 노드에 최대값과 두번째 최대값을 둘다 저장하면 됩니다.

  • update

      void update(int i, int l,int r, int p, ll x) {
      if(p<l || p>r)
          return ;
      if (l == r) {
          st[i] = {x,0};
          return;
      }
      int m = l + r >> 1;
      update(i * 2,l,m,p,x);
      update(i * 2 + 1, m + 1, r, p, x);
      st[i] = merge(st[i*2],st[i*2+1]);
  }

    리프 노드일 경우{x,0} 을 넣어주고, 아니라면 merge를 통해서 구간 내의 가장 큰 두 값을 해당 노드에 저장해 줍니다.

  • merge

      pi merge(pi a, pi b){
      pi ret;
      if(a.first<b.first) swap(a,b);
      ret.first = a.first;
      ret.second = max(a.second,b.first);
      return ret;
  }

    a 노드(왼쪽 자식노드)와 b 노드(오른쪽 자식노드)에 해당하는 두개의 구간에서의 최대값과 두번째 최대값을 한개의 노드에 합쳐서 반환하는 함수 입니다.

  • query

      pi query(int i, int l,int r, int s, int e){
      if(e<l|| r<s)
          return {0,0};
      if(s<=l&&r<=e)
          return st[i];
      int m= l+r>>1;
      return merge(query(i*2,l,m,s,e),
                   query(i*2+1,m+1,r,s,e));
  }

    주어진 구간 [s,e]에 대해서, merge 함수를 통해 최대값과 두번째 최대값을 찾는 함수 입니다.

code 
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <cmath>
#define endl '\n'
#define INF 1e9
#define LINF 9223372036854775807
using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int> tup;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
priority_queue<tup,vector<tup>,greater<tup>> edge;

int t;
const int N = 100001;
int n;
pi st[4*N];

pi merge(pi a, pi b){
    pi ret;
    if(a.first<b.first) swap(a,b);
    ret.first = a.first;
    ret.second = max(a.second,b.first);
    return ret;
}
void update(int i, int l,int r, int p, ll x) {
    if(p<l || p>r)
        return ;
    if (l == r) {
        st[i] = {x,0};
        return;
    }
    int m = l + r >> 1;
    update(i * 2,l,m,p,x);
    update(i * 2 + 1, m + 1, r, p, x);
    st[i] = merge(st[i*2],st[i*2+1]);
}

pi query(int i, int l,int r, int s, int e){
    if(e<l|| r<s)
        return {0,0};
    if(s<=l&&r<=e)
        return st[i];
    int m= l+r>>1;
    return merge(query(i*2,l,m,s,e),
                 query(i*2+1,m+1,r,s,e));
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    cin>>n;
    for(int i=1,p1;i<=n;i++){
        cin>>p1;
        update(1,1,n,i,p1);
    }
    int m;
    cin>>m;
    for(int i=0,p1;i<m;i++){
        cin>>p1;
        if(p1==1){
            int k,val;
            cin>>k>>val;
            update(1,1,n,k,val);
        }
        else{
            int l,r;
            cin>>l>>r;
            auto[fi,se]= query(1,1,n,l,r);
            cout<<fi+se<<endl;
        }
    }
}

B. 수열과 쿼리 1

문제에 대한 풀이를 하기전에, 머지 소트 트리에 대해 알아봅시다. 앞서 말했듯이, 세그먼트 트리는 분할 정복에 대해 메모리제이션하는 자료구조라고도 볼 수 있습니다. 그리고 이를 이용해 머지소트 트리를 만들 수 있습니다.

Untitled

주어진 수열이 [4, 3, 7, 1, 2, 1, 2, 5]이라고 하면 다음과 같이 정렬 됩니다. 머지 소트할때 구간 크기가 작은 것 순으로 merge하여 소트하는데, 같은 방식으로 머지소트 트리를 구현합니다. 이때 각 노드는 각 구간에 대해 정렬된 원소의 리스트를 저장합니다.

트리의 시간 복잡도는 머지소트와 동일하게 $O(NlogN)$ 입니다. 각 깊이에 모두 N개의 원소가 저장되어 있기 때문에 공간 복잡도도 또한 $O(NlogN)$ 입니다.

13537번 수열과 쿼리 1

길이가 N인 수열 A가 주어지고, 다음 M개의 쿼리를 수행하는 문제입니다.

→ $i,j,k: A_i, A_{i+1}, …, A_j$ 로 이루어진 부분 수열 중에서 k보다 큰 원소의 개수를 출력합니다. 이때 $(1 ≤ N ≤ 100,000)$ , $(1 ≤ A_i ≤ 109)$ , $(1 ≤ M ≤ 100,000)$ 입니다.

원소에 대한 갱신이 없고, 단순히 k보다 큰 원소의 개수를 세면 됩니다.

Untitled

다음과 같이 주어지는 구간에 대해 봐야하는 노드의 개수는 최대 $O(logN)$ 입니다. $O(logN)$개의 노드에 대해 이분 탐색(upper_bound)을 이용하면 $O(log^2N)$이 걸립니다.

  • build

        vector<int>lvec = st[i*2];
      vector<int>rvec = st[i*2+1];
      int lptr = 0, rptr = 0;
      while(lptr<lvec.size() && rptr<rvec.size()){
          if(lvec[lptr]<=rvec[rptr]){
              st[i].push_back(lvec[lptr++]);
          }
          else st[i].push_back(rvec[rptr++]);
      }
      while(lptr<lvec.size())
          st[i].push_back(lvec[lptr++]);
      while(rptr<rvec.size())
          st[i].push_back(rvec[rptr++]);

    build함수 안의 다음 코드를 통해 분할한 노드들을 merge합니다.

code 
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <cmath>
#define endl '\n'
#define INF 1e9
#define LINF 9223372036854775807
using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int> tup;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
priority_queue<tup,vector<tup>,greater<tup>> edge;

int t;
const int N = 100001;
int n;
int a[N];
vector<int> st[4*N];

void build(int i,int l,int r){
    // 기저 사례
    if(l==r){
        st[i].push_back(a[l]);
        return;
    }
    int m = l+r>>1;
    build(i*2,l,m);
    build(i*2+1,m+1,r);
    vector<int>lvec = st[i*2];
    vector<int>rvec = st[i*2+1];
    int lptr = 0, rptr = 0;
    while(lptr<lvec.size() && rptr<rvec.size()){
        if(lvec[lptr]<=rvec[rptr]){
            st[i].push_back(lvec[lptr++]);
        }
        else st[i].push_back(rvec[rptr++]);
    }
    while(lptr<lvec.size())
        st[i].push_back(lvec[lptr++]);
    while(rptr<rvec.size())
        st[i].push_back(rvec[rptr++]);
}

int query(int i, int l,int r, int s, int e,int k){
    if(e<l|| r<s)
        return 0;
    if(s<=l&&r<=e)
        return st[i].end()- upper_bound(st[i].begin(),st[i].end(),k);
    int m= l+r>>1;
    return query(i*2,l,m,s,e,k)+
                 query(i*2+1,m+1,r,s,e,k);
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    build(1,1,n);
    int m;
    cin>>m;
    for(int i=0,p1,p2,k;i<m;i++){
        cin>>p1>>p2>>k;
        cout<<query(1,1,n,p1,p2,k)<<endl;
    }
}

C. 나무는 쿼리를 싫어해~

문제를 풀기전에 문제에 사용되는 다이나믹 세그먼트 트리에 대해 먼저 알아 봅시다. A번과 같은 구간합 구하기에 사용되는 일반 세그먼트 트리의 공간 복잡도는 O(N)입니다. A번에서는 인덱스 의 범위가 10만 정도로 모든 값을 트리에 저장할 수 있었지만, C번에서는 인덱스의 범위가 10억 이기 때문에 일반 세그먼트 트리를 이용할 수 없습니다.

다이나믹 세그먼트 트리는 세그먼트 트리의 메모리 사용량을 줄여주는 테크닉 입니다.

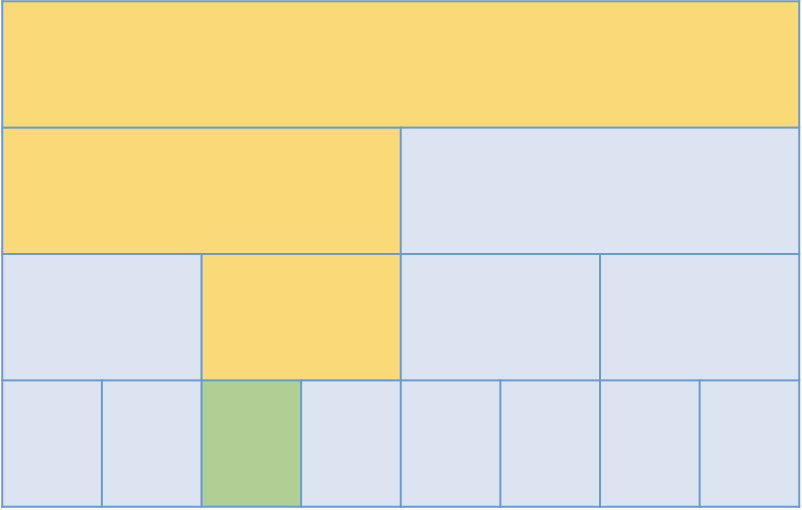
위와 같이 길이 8인 수열이 있다고 해봅시다. 세번째 원소를 갱신하는 경우, 세번째 원소와 관련된 노드들만 갱신하면 됩니다.

그리고 사용하지 않은 노드들은 0으로 초기화 되어있기 때문에, 사용하지 않은 노드들은 필요 없다는 것을 알 수 있습니다.

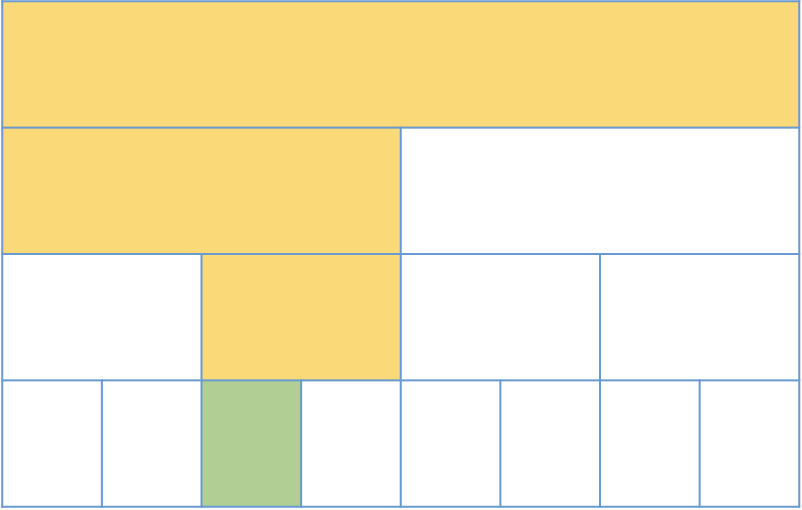
그리고 6번째 원소를 바꾸고 싶다면, 그 노드까지 가는 길에 있는 노드들을 할당해주면 됩니다. 이런식으로 트리의 해당 노드가 필요할때 할당해 주고, 안쓰이는 노드들은 생성을 안하는 방식으로 세그먼트 트리를 만들면 각 쿼리마다 $O(logN$) 개의 노드를 만들게 되고, 공간 복잡도는 $O(min(Q*logN,N))$이 됩니다.

다이나믹 트리의 경우 N이 매우 크기 때문에 공간 복잡도는 $O(Q*logN)$ 라고 봐도 됩니다. (Q는 쿼리의 개수 입니다.)

20212번 나무는 쿼리를 싫어해

수열 A의 길이 N $(2 ≤ N ≤ 50,000)$ 이고, N개의 쿼리가 주어집니다.

1번 쿼리는 주어진 구간에 대해 k를 더하는 것이고, 2번 쿼리는 k번째 1번 쿼리 까지 적용 되었을때 주어진 구간에 대한 합을 구합니다.

$O(Q*logN)$개의 원소를 저장하는 배열을 사용하여 다이나믹 세그먼트 트리를 구현하겠습니다.

(추후 업로드)

D. 금광

10167번 금광

금광들을 지도상에 표시할 때, 평면상의 점들로 표현 됩니다. 각 점 $p_i$에는 양수 또는 음수의 정수값 $w_i$가 주어지고, $w_i$는 음수이면 손해, 양수이면 이익을 의미합니다.

금광 개발업자는 x,y축과 평행한 변을 가진 직사각형 모양의 땅 R을 사서 R에 포함된 금광들을 개발할 것이고, 개발 이익은 R에 포함되는 $w_i$의 합입니다. 개발이익이 최대가 되는 직사각형 영역 R를 찾았을때, 최대 개발 이익을 출력하는 문제입니다.

금광의 개수 $N(1 ≤ N ≤ 3,000)$이고, 각 좌표 $x,y(0 ≤ x, y ≤ 10^9)$이고, 이익 또는 손해를 나타내는 $w_i(-10^9 ≤ w_i≤ 10^9)$. 금광의 좌표는 모두 다르며, w>0인 금광은 적어도 하나 존재합니다.

일단, 좌표의 범위가 $x,y(0 ≤ x, y ≤ 10^9)$이고,주어진 금광의 개수는 3000개 이하이기 때문에 좌표압축을 적용할 수 있습니다. 좌표 압축 시킨 x좌표, y좌표의 범위는 (0,3000)입니다.

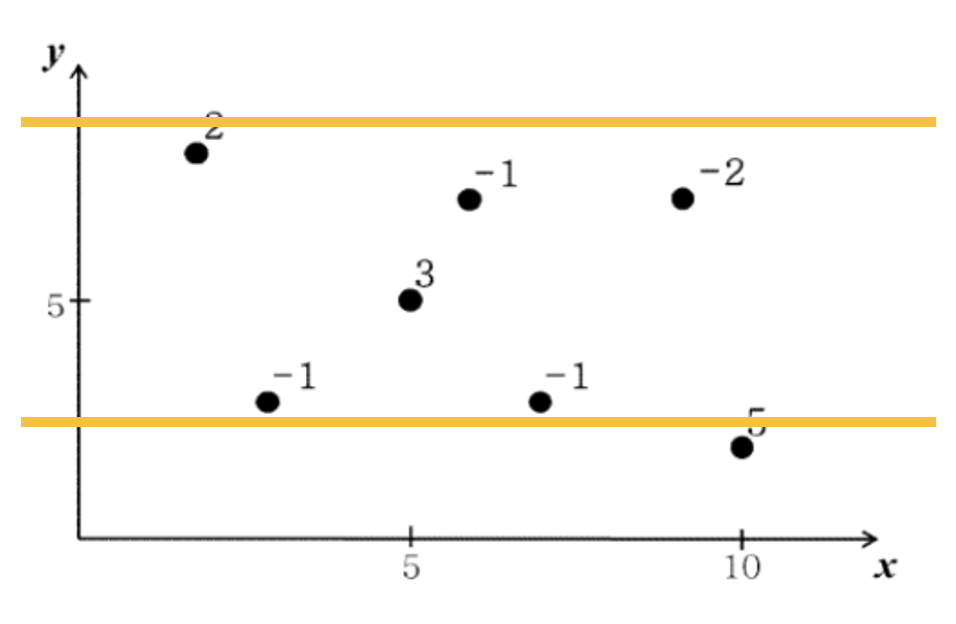
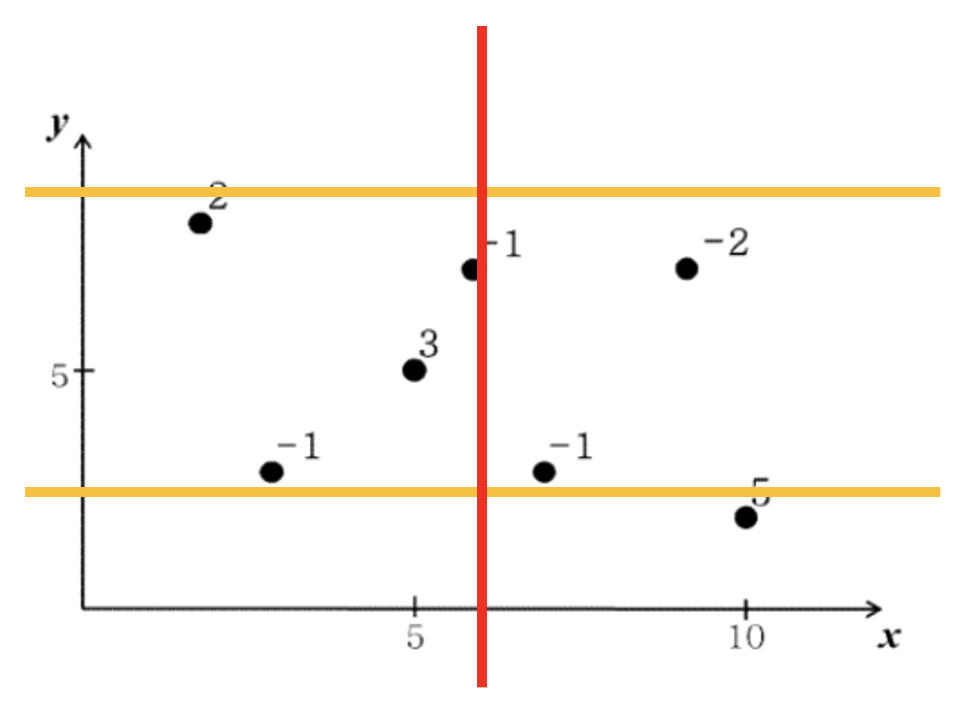
문제를 풀기 앞서 y1,y2가 고정되어 있다고 가정해봅시다.

저 노란 선 사이의 금광만 사용가능하며, 같은 x값을 갖을 경우 반드시 포함되게 됩니다. 모든 (x1,x2)쌍을 고려해 부분합을 계산하는 경우의 수는 O(N^2)이므로 O(N^4)입니다. (앞서 좌표 압축을 통해, y좌표와 x좌표의 범위는[0,n]입니다.) 그러므로 y1,y2가 고정되어 있을때 x1,x2에 대해 다른방법을 고려해봐야 합니다. 똑같은 상황에서 x축에 대해 반으로 나눠 생각해봅시다.

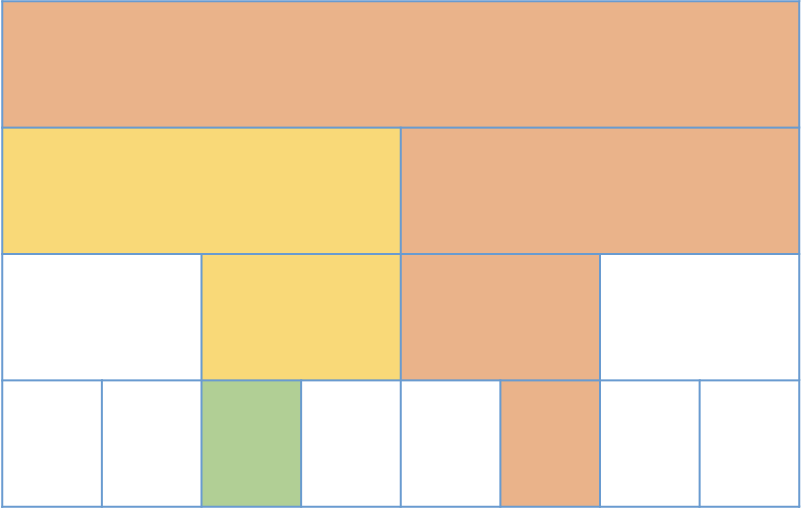
위의 그림에서 문제의 답을 만족하는 (x1,x2) 쌍은 다음 세가지 경우의 수로 존재합니다.

  1. (x1,x2)가 모두 왼쪽에 위치.
  2. x1은 왼쪽, x2오른쪽에 위치.
  3. (x1,x2)가 모두 오른쪽에 위치.

왼쪽 그룹과 오른쪽 그룹으로 분리한 후에, 왼쪽 그룹에서의 모든 (x1,x2)에 대한 구간의 부분합의 최댓값을 구하고, 같은 계산을 오른쪽 그룹에서도 적용해 줍니다. 그리고 나서 (x1,x2)가 다른 그룹에 있을 경우를 merge를 통하여 계산할 수 있습니다. 이런 방법을 분할정복이라고 합니다.

그렇다면 중심(mid)을 지나는 2번째 경우는 어떻게 계산할지 알아봅시다.

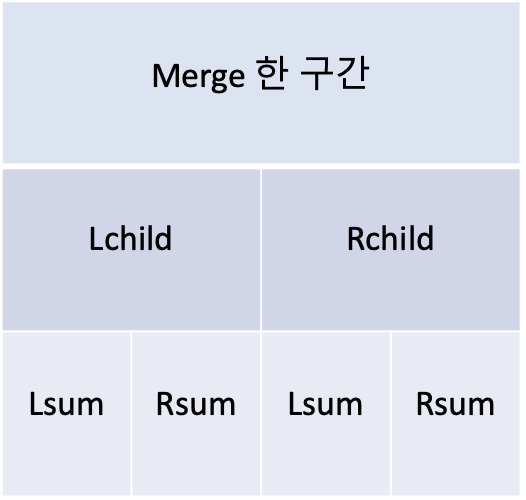
왼쪽구간의 가장 오른쪽 수(mid-1)를 포함하는 가장 큰 부분합(Lsum)과 오른쪽 구간에서 가장 왼쪽 수(mid+1)를 포함하는 부분합(Rsum)의 합이 중심을 지나는 가장 큰 부분합입니다. 다음은 위 설명에 대한 슈드코드입니다.

ret.sum = Lchild.sum + Rchild.sum
ret.Lsum = max(Lchild.Lsum, Lchild.sum + Rchild.Lsum)
ret.Rusm = max(Rchild.Rsum, Rchild.sum + Lchild.Rsum)
ret.max_sum = max(Lchild.max_sum,Rchild.max_sum,
Lchild.Rusm + Rchild.Lsum)

Lsum은 왼쪽 끝값을 포함하는 최대 부분합, Rsum은 오른쪽 끝값을 포함하는 최대 부분합입니다.

이때, 분할정복(O(nlog n)에 (y1,y2)를 고려한 시간 복잡도도 $O(N^3logN)$ 이므로 시간초과가 납니다.

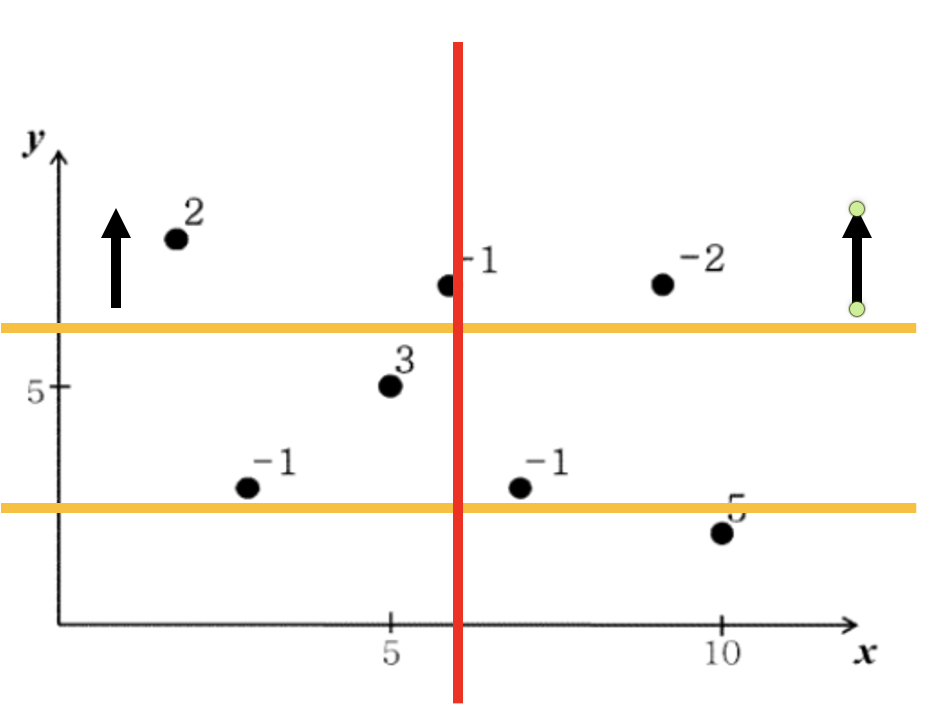
여기서 더 빠른 계산 방법은 y1에서 y2로 값을 증가 시키면서(스위핑) 분할정복으로 계산한 부분합들을 update시키는 방법입니다.

y1을 base로 정해두고 증가되는 y2에 대해 추가되는 금광들에 대한 구간의 부분합들을 update함으로써 시간을 줄일 수 있습니다.

임의의 금광 x 추가될때, 이미 상태값을 갖고있는 구간에 대해서 금광 x가 영향 주는 구간의 개수는 $logN$개입니다. 그 이유는 위에서 설명한 분할정복을 통해 반씩 나눠 계산을 했기 때문입니다.

그러므로 금광이 추가될때 마다 $O(log N)$시간이 걸리므로, $O(N^2logN)$이 걸립니다.

그래서 분할정복을 세그먼트리 트리에 적용한다면 위 방법을 구현할 수 있습니다. 위에서 설명한 분할정복을 위해 노드 구조체를 만들었습니다. 트리의 각 노드는 4개의 정보를 담고 있어야 합니다.

  1. 노드가 담당하는 구간의 왼쪽 끝값을 포함하는 최대 부분합
  2. 노드가 담당하는 구간의 오른쪽 끝값을 포함하는 최대 부분합
  3. 노드가 담당하는 구간의 최대 부분합
  4. 노드가 담당하는 구간의 전체 합

아래의 코드가 위의 설명에 대한 구현입니다.

Node merge(Node a, Node b){
    Node ret;
    ret.lsum = max(a.lsum,a.asum+b.lsum);
    ret.rsum = max(b.rsum,a.rsum+b.asum);
    ret.msum = max(max(a.msum,b.msum),a.rsum+b.lsum);
    ret.asum = a.asum+b.asum;
    return ret;
}

이제 스위핑을 고려해 y2를 y1부터 y_max까지 올리면서 세그먼트 트리를 업데이트하면 풀 수 있습니다.

code 
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <cmath>
#define endl '\n'
#define INF 1e9
#define LINF 9223372036854775807
using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef pair<ll, ll> pl;
typedef tuple<int, int, int> tup;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
priority_queue<tup,vector<tup>,greater<tup>> edge;

int t;
const int N = 10001;
vector<pl>x;
vector<pl>y;
vector<pl>yy[3001];

struct Point {
    int x, y, w;
};
Point p[3001];

struct Node{
    ll lsum;
    ll rsum;
    ll msum;
    ll asum;
};
Node merge(Node a, Node b){
    Node ret;
    ret.lsum = max(a.lsum,a.asum+b.lsum);
    ret.rsum = max(b.rsum,a.rsum+b.asum);
    ret.msum = max(max(a.msum,b.msum),a.rsum+b.lsum);
    ret.asum = a.asum+b.asum;
    return ret;
}
Node st[4*N]; // 적당히

Node update(int i, int l,int r, int p, ll x) {
    if(p<l || p>r)
        return st[i];
    if (l == r) {
        st[i].asum+=x;
        st[i].lsum+=x;
        st[i].rsum+=x;
        st[i].msum+=x;
        return st[i];
    }
    int m = l + r >> 1;
    Node left, right;
    left = update(i * 2,l,m,p,x);
    right = update(i * 2 + 1, m + 1, r, p, x);

    st[i] = merge(left,right);
    return st[i];
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int tx,ty,tw;
        cin>>tx>>ty>>tw;
        x.push_back({tx,i});
        y.push_back({ty,i});
        p[i].w = tw;
    }
    sort(x.begin(),x.end());
    sort(y.begin(),y.end());
    int num = 0;
    for (int i = 0; i < n; i++) //x좌표 압축
    {
        if (i > 0 && x[i - 1].first != x[i].first) num++;
        p[x[i].second].x = num;
    }

    num = 0;
    for (int i = 0; i < n; i++) //y좌표 압축
    {
        if (i > 0 && y[i - 1].first != y[i].first) num++;
        p[y[i].second].y = num;
    }

    for (int i = 0; i < n; i++)
        yy[p[i].y].push_back({ p[i].x, p[i].w });

    ll ans = 0;
    for(int y1=0;y1<n;y1++){
        for(int j=0;j<4*N;j++)
        {
            Node temp;
            temp.asum=0,temp.lsum=0,temp.rsum=0,temp.msum=0;
            st[j]=temp;
        }
        for(int y2=y1;y2<n;y2++){
            for(int i=0;i<yy[y2].size();i++)
            {
                int hx = yy[y2][i].first, hy =y2,hw =yy[y2][i].second;

                update(1,0,N-1,hx,hw);
            }
            ans = max(ans,st[1].msum);
        }
    }
    cout<<ans<<endl;
    return 0;
}

reference

  1. https://anz1217.tistory.com/133
  2. https://blog.naver.com/PostView.nhn?isHttpsRedirect=true&blogId=kks227&logNo=221400656663
  3. https://justicehui.github.io/medium-algorithm/2020/02/28/DynamicSeg/
  4. https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=edenooo&logNo=221415337560
  5. 금광세그 KOI 해설