ChangHyeon Nam's Blog notes and thoughts

세그먼트 트리(Segment Tree)

Comments

세그먼트 트리(segement tree) 는 구간들을 보존하고 있는 트리입니다.

전체 구간이 [0,N-1]인 N개의 공간이 있을때, 각 리프노드 들은 길이가 1인 구간을 갖고 있고, 부모노드는 자신들의 자식들의 구간의 합을 갖고 있으며, 모든 구간이 연속 이어야 합니다. 루트는 전체 구간을 포함하게 됩니다. 이와 같이 구간을 보존하는 트리를 세그먼트 트리라고 합니다.

보통은 완전 이진 트리의 형태를 사용해 전체적으로 동일한 재귀적 구조가 반복되도록 표현하며, 값의 개수가 2^n 꼴이 아닐 때는 남는 구간을 의미없는 포화 이진 트리 형태로 사용합니다. 이렇게 함 으로써, 트리의 높이가 O(logN)가 보장 됩니다.

루트 노드에서 왼쪽 자식, 오른자식 순으로 번호를 매기게 되고, 리프노드들은 n~2n-1번의 번호를 얻게 됩니다.

A. 구간 합 구하기

2042번 구간 합 구하기

구간 합 구하기 문제를 통해 세그먼트 트리의 원리를 설명하겠습니다. 주어진 배열의 원소들이 고정되어 있다면, dp혹은 누적합을 이용하여 구간합을 구할 수 있지만, 배열의 원소가 갱신된다면, $O(N * K)$가 걸려 시간초과가 납니다. 그래서 세그먼트 트리를 통해 $O(logN * K)$ 의 시간복잡도로 풀어야 합니다. (1≤ N≤10^6 (N=원소의 개수), 1≤M,K≤10^4 (M= 업데이트 횟수))

  • 세그먼트 트리의 크기

    먼저 세그먼트 트리의 크기는 완전 이진트리인 점을 고려하여 $((1«ceil(logN))-1)$ 로 해도 되지만, ($ceil(log N)$ =세그먼트 트리의 높이), 보통 4N 정도의 크기로 설정해 줍니다. 다음은 4N 에 대한 증명입니다. (k*N에 대해서 𝑘<4인 수 중에 다른 수가 가능한지 궁금하다면 다음 링크를 보면 될것같습니다.)

    $𝑆(𝑛)\hspace{2mm}≤2^{⌈log_2𝑛⌉+1}−1$

    $\hspace{10mm}<2⋅2^{⌈log_2𝑛⌉}$

    $\hspace{10mm}=4⋅2^{⌈log_2𝑛⌉}−1$

    $\hspace{10mm}≤4⋅2^{⌊log_2𝑛⌋}≤4𝑛$

  • 세그먼트 트리 코드

    세그먼트 트리 코드는 3가지로 이루어져 있습니다. (1) initialize 하는 코드, (2) update하는 코드 (3) query(합)을 구하는 코드 입니다. 세그먼트 트리의 root node는 항상 1부터 시작해야 합니다. (완전 이진트리에서 자식의 번호가 2*i, 2*i+1이기 때문입니다.)

    • initialize

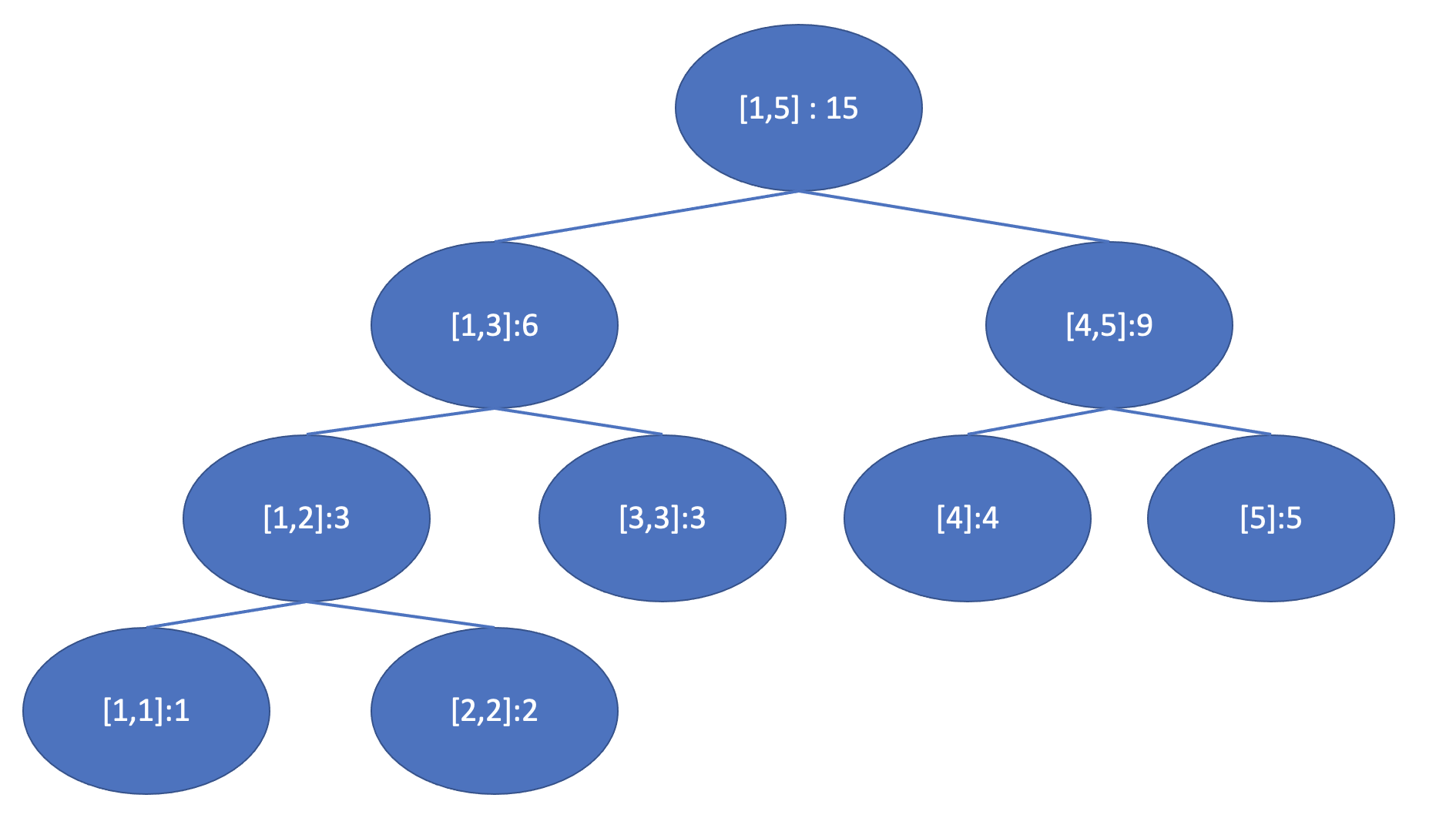
      Untitled

        ll init(int i,int l,int r){
      // 기저 사례
      if(l==r)
          return st[i]=a[l];
      int m = l+r>>1;
      return st[i]=init(i*2,l,m)+init(i*2+1,m+1,r);
  }

      n=5이고, 각 배열의 원소가 1,2,3,4,5인 것에 대해 위 그림처럼 트리가 만들어지게 됩니다.

    • update

        ll update(int i, int l,int r, int p, ll x) {
      if(p<l || p>r) // p가 이 구간에 포함되지 않음. 더이상 내려가지 않는다.
          return st[i];
      if (l == r) return st[i] = x;
      int m = l + r >> 1;

      return st[i] = update(i * 2,l,m,p,x) + update(i * 2 + 1, m + 1, r, p, x);
  }

      p번째 수를 x로 바꾸는 코드입니다. 해당 원소가 포함되는 구간들에 대해 모두 update해야 합니다.

    • query

        ll query(int i, int l,int r, int s, int e){
      if(e<l|| r<s) // 볼려고 하는 구간과 현재 구간이 전혀 겹치지 않는다.
          return 0;
      if(s<=l&&r<=e) // 완전히 포함 될때
          return st[i];
      int m=l+r>>1;
      return query(i*2,l,m,s,e)+query(i*2+1,m+1,r,s,e);
  }

      해당 하는 구간에 대해 합을 구하는 코드 입니다.

code 
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <cmath>
#define endl '\n'
#define INF 1e9
#define LINF 9223372036854775807
using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int> tup;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
priority_queue<tup,vector<tup>,greater<tup>> edge;

int t;
const int N = 1000001;
int a[N+1];
ll st[4*N];

// 관리하는 구간이 l에서 r까지
ll init(int i,int l,int r){
    // 기저 사례
    if(l==r)
        return st[i]=a[l];
    int m = l+r>>1;
    return st[i]=init(i*2,l,m)+init(i*2+1,m+1,r);
}
ll update(int i, int l,int r, int p, ll x) {
    if(p<l || p>r) // p가 이 구간에 포함되지 않음. 더이상 내려가지 않는다.
        return st[i];
    if (l == r)return st[i] = x;
    int m = l + r >> 1;

    return st[i] = update(i * 2,l,m,p,x) + update(i * 2 + 1, m + 1, r, p, x);
}
ll query(int i, int l,int r, int s, int e){
    if(e<l|| r<s) // 볼려고 하는 구간과 현재 구간이 전혀 겹치지 않는다.
        return 0;
    if(s<=l&&r<=e) // 완전히 포함 될때
        return st[i];
    int m=l+r>>1;
    return query(i*2,l,m,s,e)+query(i*2+1,m+1,r,s,e);
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    init(1,1,n); // 항상 1부터. 0으로 시작하면 * 2해도 안됨.,ㅣ

    for(int i=0;i<m+k;i++){
        ll a,b,c;
        cin>>a>>b>>c;
        if(a==1) update(1,1,n,b,c);
        else cout<<query(1,1,n,b,c)<<endl;
    }
}

B. 구간 합 구하기 2

10999번 구간 합 구하기

이 문제는 lazy propagation segment tree에 대한 내용입니다. 초기화 하는 부분은 같으나, 갱신에 대해서 느리게(lazy) 전파(propagation)하는 것을 적용해야 합니다.

구간 합 구하기와 구간 합 구하기2 의 차이점은 전자는 값을 갱신하는 부분이 i번째에서 일어났다면, 후자는 i번째부터 j번째까지의 구간이 갱신됩니다.

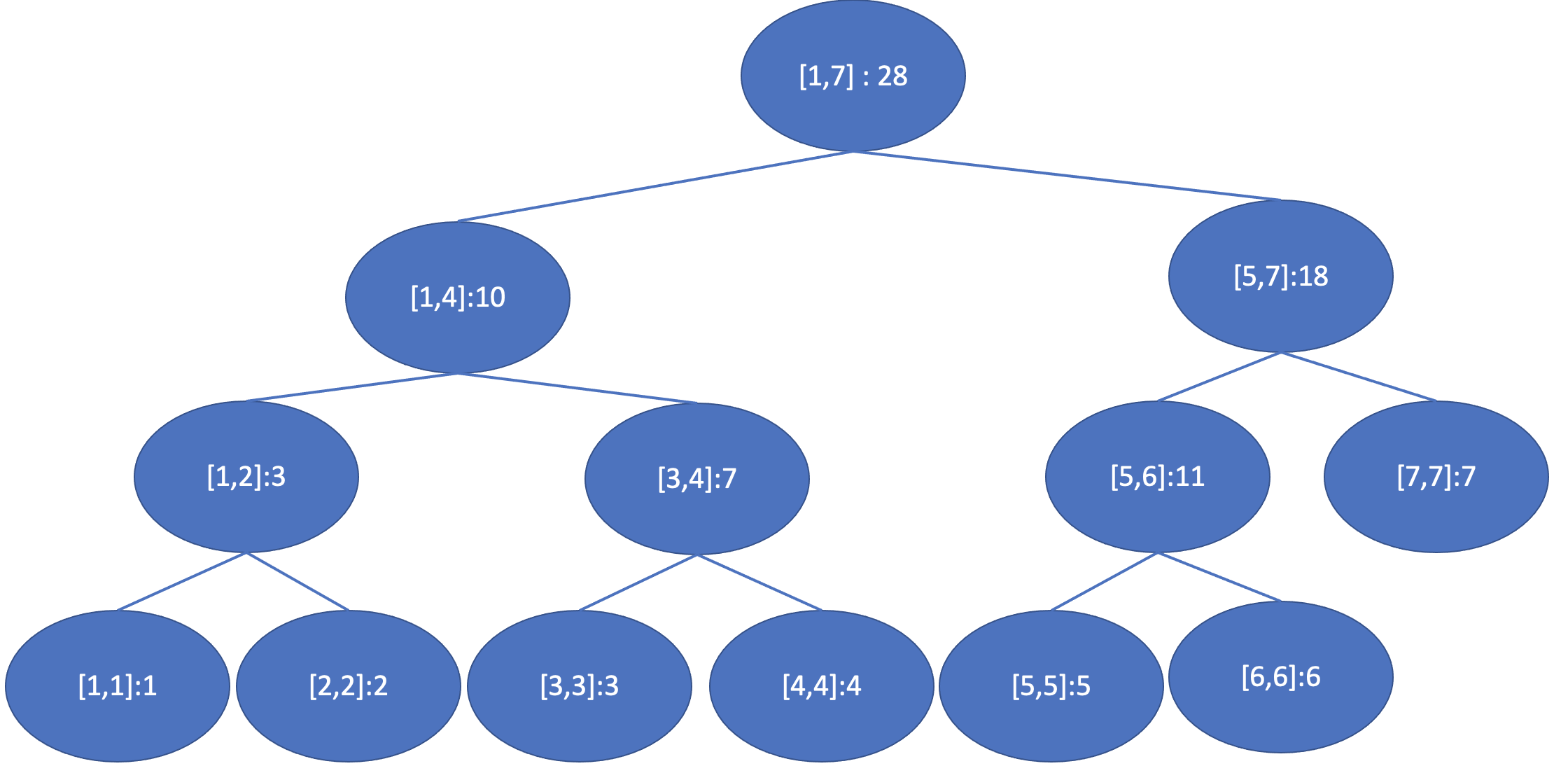
Untitled

만약 느리게 전파하지 않는 세그먼트로만 구현한다고 해봅시다. 위의 트리에 대해 2번째부터 6번째 원소까지 3을 더하여 갱신한다고 하면, 다음과 같이 갱신이 됩니다.

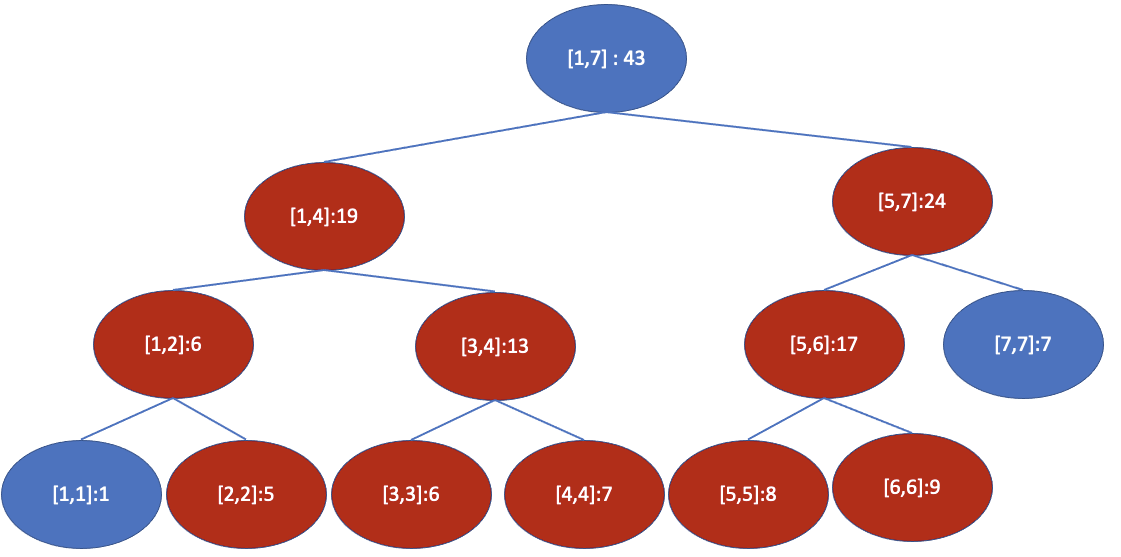
Untitled

하지만 이렇게 갱신을 하게되면, 갱신해야 하는 노드의 개수가 너무 많습니다. 모든 원소에 대해 다 갱신하는 방법은 시간초과가 납니다. 길이 N인 수열에서 하나의 수를 업데이트 하는데 $O(logN)$이 걸리므로, 최악의 경우 N개의 수에 대해 업데이트 한다면 $O(NlogN)$의 시간 복잡도가 걸리고, 갱신을 K번한다면 $O(NlogN * K)$으로 시간이 걸립니다.

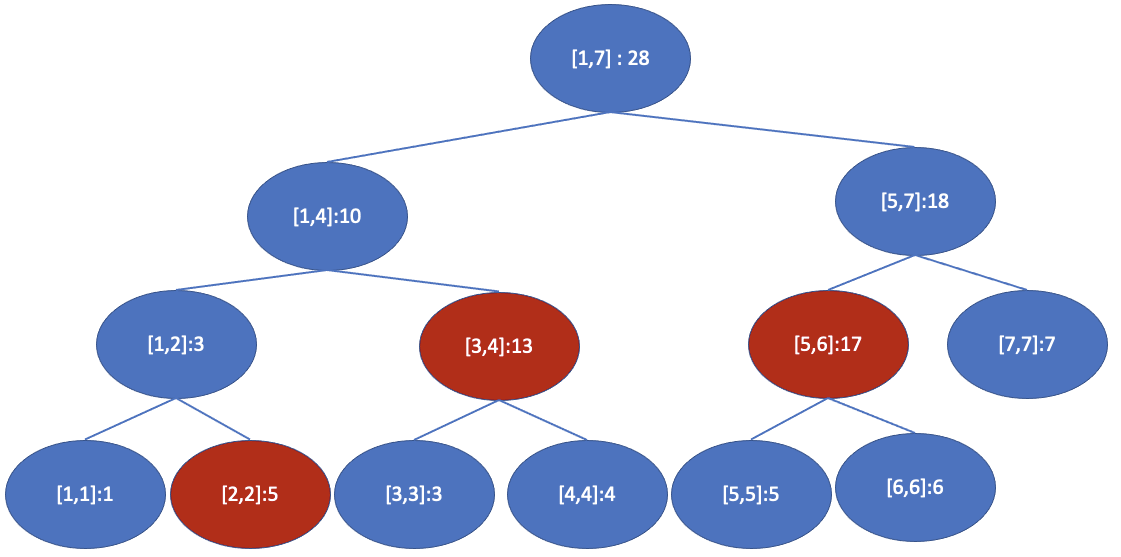
Untitled

그래서 위와 같이 갱신해야 하는 노드까지만 표시를 해주고 (구간에 해당되는 노드들), lazy propagation에 대한 트리를 따로 만들어서, 해당 원소 값을 직접 사용해야할때 계산해서 처리해줍니다. lazy propagation으로 구간 갱신을 하면 $O(logN * K)$ 의 시간복잡도를 갖게 됩니다.

현재 위의 트리라면 lz[10]~lz[13]에는 3이 들어가 있습니다. 만약에 [3,3] (10번 노드) 하나의 노드에 대해서만 propagation을 한다면 해당 노드들의 값이 업데이트가 되고, lz[10]는 0으로 초기화가 됩니다.

  • lazy propagation segment tree 코드
    • initiailize 하는 부분은 일반 세그먼트 트리와 동일합니다.

    • propagation

        void propagation(int i,int l, int r){
      if(lz[i]){
          st[i]+=(r-l+1) * lz[i];
          // 내려가지 않아도 지금 i번째 값을 내려갔다 올라온것처럼 계산할 수 있다.
          if(l!=r){
              lz[i*2]+=lz[i];
              lz[i*2+1]+=lz[i];
          }
          lz[i]=0;
      }
  }

      만약 해당하는 노드에 대해 갱신해야 할 값이 있다면 갱신해주고, 갱신을 해주었다면 0을 대입해줍니다. 예를들어 위의 트리에서 10번 노드([3,3])에 대해서 lz[10]=3이라고 해봅시다. propagation(10,3,3)을 실행하면 10번노드의 값에 3을 더해주고 lz[10]=0으로 초기화 해준 뒤에 연산이 끝납니다.

    • update code 
        ll update(int i, int l,int r, int s,int e, ll d) {
      propagation(i,l,r);
      if(e<l || s>r)
          return st[i];
      if (s<=l&&r<=e) {
          lz[i]+=d;
          propagation(i,l,r);
          return st[i];
      }
      int m = l + r >> 1;
      return st[i] = update(i * 2,l,m,s,e,d)+ update(i * 2 + 1,m + 1,r,s,e,d);
  }

      해당 구간에 대해 propagation할 것이 있으면 하고, 아니면 update합니다.

    • query

        ll query(int i, int l,int r, int s, int e){
      propagation(i,l,r);
      if(e<l|| r<s) // 볼려고 하는 구간과 현재 구간이 전혀 겹치지 않는다.
          return 0;
      if(s<=l&&r<=e) // 완전히 포함 될때
          return st[i];
      int m=l+r>>1;
      return query(i*2,l,m,s,e)+query(i*2+1,m+1,r,s,e);
  }

      해당 구간에 대해 propagation할 것이 있으면 하고, 아니면 구간합을 구합니다.

code 
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <map>
#include <set>
#include <cmath>
#define endl '\n'
#define INF 1e9
#define LINF 9223372036854775807
using namespace std;

typedef long long ll;
typedef pair<int, int> pi;
typedef tuple<int, int, int> tup;
ll gcd(ll a, ll b) { for (; b; a %= b, swap(a, b)); return a; }
priority_queue<tup,vector<tup>,greater<tup>> edge;

int t;
const int N = 1000001;
int a[N+1];
ll st[4*N];
ll lz[4*N];

// 관리하는 구간이 l에서 r까지
ll init(int i,int l,int r){
    // 기저 사례
    if(l==r)
        return st[i]=a[l];
    int m = l+r>>1;
    return st[i]=init(i*2,l,m)+init(i*2+1,m+1,r);
}
void propagation(int i,int l, int r){
    if(lz[i]){
        st[i]+=(r-l+1) * lz[i];
        // 내려가지 않아도 지금 i번째 값을 내려갔다 올라온것처럼 계산할 수 있다.
        if(l!=r){
            lz[i*2]+=lz[i];
            lz[i*2+1]+=lz[i];
        }
        lz[i]=0;
    }
}
ll update(int i, int l,int r, int s,int e, ll d) {
    propagation(i,l,r);
    if(e<l || s>r)
        return st[i];
    if (s<=l&&r<=e) {
        lz[i]+=d;
        propagation(i,l,r);
        return st[i];
    }
    int m = l + r >> 1;
    return st[i] = update(i * 2,l,m,s,e,d) + update(i * 2 + 1, m + 1, r, s,e,d);
}
ll query(int i, int l,int r, int s, int e){
    propagation(i,l,r);
    if(e<l|| r<s) // 볼려고 하는 구간과 현재 구간이 전혀 겹치지 않는다.
        return 0;
    if(s<=l&&r<=e) // 완전히 포함 될때
        return st[i];
    int m=l+r>>1;
    return query(i*2,l,m,s,e)+query(i*2+1,m+1,r,s,e);
}

int main(){
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    init(1,1,n); // 항상 1부터. 0으로 시작하면 * 2해도 안됨.,ㅣ
    for(int i=0;i<m+k;i++){
        ll a,b,c;
        cin>>a>>b>>c;
        if(a==1) {
            ll d;
            cin>>d;
            update(1, 1, n, b, c,d);
        }
        else cout<<query(1,1,n,b,c)<<endl;
    }
}

reference

(1) https://m.blog.naver.com/kks227/220791986409

(2) https://anz1217.tistory.com/33