(Winter 2021)CS224N|Lecture 9 Self- Attention and Transformers
20 Jan 2022
Lecture 목차
- RNN부터 attention based NLP model 복습.
- Transformer model 소개
- Great result with Transformers
- Drawbacks and variants of Transformers
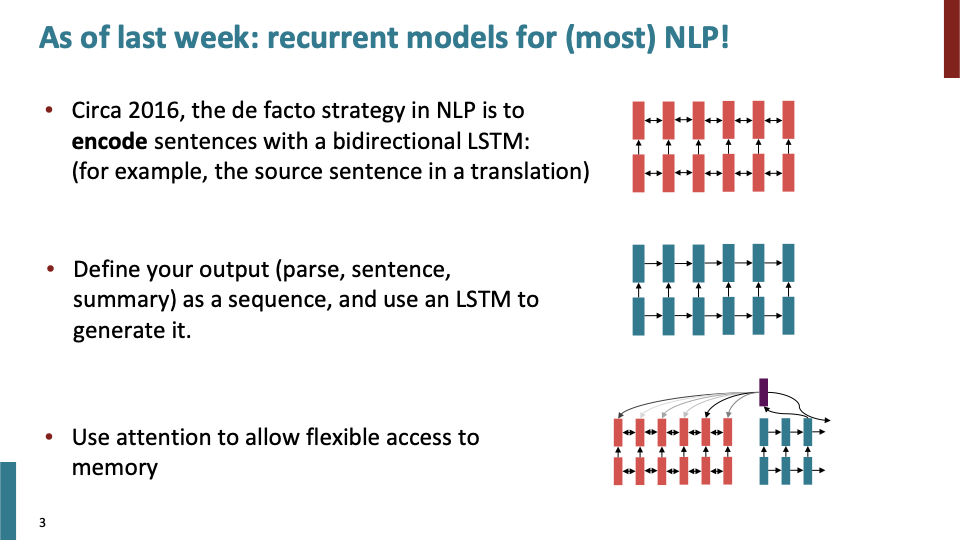 recap)Bidirectional LSTM, LSTM, Attention
recap)Bidirectional LSTM, LSTM, Attention
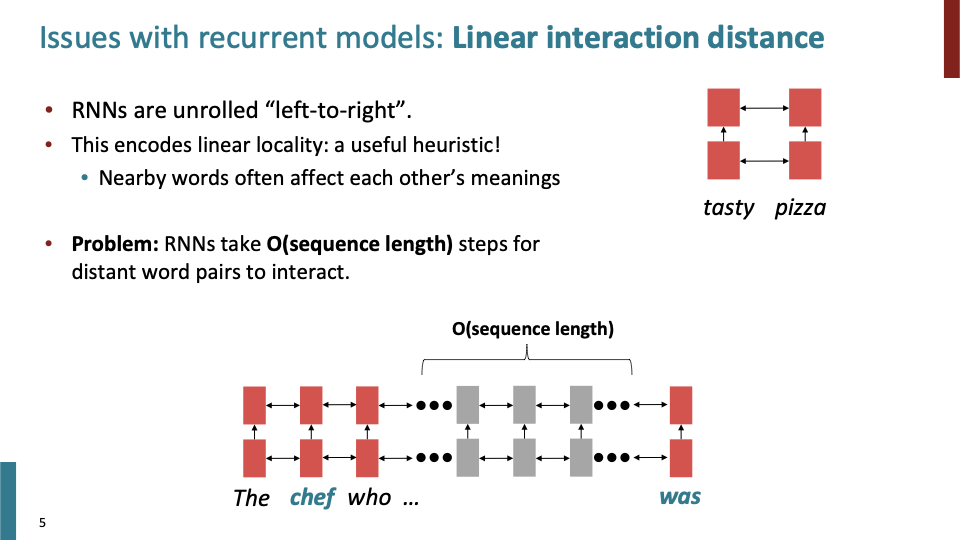 RNN은 linear locality를 Encode한다. 그래서 가까이 있는 word들이 서로에게 영향을 준다. 하지만 실제로는 단어들이 멀리 떨어져 있어도 서로 영향을 준다. (dependency parsing에서 이를 관찰할 수 있다.)
RNN은 linear locality를 Encode한다. 그래서 가까이 있는 word들이 서로에게 영향을 준다. 하지만 실제로는 단어들이 멀리 떨어져 있어도 서로 영향을 준다. (dependency parsing에서 이를 관찰할 수 있다.)
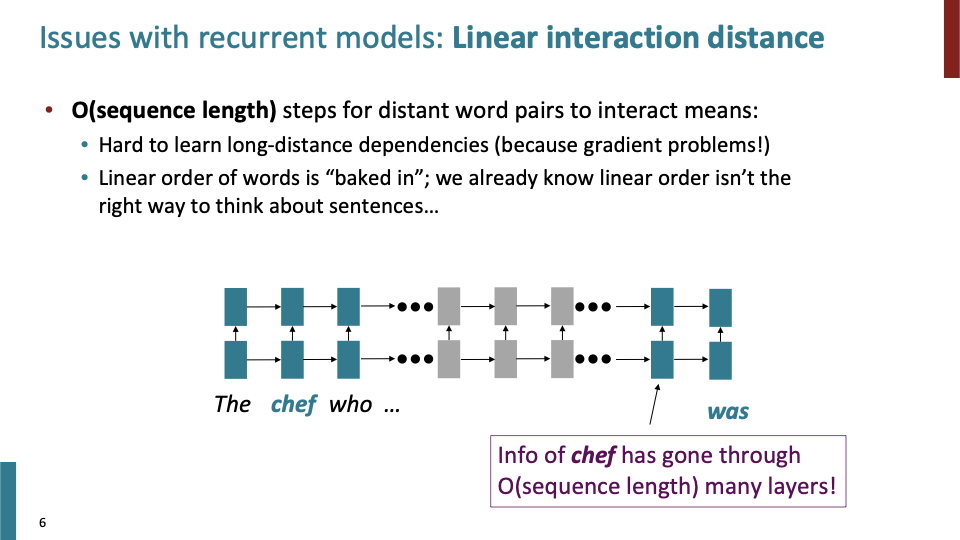
- long - distance dependency는 gradient 문제 때문에 학습되기 어렵다.
- 또한 linear한 순서로 단어들을 읽는 것은 올바른 방법이 아니다.
그래서 chief라는 단어가 was라는 단어를 만나기 까지 중간에 있는 recurrent weight matrix들을 계산해야한다.
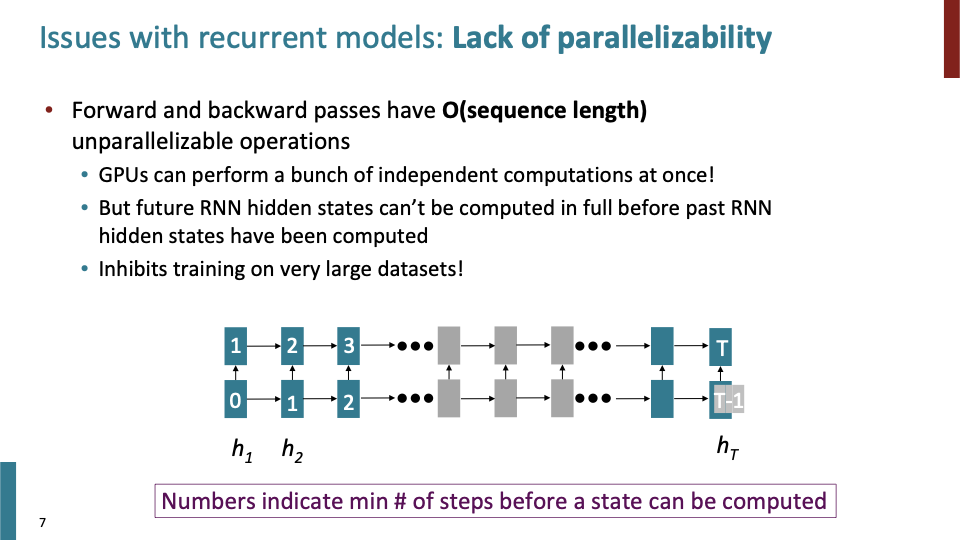 RNN을 동작시킬때, O(sequence length)개의 unparallelizable operation연산을 해야한다.
RNN을 동작시킬때, O(sequence length)개의 unparallelizable operation연산을 해야한다.
- GPU는 한번에 독립적인 연산(Vectorization!)을 여러개 할 수 있다.
- 하지만 RNN hidden state들은 explicit time dependence를 갖고 있기 때문에 병렬적으로 학습될 수 없다.
- 이것은 large dataset을 학습하는 데 있어서 좋지 않다. (하나씩 학습해야한다!)
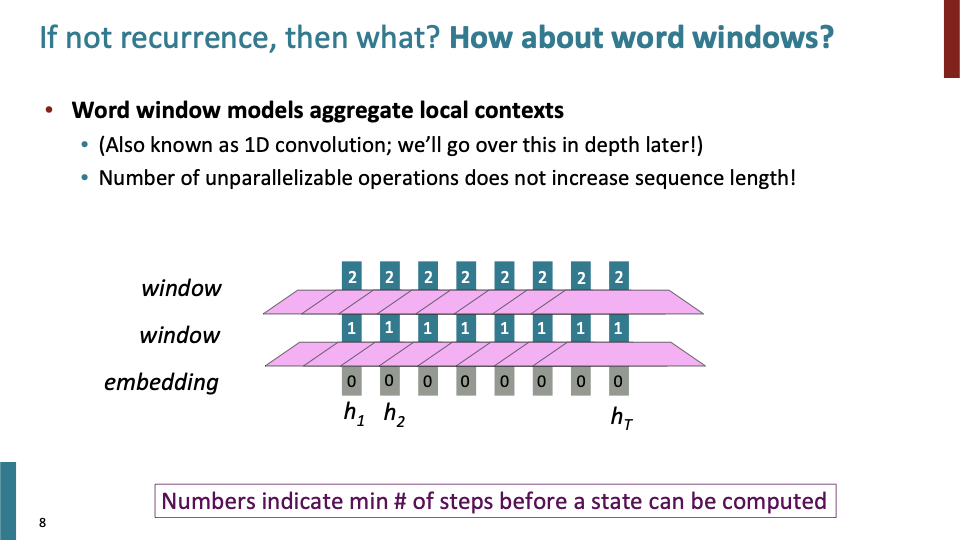
- word window model은 local context를 결합시켜서, center word에 대한 정보를 나타내는데 사용한다. 이것은 1D convolution이라고도 부른다.
- 각 단어를 각각 embedding에 들어가 있고, 각 단어에 대해 word window를 사용하면, 각 단어들은 모두 독립적인 연산을 하게된다. 즉 O(1) time dependency를 갖게된다.
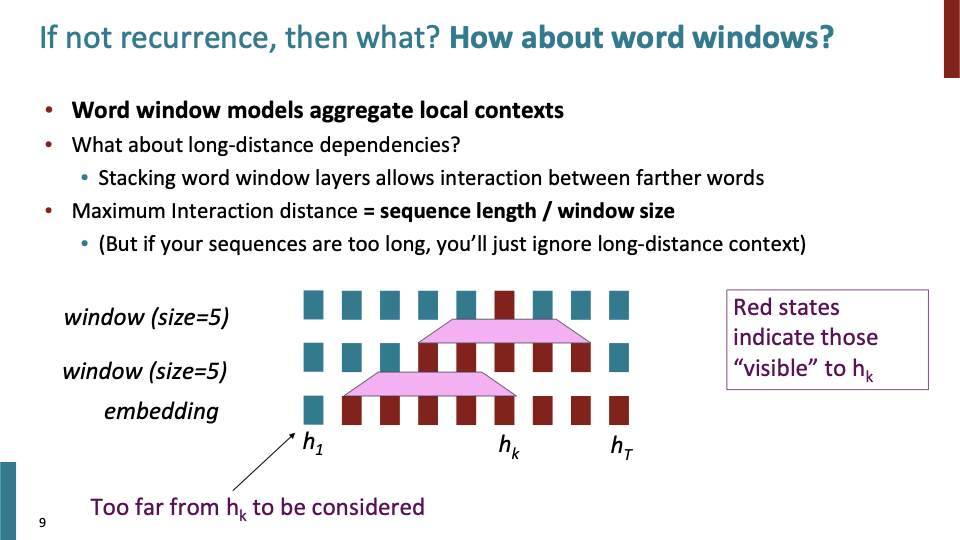
- word window는 Long-distance dependency를 알지 못한다. 하지만 word window를 stack하면 멀리 있는 단어들에 대해서도 고려할 수 있다.
- Maximum Interaction distance = sequence length / window size를 의미한다.
- 이 방법에도 문제가 있다. $h_k$를 학습할때, $h_1$에 대해서는 전혀 알지 못한다는 것이다. (더 깊게 더 넓은 window size를 사용하면 알 수 도 있긴하다.)
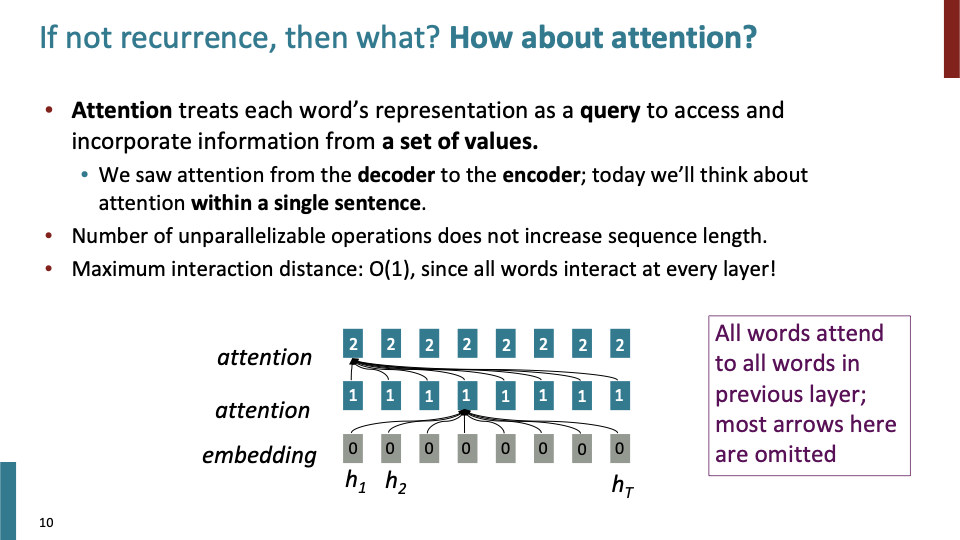
- attention에서 depth에 대해서 parallellize하게 학습하지는 못한다. 첫번째 layer를 학습해야 다음 layer로 넘어갈 수 있다. time에 대해서는 parallellize하게 학습할 수 있다. function of sequence length에 대해 O(1)이 걸리고, 각 단어의 interaction사이도 또한 O(1)이다.
- attention이 RNN의 두가지 문제점 (interaction하는데 sequence length만큼 걸렸고, time dependency하여 병렬학습 불가능했던것)을 해결했는지 보았다.
 그렇다면 이제 attention을 어떻게 building block으로 사용할지에 대해 생각해보자. 그 block이 self-attention이다.
그렇다면 이제 attention을 어떻게 building block으로 사용할지에 대해 생각해보자. 그 block이 self-attention이다.
- each query, key, value는 d차원의 vector이다.
- self-attention에서는 query q, key k, value v가 모두 같은 정보로부터 나온다하고, 이전 layer의 output을 x라하면 v=k=q=x이다. (모두 같은 정보로 부터 나오므로)
- dot product을 통해서 key-query affinity를 구한다.
- 그다음 softmax를 이용하여 weight들을 구한다.
- 마지막으로 weighted average를 구한다.
학생 Q) 이전 slide에서 볼 수 있듯이, connect every thing to every thing인데, 이것이 fully connected layer와 어떻게 다른가.
A) 전자에서 hidden state들이 어떻게 학습되는지 설명하기 어려운 반면, attention에서는 key와 query 사이의 interaction들을 학습하므로 어떻게 학습되는지 설명을 할수 있다. Actual strength of all the interactions, attention weight 와 같은 것을 학습할 수 있다. attention은 independent pairs of all connected thing을 배우는 것이 아니라 dot product과 같은 연산을 통해 parameter의 representation들을 학습한다. 정리하면 attention은 dynamic connectivity가 있다. (나중에 추가 설명)
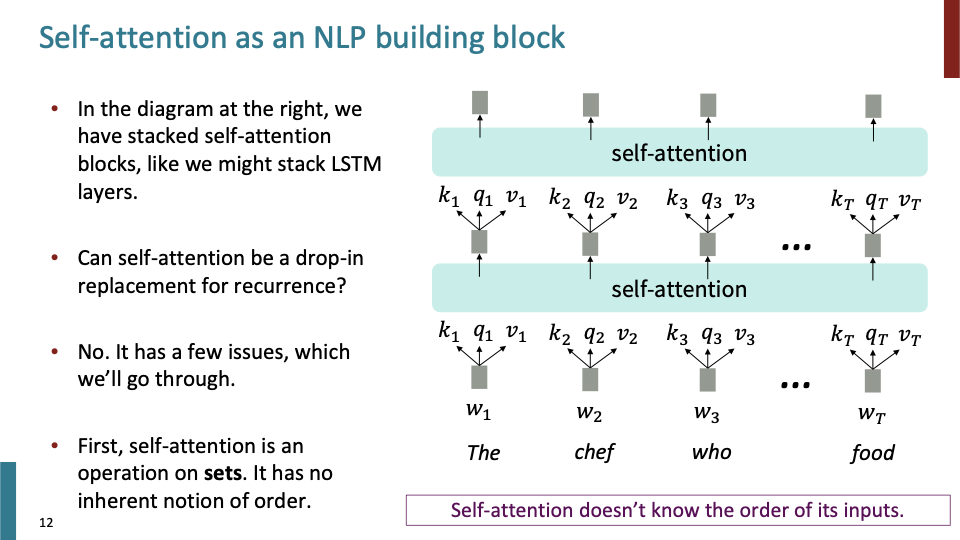 self-attention을 building block으로써 살펴보자. embedding으로부터 key, query, value를 얻는다.
self-attention을 building block으로써 살펴보자. embedding으로부터 key, query, value를 얻는다.
- self-attention은 sets을 대상으로 하는 연산이다. key, query, value에 대해서 indices와 같은 개념이 없다. 즉, self-attention은 순서를 고려하지 않는다. (이것이 첫번째 문제점)

- self-attention의 첫번째 문제인 sequence order를 해결 해야한다. 그래서 k,q,v안에서의 order를 파악해야한다.
- sequence 길이가 T이하라고 해보자. 1부터 T 사이의 값 i에 대해 $p_i$가 i번째 position vector를 뜻한다고 해보자. (뒤에 position vector에 대해서 설명). 그다음 k,v,q와 $p_i$를 더해서 $k_i, q_i, v_i$를 만든다. 이제 order를 안다고할 수 있다.

- position representation을 구현하는 방법은 sinusoid를 concatenation하는 것이다. 처음 transformer 논문이 나왔을 때, 이 방법을 사용했다.
- sinusoid들은 다양한 주기(period)를 갖는다. 각 row에 대해 다른 frequency(1/period)를 갖는다. sinusoid를 시각화한 위의 그림에서 vertical axis는 model의 dimensionality을 의미하고, horizontal-axis는 sequence length를 의미한다.
- Pros
- sinusoid는 periodicity를 갖기 때문에 different index마다 different value로 position을 표현할 수 있다. (이 period는 sequence length 보다는 아마 짧을 것이다. 모두 concatenation하기 때문에 각 sinusoid가 갖는 “absolute position”은 중요하지 않을 수 있다.)
- 그리고 longer sequence에 대해서도, period가 재시작하면 되기 때문에 position을 표현할 수 있다.
- Cons
- 하지만 concatenation된 sinusoid에는 learnable parameter가 없다.
- 또한 longer sequence에 대해 표현할 수 있다는 extrapolation도 잘 작동하지 않는다.

- 그래서 position vector의 모든 값을 learnable parameter으로 바꾼다. Matrix $p\in R^{d \times T}$이다. (위에서의 sinusoid와 dimensionality가 같다.)
- Pros
- position이 data에서 어떤 의미를 갖는 지에 따라 학습된다. 즉 flexibility가 있다.
- Cons
- index를 1부터 sequence length 이상으로 extrapolate 할 수 없다. Matrix P의 dimensionality를 $d\times T$라고 정해놓았다.
- 더 flexible한 representation of position과 관련된 work들이 있다. 위에서 말했다 시피, absolute index of word는 sentence에서의 natural representation of position이 아니기 때문이다.
- Representation of position이 없었다면 self-attention을 building block으로 사용할 수 없었을 것이다. 위에서 설명한 learnable parameter를 이용한 position representation으로 이 문제를 해결했다.
- 두번째 문제점은 단순히 weighted average를 계산하기 때문에 non-linearity가 없다. 이것에 대한 해결책을 알아보자.
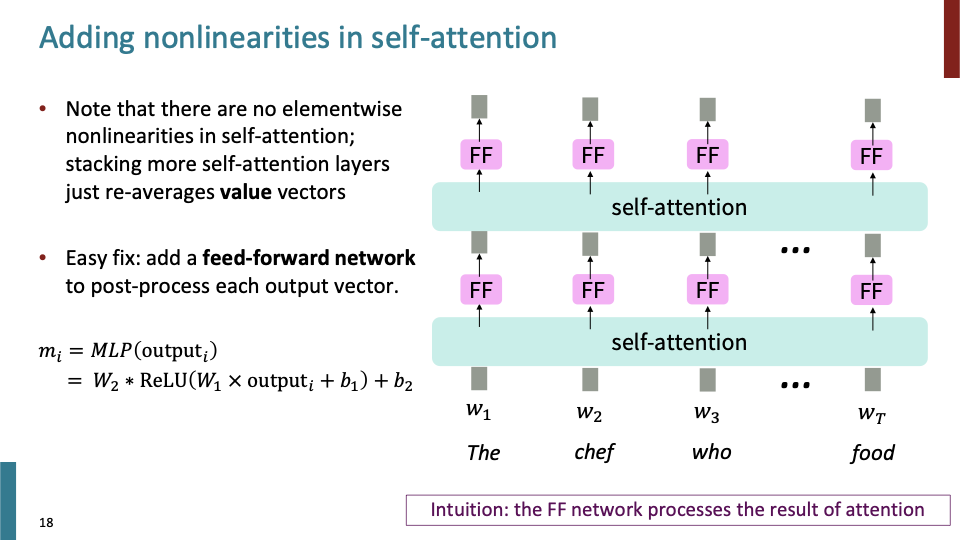
- self-attention layer를 계속 쌓아가며 계산하는 것은 결국엔 어떤 종류의 averagin projections of vectors를 하는 것과 같다. 그렇다면 각각의 단어 FF를 추가하면 어떨까. 같은 layer에 있는 FF NN들은 parameter들을 공유한다. 즉 Self-attention의 output에 feed-forward network를 추가하면 non-linearity문제를 해결할 수 있다.
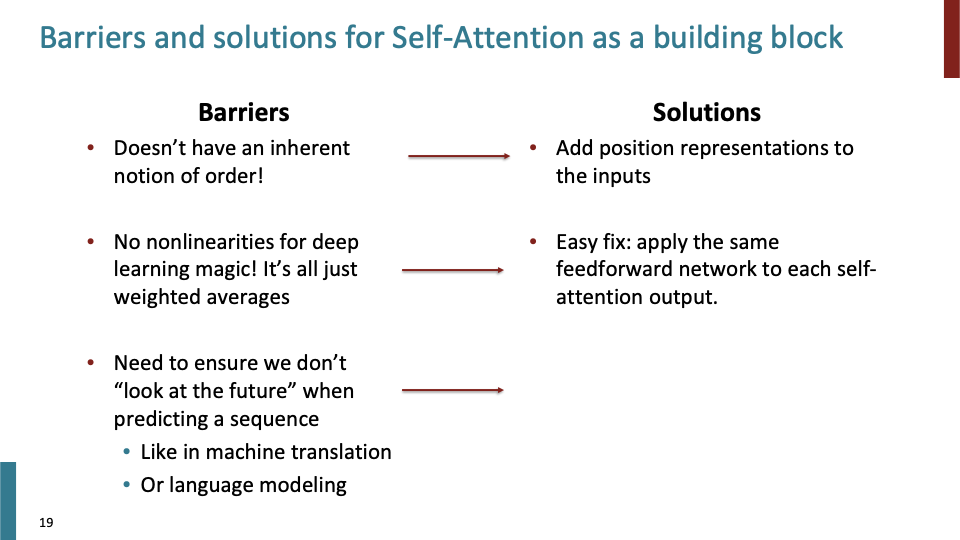
- 또 다른 문제점을 보자. Language Modeling을 할때, future에 있는 단어들을 보면 안된다. LM자체가 다음 단어를 예측하는 task이기 때문이다.
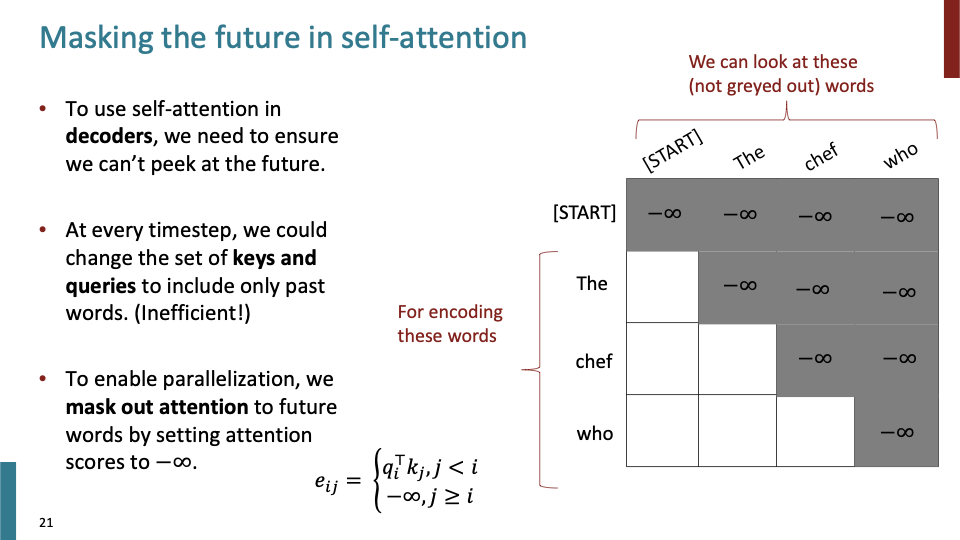
- 그래서 future에 있는 단어들을 모델이 보지 못하게 하기 위해 masking을 사용한다.
- Self-attention에서 decoder를 사용하기 위해 future를 masking한다. (encoder에서는 whole sentence를 볼 수 있다.)
- key, value (slide에 query라고잘못 들어간듯)들이 과거의 단어로만 이루어져 있게 동적으로 set을 변화시켜야 한다. 하지만 효율적이지 않다.
- parallelization을 이용하기 위해, attention을 mask한다. masking된 attention들에 minus infinity를 대입시켜 masking한다. 위의 수식 처럼 현재 position $i$ 이상의 position을 masking하는 것이다.
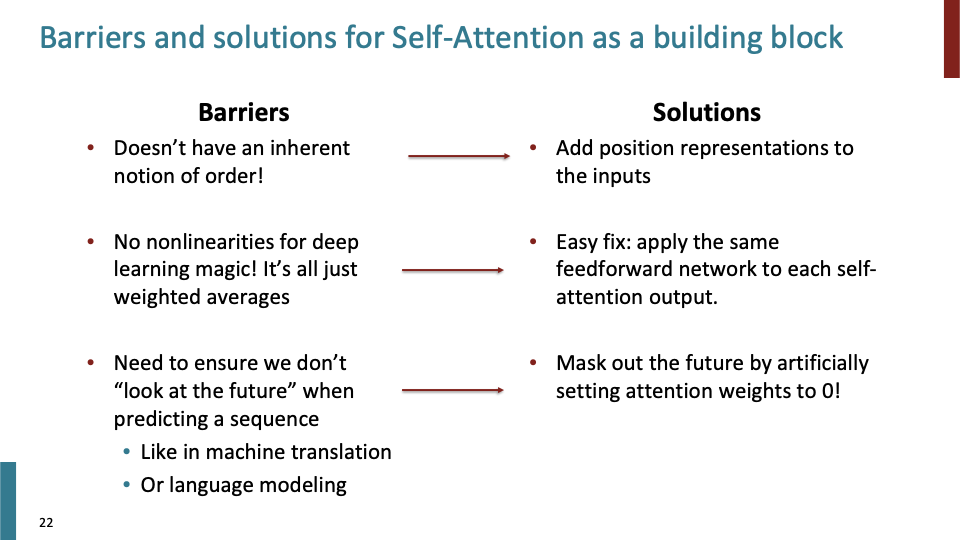
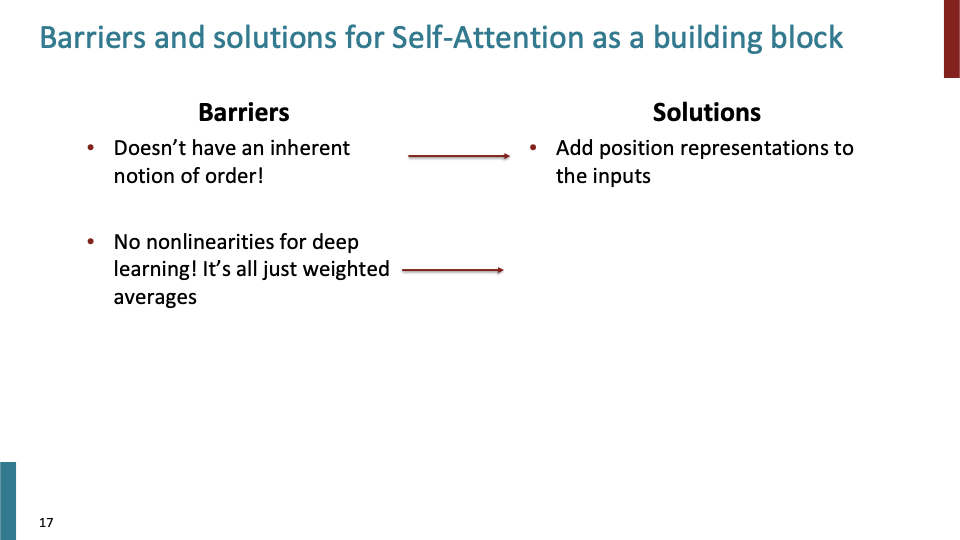
- order, nonlinear, future를 보는 문제점들에 위와 같이 해결했다. 이것들이 attention을 building block으로 사용하기 위해 알아야할 것들이다.
 앞서 말한 해결책을 정리한 내용이다. Non-linearity에 대해서 꼭 Feed-Forward network을 사용할 필요는 없다. 위의 내용들이 transformer를 활용하기 위해서 꼭 알아야 하는 것들이다. 이제 transformer model을 살펴보자.
앞서 말한 해결책을 정리한 내용이다. Non-linearity에 대해서 꼭 Feed-Forward network을 사용할 필요는 없다. 위의 내용들이 transformer를 활용하기 위해서 꼭 알아야 하는 것들이다. 이제 transformer model을 살펴보자.
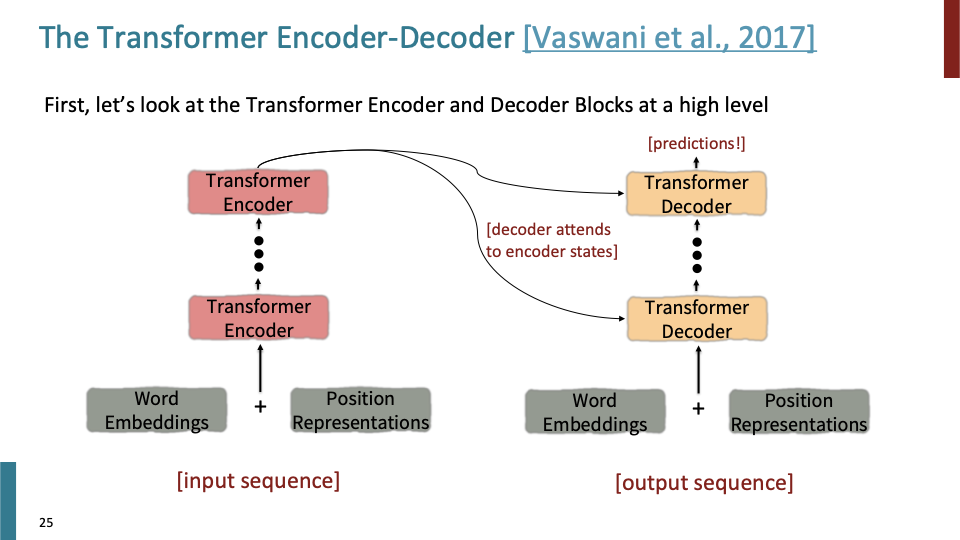 먼저 transformer의 encoder, decoder를 high level 관점에서 살펴보자. 그리고 각 building block들을 보자.
먼저 transformer의 encoder, decoder를 high level 관점에서 살펴보자. 그리고 각 building block들을 보자.
word embedding + position representation → embedding → transformer encoder → (decoder에도 embedding + position representation가 처음에 들어간다) transformer decoder (last layer of encoder가 모든 transformer decoder layer에 사용된다.) → predictions
앞서 배운 position representation, self-attention, decoder에서의 masking out 등의 component를 각 building block에 끼어 넣자!.
 이제 transformer를 이해하기 위해 더 알아야할 것들을 살펴보자.
이제 transformer를 이해하기 위해 더 알아야할 것들을 살펴보자.
- Key-Query-Value - attention : key, query, value를 single word embedding에서 어떻게 얻을까?
- Multi - headed attention : single layer에서 multiple place에 attend할 것이다.
- 그리고 학습할때 도움이 되는 여러가지 trick을 배울것이다. 이것들은 model 더 많은 것을 할 수 있게 해주는 것이 아니라, trainig process를 향상시켜주고, 이것들은 매우 중요하다.
- Residual connections
- Layer normalization
- Scaling the dot product

transformer Encoder에서는 key-query-value를 어떻게 구하는지 알아보자.
- $x_1,…,x_T$ : input vector in dimensionality $d$
- keys, queries, values
- $k_i =Kx_i$, $K\in R^{d \times d}$이고 $K$를 key matrix라 할것이다.
- $q_i =Qx_i$, $Q\in R^{d \times d}$이고 $Q$를 query matrix라 할것이다.
- $v_i =Vx_i$, $V\in R^{d \times d}$이고 $V$를 value matrix라 할것이다.
- 이전 slide에서는 x ( = input vector), k, q, v 모두 같다고 했지만 이제는 각각에 대응하는 matrix와 linear transformation을 하기 때문에 조금씩 다르다.
- 각각의 역할은 다르다. k, q 는 어딜 attend 해야 하는지 알려주고, v 는 다른 접근할 정보를 준다고 간단하게 말할 수 있다.
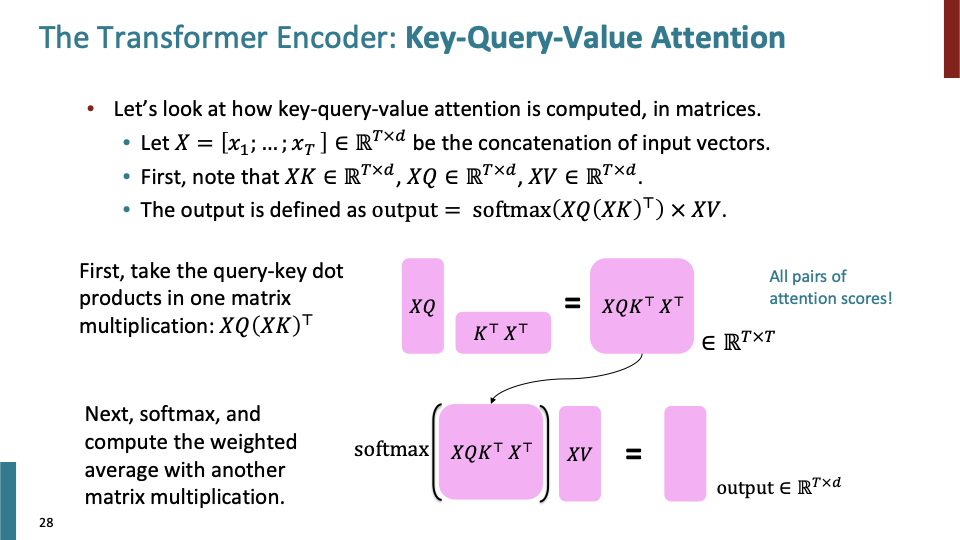
- In practice, 우리는 매우 큰 tensor를 다룬다. 그래서 input vector, key, query, value를 모두 matrix 형태로 바꾸어 쉽게 계산을 한다.
- 모든 input vector $x_i$를 $X=[x_1;…;X_T]\in R^{T\times d}$로 만든다.
- $d\times d$ transformation을 하기 때문에 $XK$, $XQ$, $XR$이 모두 $R^{T\times d}$ dimensionality를 갖는다.
- Output을 어떻게 계산하는지 살펴보자.
- query-key dot prodcut : $XQ(XK)^T \in R^{T\times T}$
- softmax를 통해 weighted average를 계산하고, 그 결과를 $XV$와 dot product하여 $\in R^{T\times d}$의 dimensionality output를 갖게 된다.

- 이제, Transformer에서 많이 중요한 Multi-headed attention을 살펴보자. 어떻게 sentence의 multiple place를 한번에 attend할까? normal self-attention으로도 가능하지만, self-attention은 결국ㅇ에 $x_i^T Q^TKx_j$가 높은 값을 갖는 place을 볼것이다. 만약 다른 place j를 어떠한 이유로 focus하고 싶다면 어떻게 해야하나.
- 그래서 multi attention heads라는 것을 multiple Q,K,V를 통해 정의한다. 이것들을 $x_i$에 대해 다른 것들을 encode하고, different transformation을 학습한다. single Q, single K, single V 대신에 우리는 sub Q, sub K, sub V를 이용한다. (sub = 부분 집합) $Q_l,K_l,V_l \in R^{d\times{d \over h}}$의 dimensionality를 갖는다. h는 attention head의 개수, l은 1부터 h까지 중의 값을 의미한다.
- 이것들을 softmax에 넣어 $V_l$과 곱해주면 output이 다음과 같이 계산 된다. $output_l =softmax(XQ_l^TK_l^TX^T)XV_l \in R^{d\over h}$. 모든 head (h개)의 output을 concatenate시켜서 total output $Y\in R^{d\times d}$을 만든다.
- 각 attention head는 독립적으로 동작한다.
- 그리고 output dimensionality와 input dimensionality를 동일하게 만들기 위해 output을 모두 concatenate시킨다.
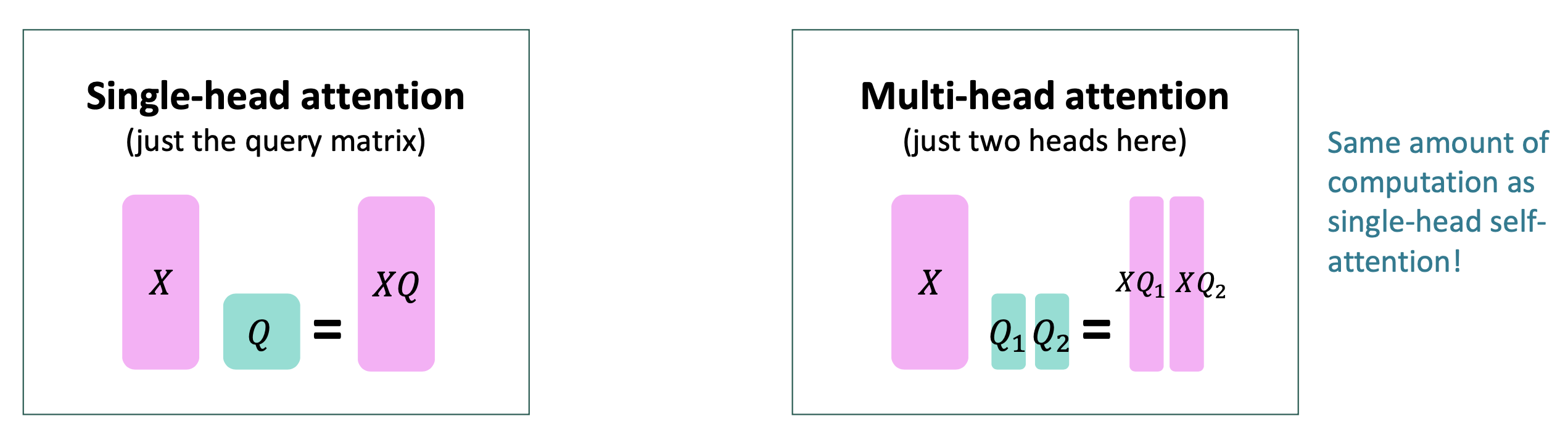
- Multi-head attention일지라도 single-head보다 더 많은 일을 하지 않는다. multi-head attention의 Q,K,V vector들은 single보다 lower dimensionality를 갖는것을 참고하자.
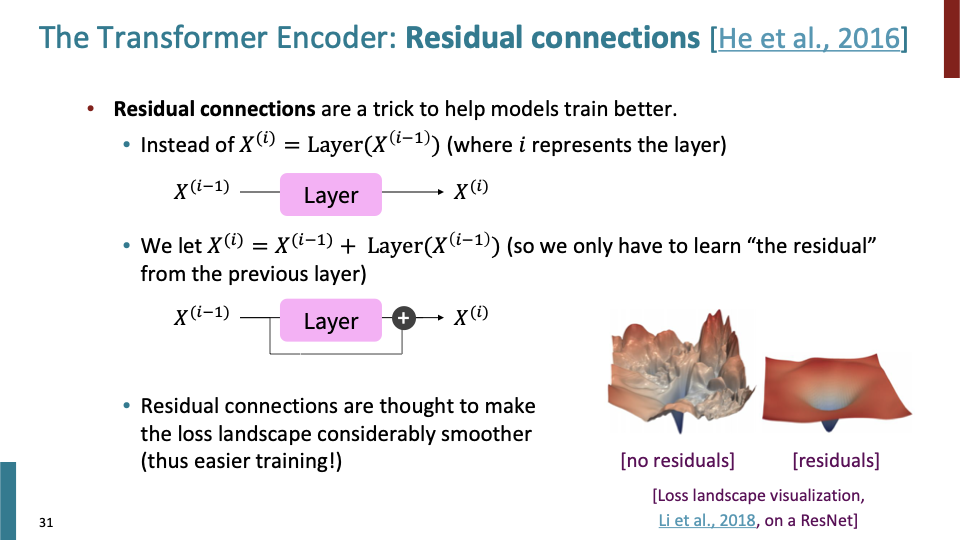 첫번째 training trick인 Residual connection에 관한 것이다.
첫번째 training trick인 Residual connection에 관한 것이다.
- i 는 network에서의 depth를 의미한다.
- Residual connection은 간단하다. $X^{(i)}=X^{(i-1)}+Layer(X^{(i-1)})$이다.
- $X^{(i-1)}$은 Inductive bias로써, layer($X^{(i-1)}$)로부터 학습한 것이 이전 output과 어떻게 달라야 하는지 정보를 줄 수 있다.
- 또한 vanishing gradient 관해서 layer안에서 vanishing된다 하더라도, residual connection을 통해 gradient가 propagate될 수 있다.
- 또한 Residual connection이 loss를 더 smoother하게 만들어 더 쉽게 학습할 수 있다. slide의 그림이 Residual connection 유무에 따른 loss landscape visualization 이다.
 두번째 trick인 Layer normalization에 대해 간단하게 말하면 다음과 같다. forward pass된 hidden vector들중 training에 손상시킬 수 있는 uninformative variation을 layer normalization을 이용해 cut down해보고자 하는 것이다. Layer의 hidden vector mean, std를 계산하여 layer normalization하는 것이다.
두번째 trick인 Layer normalization에 대해 간단하게 말하면 다음과 같다. forward pass된 hidden vector들중 training에 손상시킬 수 있는 uninformative variation을 layer normalization을 이용해 cut down해보고자 하는 것이다. Layer의 hidden vector mean, std를 계산하여 layer normalization하는 것이다.
 세번째 trick인 scaled dot product이다. 말 그대로 dot product을 scaling하는 것이다. dimensionality가 증가하면, dot product의 결과의 dimension도 증가한다. 그 결과가 directly softmax로 들어가면 softmax가 매우 peaky한 shape (대부분의 값들이 매우 작은값)을 갖게되고, gradient가 작아진다. softmax는 hidden vector의 weight을 만드는 역할을 하는데, 대부분의 weight들이 0이되면 attend하는 효과가 나타나지 않을 것이다. 그래서 $\sqrt{d/h}$로 scaling해준다.
세번째 trick인 scaled dot product이다. 말 그대로 dot product을 scaling하는 것이다. dimensionality가 증가하면, dot product의 결과의 dimension도 증가한다. 그 결과가 directly softmax로 들어가면 softmax가 매우 peaky한 shape (대부분의 값들이 매우 작은값)을 갖게되고, gradient가 작아진다. softmax는 hidden vector의 weight을 만드는 역할을 하는데, 대부분의 weight들이 0이되면 attend하는 효과가 나타나지 않을 것이다. 그래서 $\sqrt{d/h}$로 scaling해준다.
Q 학생 질문) decoder attention에서, first layer에 대해서만 masking하는 것인가 아니면 middle layer에 대해서도 masking하는 것인가.
A) 당연하게도, decoder의 모든 single layer가 masking을 한다. encoder의 모든 state를 볼 수 있고, decoder에서는 masking으로 인해 previous words에 대해서만 볼 수 있다.
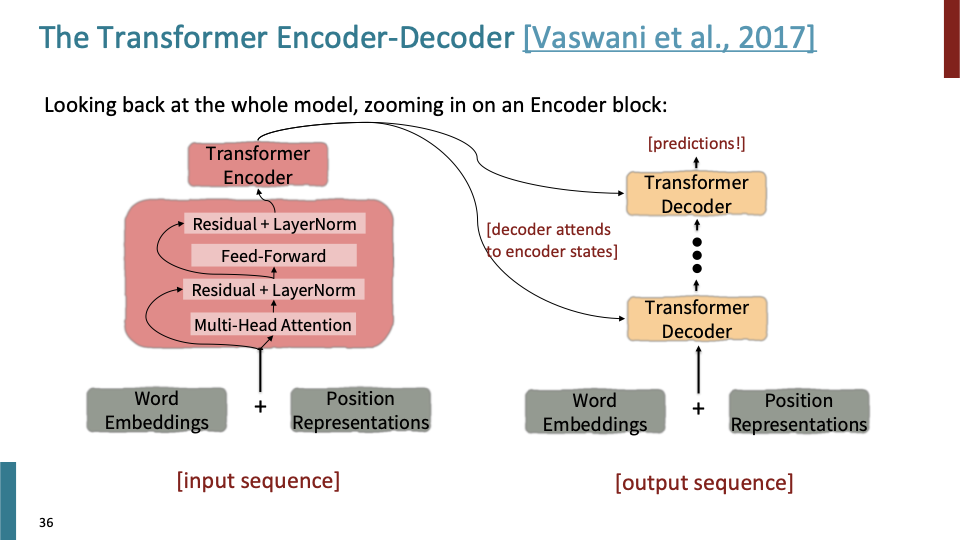 위 슬라이드에서 배웠던것들을 encoder 모델에 넣으면 위와 같다. Encoder의 각 layer가 저 확장된 block과 동일한 block으로 이루어져 있다.
위 슬라이드에서 배웠던것들을 encoder 모델에 넣으면 위와 같다. Encoder의 각 layer가 저 확장된 block과 동일한 block으로 이루어져 있다.
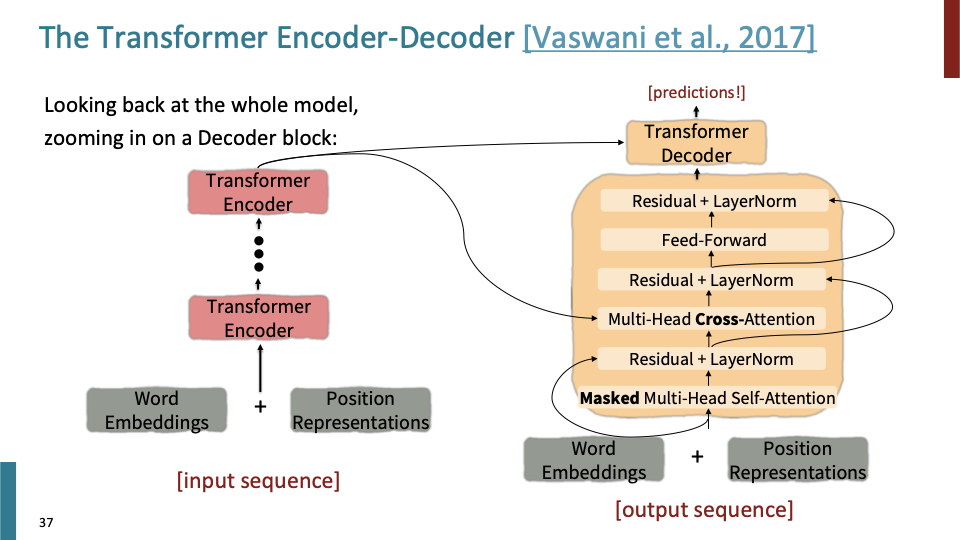 일단 Encoder와 다르게 Masking이 추가되어 있다. 또 다른 것은 Multi-Head Corss-Attention이다. 이 구조는 attetion과 매우 유사하다. (attention에서는 decoder의 각 block이 encoder의 모든 input vector에 attend한다.) decoder의 각 block에는 2개의 attention function이 있다.
일단 Encoder와 다르게 Masking이 추가되어 있다. 또 다른 것은 Multi-Head Corss-Attention이다. 이 구조는 attetion과 매우 유사하다. (attention에서는 decoder의 각 block이 encoder의 모든 input vector에 attend한다.) decoder의 각 block에는 2개의 attention function이 있다.
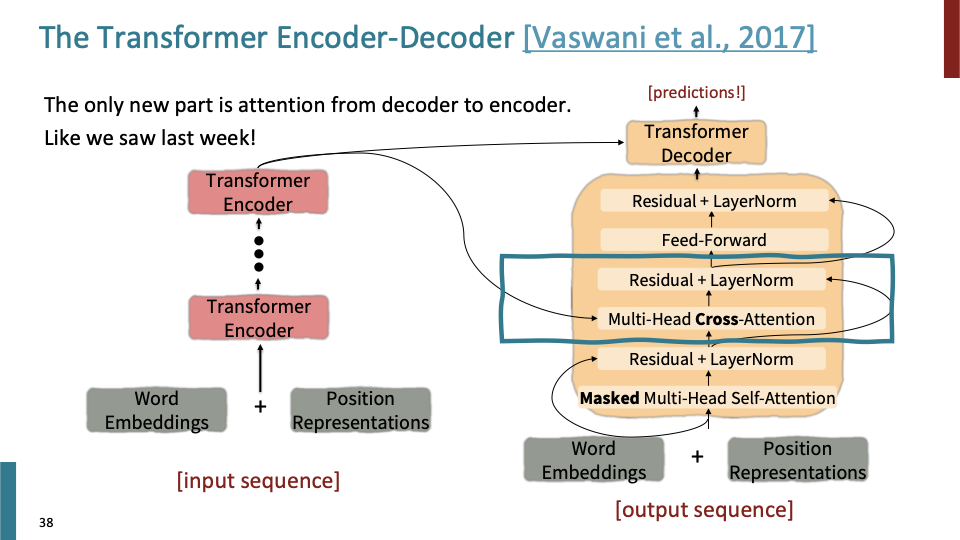 우리 수업에서 아직 살펴보지 않은 내용이 Multi-head cross attention이다. mutli-head self attention과 동일한 equation이지만, input이 다른 곳(encoder의 last output)으로 부터 들어오기 때문에 자세히 다뤄보려 한다.
우리 수업에서 아직 살펴보지 않은 내용이 Multi-head cross attention이다. mutli-head self attention과 동일한 equation이지만, input이 다른 곳(encoder의 last output)으로 부터 들어오기 때문에 자세히 다뤄보려 한다.
 Self attention에서는 keys, queries, values가 모두 같은 source로부터 들어 왔다. decoder의 Cross-attention에는 Transformer encoder의 마지막 output $h_1,…,h_T$가 $k_i=Kh_i, v_i=Vh_i$에 사용되고, decoder의 input은 query를 계산하는 $q_i = Qz_i$에 사용된다.
Self attention에서는 keys, queries, values가 모두 같은 source로부터 들어 왔다. decoder의 Cross-attention에는 Transformer encoder의 마지막 output $h_1,…,h_T$가 $k_i=Kh_i, v_i=Vh_i$에 사용되고, decoder의 input은 query를 계산하는 $q_i = Qz_i$에 사용된다.
이 방식이 memory에 access하는 것과 유사하다. value들로 이루어진 memory를 key를 통해 접근할 수 있고, query는 그 얻어진 데이터로 무엇을 볼지 결정한다. 즉 encoder를 메모리처럼 생각하면, encoder에서 얻어진 데이터를 decoder에서 어떻게 사용할지 결정하는 것이다.
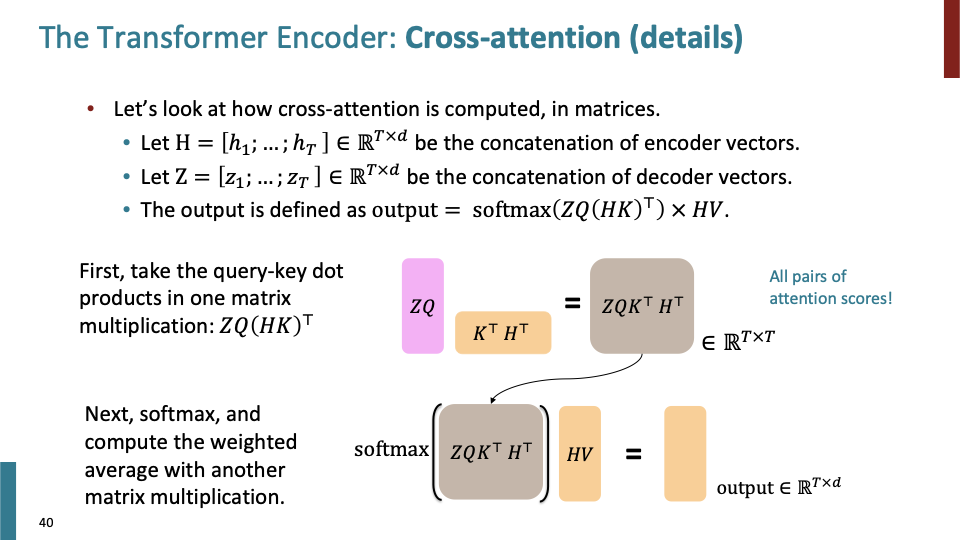
- Z for Query, H for Key , Value.
 Transformer의 결과를 살펴보자.
Transformer의 결과를 살펴보자.
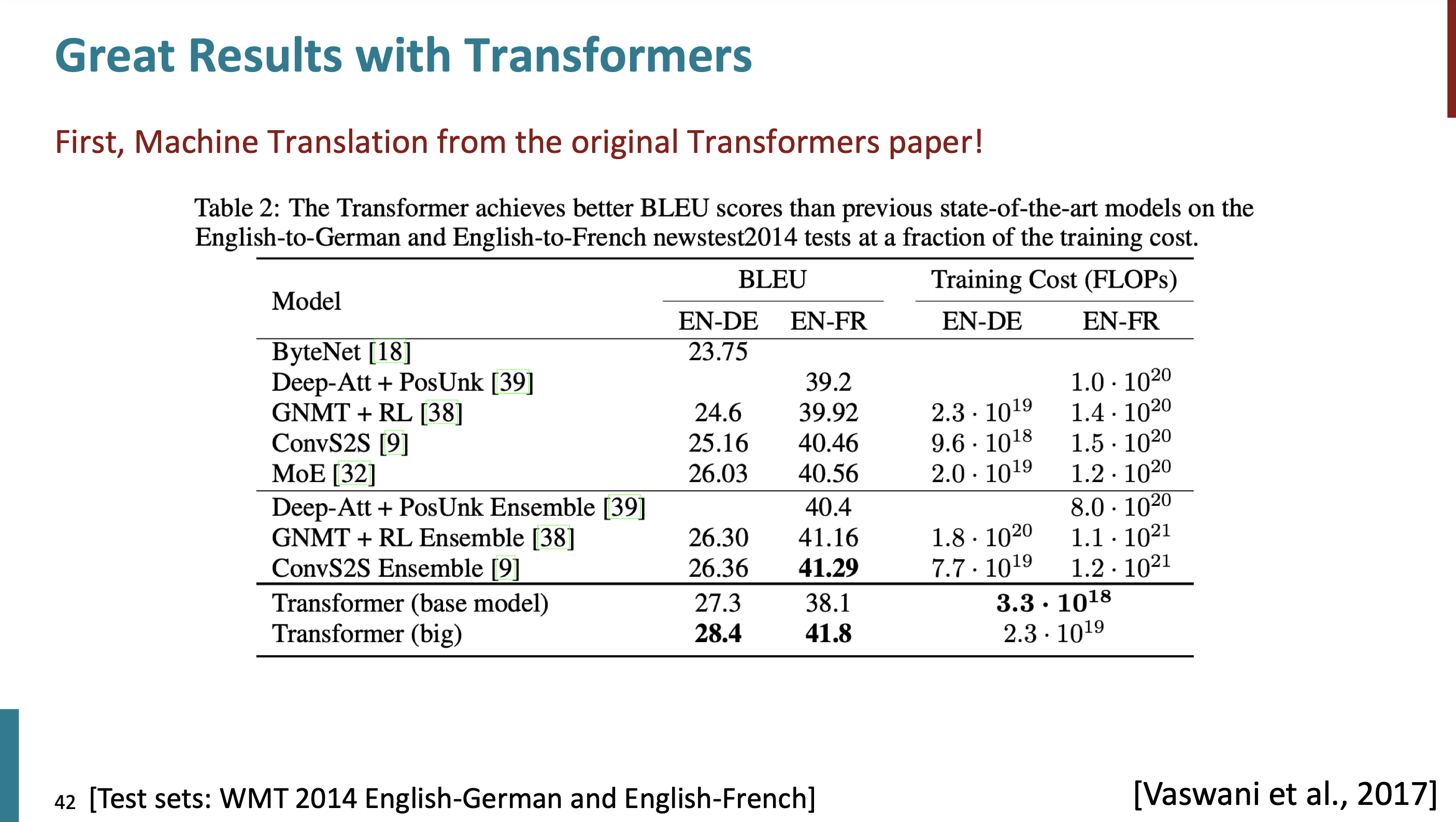
Attention is all You need paper에 있는 table이다.
 perplexity는 낮아질 수 록 좋은것이다. ROUGE-L에 대해서는 높을 수 록 좋은것이다.
perplexity는 낮아질 수 록 좋은것이다. ROUGE-L에 대해서는 높을 수 록 좋은것이다.

- 사실 transformer은 parallelizability 때문에 더 dominant한 모델이 되었다. ton of data로 매우 빠르게 pretraining할 수 있게 해준다. 다음 강의에서 pretraining을 다룰 것이다.
- GLUE라는 benchmark dataset의 ranking에 있는 모델들은 모두 transformer base이다. 그 이유는 근본적으로 transformer의 pretrain-ability 때문이다.
학생 질문 Q1) scaling dot product과 관련된 질문이다. 왜 그냥 $h\over d$가 아닌 $\sqrt {h\over d}$로 나눴는지에 대한 질문이었다. (또는 다른 function(d/h)가 아니라)
A1) paper에 명시되어 있다. ! (까먹었다고 한다.) 학생 질문
Q2) layer norm하기 전에 값이 매우 작으면, norm을 적용시킨 값이 문제가 되지 않는가?
A2) layer normalization은 모든 것을 averaging out(=normalization)하지만, 그것이 vector들을 매우 작게 만드는 것은 아니다. 라고 조교가 설명했고, 교수님은 다른 답을 말햇다. 작은 값을 normalization하면 dynamic range와 관련된 것을 Loss을 잃을 것이고, scaling을 통해 해결해야 할 것이다.
 이제 transformer의 문제점에 대해 살펴보자.
이제 transformer의 문제점에 대해 살펴보자.
 self-attention의 연산 복잡도는 sequence length에 Quadratic하다. recurrent model은 linear하게 grow한다.
self-attention의 연산 복잡도는 sequence length에 Quadratic하다. recurrent model은 linear하게 grow한다.
Self-Attention의 시간복잡도 $O(n^2d)$, Recurrent에서 $O(nd^2)$이라는 시간복잡도 라는 얘기가 paper에 나온다. ( n = sequence length)
 Practice에서는 sequence length T는 보통 512정도의 값을 갖는다. 하지만 만약 T≥10000의 long document에 대해 학습할까. 어떠한 방법으로든 $T^2$를 최적화 시켜야한다.
Practice에서는 sequence length T는 보통 512정도의 값을 갖는다. 하지만 만약 T≥10000의 long document에 대해 학습할까. 어떠한 방법으로든 $T^2$를 최적화 시켜야한다.
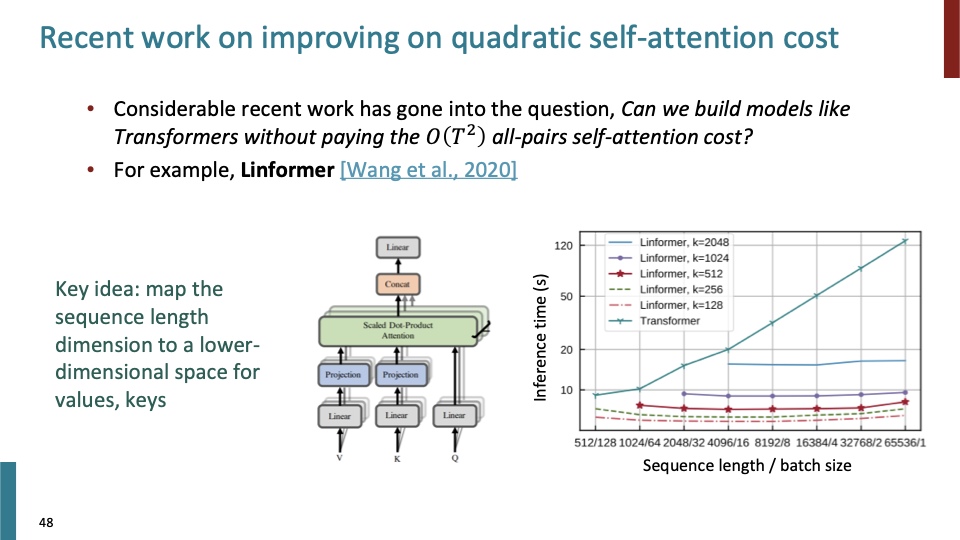 위의 문제점에 대한 한가지 해결책은 Linformer이다. key idea는 sequence length dimension을 lower dimension space로 mapping 시키는 것이다.
위의 문제점에 대한 한가지 해결책은 Linformer이다. key idea는 sequence length dimension을 lower dimension space로 mapping 시키는 것이다.
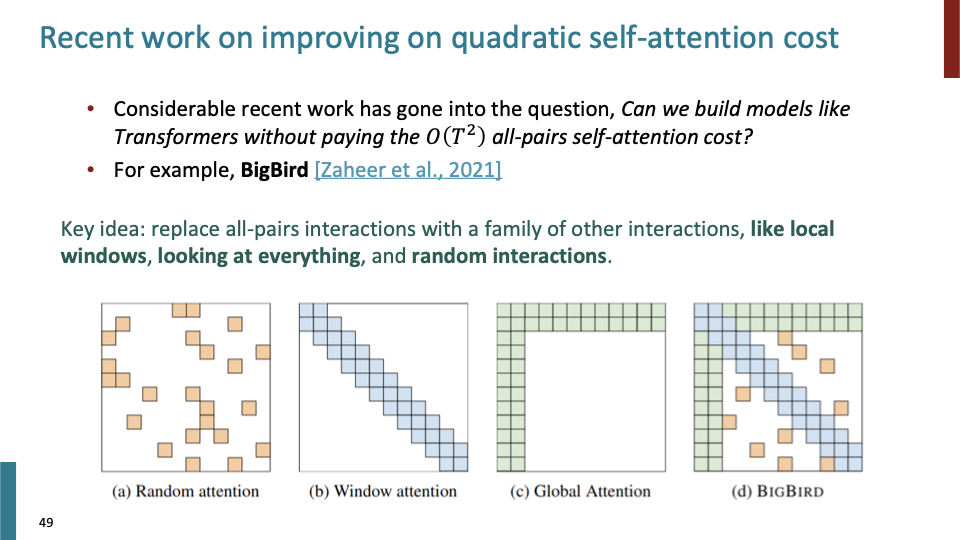 완전히 다른 접근방법으로, all-pairs interaction을 고려하지 말자는 것이다. all-pairs interaction을 하는 것보다 다른 더 효율적인 방법으로 이를 골려해보자는 것이다. 예를들어 local window, looking at everything, random interaction.
완전히 다른 접근방법으로, all-pairs interaction을 고려하지 말자는 것이다. all-pairs interaction을 하는 것보다 다른 더 효율적인 방법으로 이를 골려해보자는 것이다. 예를들어 local window, looking at everything, random interaction.
BigBird는 이런 것들을 모두 합쳐서, all-pair interaction과 유사한 결과를 얻을 수 있다고 한다.