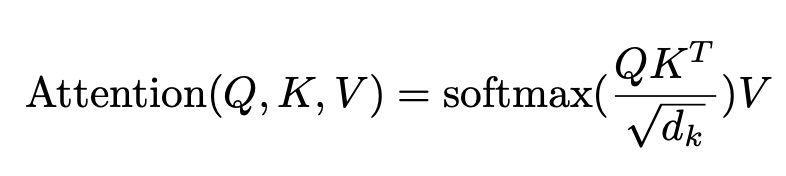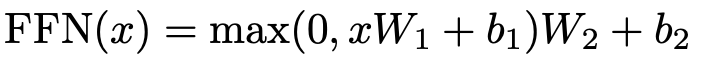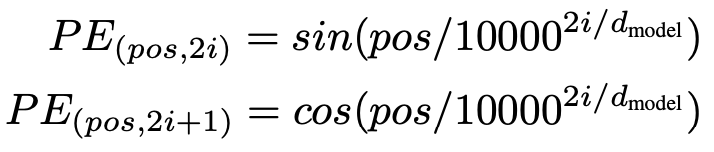Attention Is All You Need

Natural Language Processing • Paper

20 Jan 2022

Comments

구현하고자 하는 sequence recommendation model ‘Self-Attentive Sequential Recommendation’이 transformer기반으로 되어 있어서 Attention Is All You Need 을 읽게 되었다. 이번 기회에 transformer를 parallelization 하는것 까지 pytorch로 구현해보고자 한다. 2021 winter cs224n lecture 9 포스트를 이 논문 review이후에 올렸는데, 그 포스트를 보면 transformer까지 진행된 flow와 모델의 component에 대한 근거를 더 명확하게 이해할 수 있을것 같다.

해당 논문에 대해 transformer repository에 구현해보고 있습니다.

---

Abstract

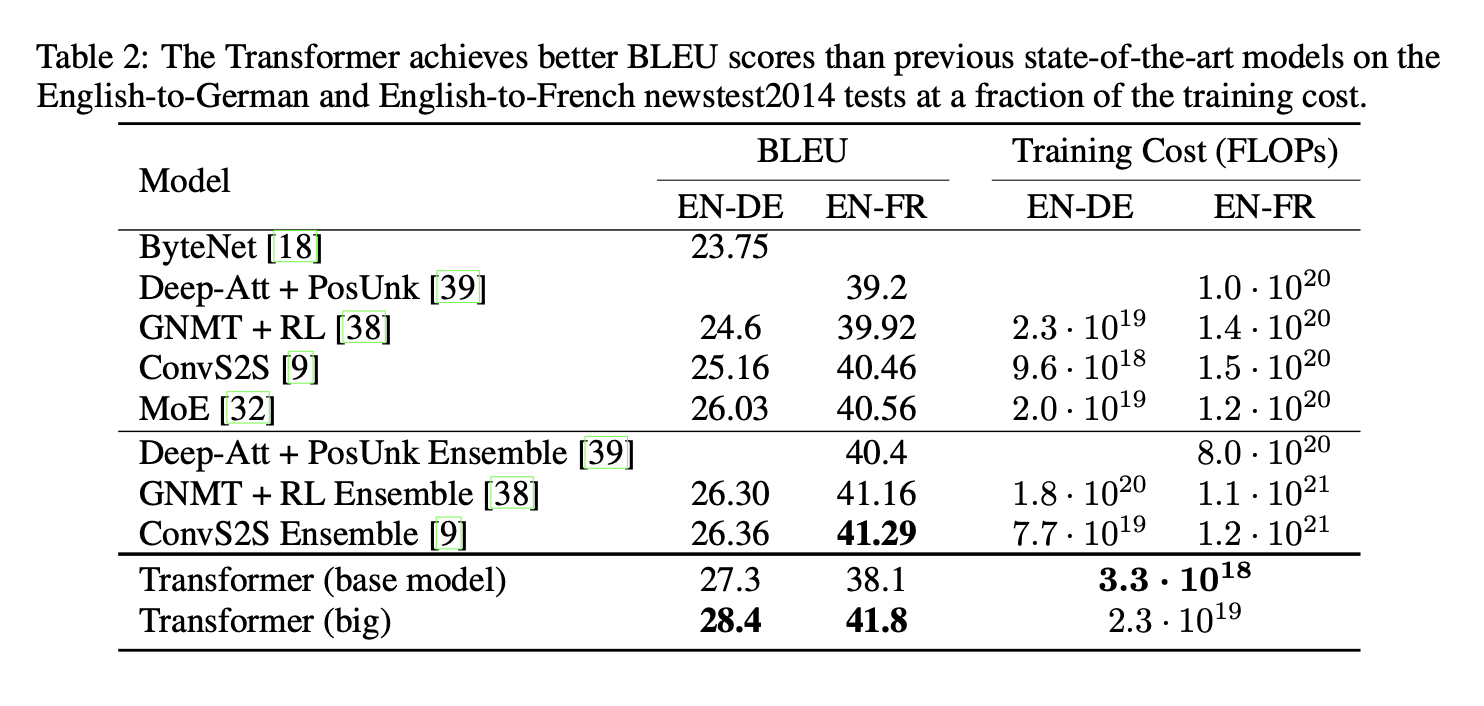
dominant한 sequence transduction model들은 encoder와 decoder를 포함하는 복잡한 RNN 구조을 base로 둔다. Transformer 이전의 SOTA 모델 또한 attention mechanism을 사용한 encoder-decoder 구조를 사용한다. 이 논문에서 제안한 Transformer 모델은 RNN, CNN을 사용하지 않고 attention mechanism만을 기저한 모델이다. 두개의 MT(Machine Translation) task에서 이전의 SOTA 모델들을 ensemble한것과 비교했을때, 훨씬 좋은 BLEU score를 달성했다. Transformer는 parallelizable하기 때문에 학습할 때도 더 적은 시간을 사용한다.

1. Introduction

RNN,LSTM,GRU은 sequence modeling과 (LM, MT task와 관련된) transduction problem에 대해서도 SOTA한 성능을 보였다. Recurrent model들은 input, output sequence의 symbol position에 따라 factor를 계산한다. 각 Time step에 position을 할당하는 computation에서 sequence hidden state, previous hidden state, input을 generate한다. 이것의 본질적인 sequential 특성인 memory limit이 training example간의 batching(일괄처리)을 제한하기 때문에 longer sequence length에서 중요해지는 training에서의 parallelization을 저해한다.

Attention mechanism은 다양한 task에서 sequence modeling, transduction model의 필수부분이 되었고, input 또는 output sequence의 distance와 상관없이 dependencies를 모델링해 줄 수 있다. 하지만 몇몇을 제외하고 대부분은 RNN과 결합하여 사용했다.

이 논문에서는 recurrence를 사용하지 않고, 대신 input과 output 사이의 global dependency를 고려하기 위해 전적으로 attention mechanism만을 사용한다. Transformer는 더 많은 parallelization을 이용할 수 있고, P100 GPU 8개에서 12시간 정도만 학습했음에도 SOTA한 성능을 보였다.

2. Background

sequential computation을 줄이는 목표가 Extended Neural GPU, ByteNet, ConvS2S 모델들을 만드는것에 대해 motivation이 되었다. 이 모델들은 모두 CNN을 basic building block으로 사용한것으로, 전체 Input과 output position에 대해 hidden representation을 parallel하게 계산한다. 이런 모델에서 두 개의 임의의 input 또는 output position의 signal를 relate하는 데 필요한 operation의 수는 position 사이의 거리에 따라 증가한다. Transformer에서 averaging Attention-Weighted positions로 인해 reduced resolution에 대한 cost를 감안하더라도, operation을 O(1)으로 감소 시킨다. Reduced resolution에 대한 cost은 Muli-Head Attention으로 보완하고자 한다.

intra-attention이라고도 불리는 Self-Attention은 sequence의 representation을 계산하기 위해, single sequence에서 different position들을 연관시키는 attention mechanism이다. Self-Attention은 reading comprehension(=Q&A task), abstractive summarization, textual entailment, task-independent sentence representations에서도 성공적으로 사용되고 있다.

End-to-end memory network는 sequence aligned recurrence 대신에 recurrent attention mechanism에 기저하고 있고, simple-language question answering and language modeling tasks에 좋은 성능을 보이고 있다.

Transformer는 sequence-aligned RNN, CNN을 사용하지 않고 전적으로 self-attention에 의존하여 input과 output의 representation을 계산하려는 첫번째 transduction model이다. Transformer, self-attention에 대해 설명하고 그것의 장점에 대해 설명할 것이다.

3. Model Architecture

대부분의 competitive neural sequence transduction Model들은 encoder-decoder structure를 갖고 있다. encoder는 input sequence of symbol representation $(x_1,…,x_n)$ 을 sequence of continuous representation $z=(z_1,…,z_n)$ 으로 맵핑시킨다. 주어진 encoder output $z$에 대해, decoder는 output sequence $(y_1,…,y_m)$of symbol을 하나씩 generate한다. 각 time step에서, 다음 output symbol을 생성할 때, 추가적인 input으로 이전에 generate한 symbol을 사용하기 때문에 auto-regressive하다.

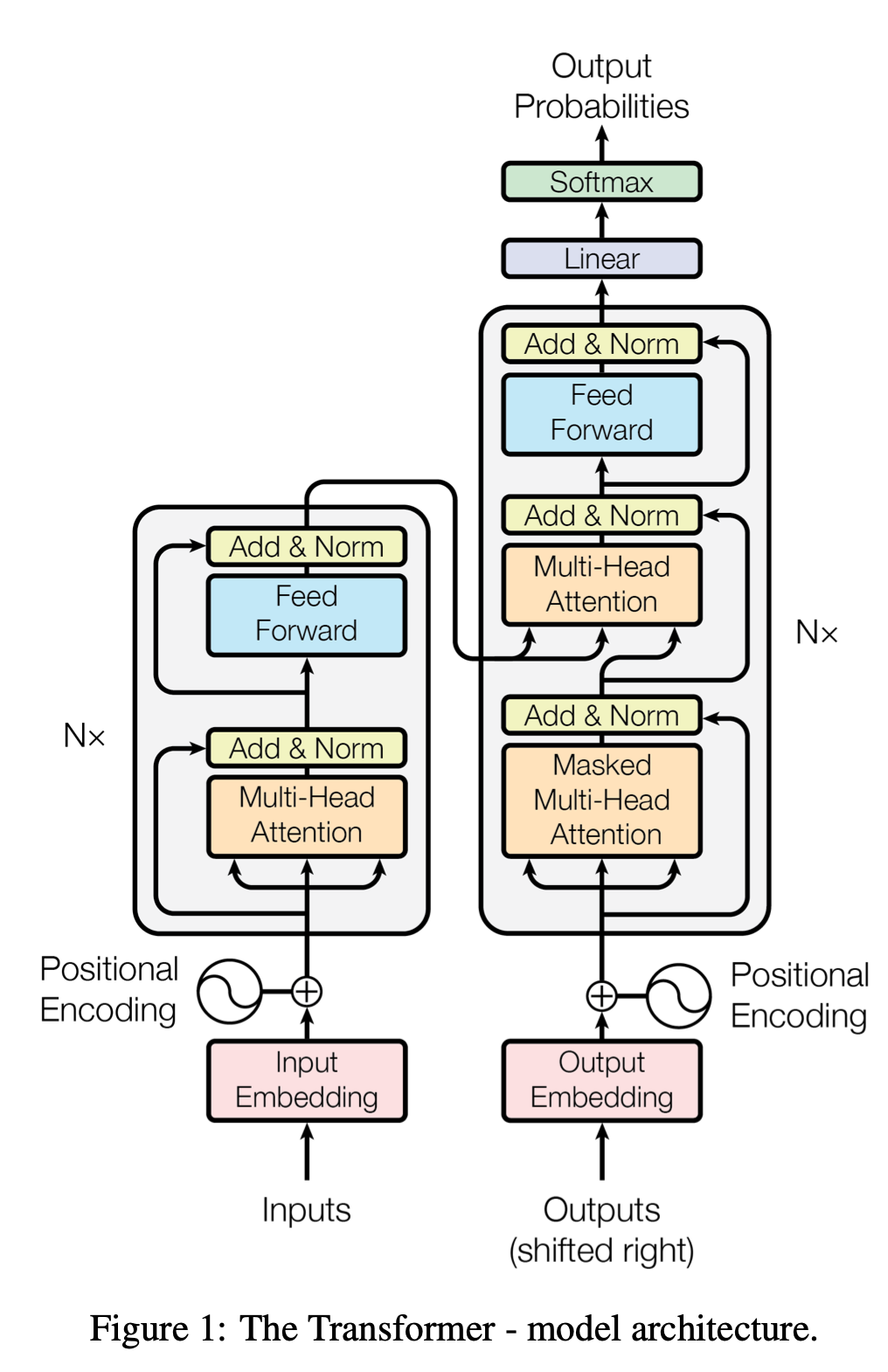
Transformer는 stacked-self-attention과 point-wise (fully connected layers for both encoder, decoder)를 사용하여 방금 언급한 overall architecture를 따른다. 이에 대한 구조가 아래 그림에 나타나 있다.

3.1 Encoder and Decoder Stacks

• Encoder : Encoder는 N = 6 개의 동일한 layer의 stack으로 이루어져 있다. 각 layer는 두개의 sub-layer를 갖는다. 첫번째 sub-layer는 multi-head self-attention mechanism이고, 두번째 sub-layer는 간단한 position-wise fully connected feed-forward network이다. 두개의 sub layer에 각각에 대해 layer normalization이 뒤에 오고, 그 다음 residual connection을 사용되었다.

  각 sub-layer의 output은 $LayerNorm(x+Sublayer(x))$이고, $Sublayer(x)$는 각 sub-layer function의 output이다. 모델의 모든 sub-layer가 Residual connection을 사용하기 위해, $d_{model}=512$ 크기의 dimension을 갖는 embedding layer들을 output으로써 produce한다.

• Decoder : Decoder 또한 N = 6 개의 동일한 layer의 stack으로 이뤄진다. encoder에서 사용했던 두개의 sub-layer를 사용하고, 추가로 decoder는 encoder stack의 output에 대해 multi-head attention을 수행하는 third sub-layer를 사용한다. (위 그림에서 decoder 2번째 sub-layer를 의미한다.) Encoder와 유사하게 각 sub-layer에 residual connection과 layer normalization을 사용한다. 또한 현재 position이 바로 subsequent positions에 attend하는 것을 방지하기 위하여 decoder의 self-attention sub-layer를 수정하였다. 하나의 position에 의해 offset된 output embeddings과 결합된 masking은 position i에 대한 prediction이 i보다 작은 positions에서의 known output에만 depend하게 보장해준다.

  현재 position에서 generate한 output이 아직 generate 되지 않은 output에 attend하면 안되기 때문에 masking을 사용함으로써 이를 해결한다.

3.2 Attention

Attention function은 query와 a set of key-value pair를 output에 맵핑시킨다. 이때, query, key, value, output은 모두 vector이다. Output은 value에 대해 weighted sum으로 계산된다. 각 value에 할당된 weight들은 대응되는 key에 따른 query의 compatibility function에 의해 계산 된다.

3.2.1 Scaled Dot-Product Attention

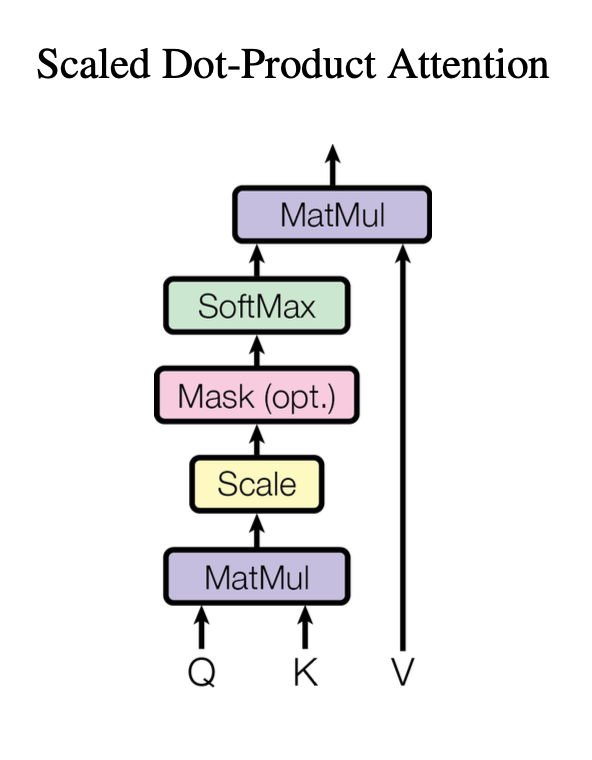
하나의 attention block을 “Scaled Dot-Product Attention”이라 부른다. Input으로는 query, $d_k$ dimension을 갖는 key, $d_v$ dimension을 갖는 value로 이뤄진다. 모든 key와 query의 dot product을 하고, 이것을 $\sqrt{d_k}$로 나눠준 후에 softmax function에 넣어 value들에 대한 weight를 얻는다.

batch size만큼 한번에 계산하기 위해서 실전에선, query 집합을 묶어 matrix Q로 만들어서 attention function을 이용하여 계산한다. key들과 value들 또한 matrix K, V로 만들었고, output matrix를 다음과 같이 계산할 수 있다.

가장 많이 사용되는 두가지 Attention function은 additive attention, dot-product attention이다. Dot-product attention은 scaling factor ${1 \over {\sqrt d_k}}$ 를 제외하고는 본 논문에서 사용한 attention과 동일하다. Additive attention는 single hidden layer로 feed-forward network을 사용하여 compatibility function을 계산한다. 두가지 attention은 theoretical complexity 면에서 유사하지만, dot-product attention이 매우 optimized된 matrix multiplication code로 구현될 수 있기 때문에, 실전에서 훨씬 빠르고 공간 복잡도 면에서도 더 효율적이다.

$d_k$가 작은 값일 때, 위의 두개 mechanism은 유사하게 동작하지만, large value$d_k$로 scaling하지 않을때, additive attention이 dot product attention보다 성능이 더 뛰어나다. Dimension이 큰 Dot product을 softmax function에 push하게 되면 매우 작은 gradient값을 갖게 된다. 그래서 ${1 \over {\sqrt d_k}}$로 dot product attention을 scaling했다.

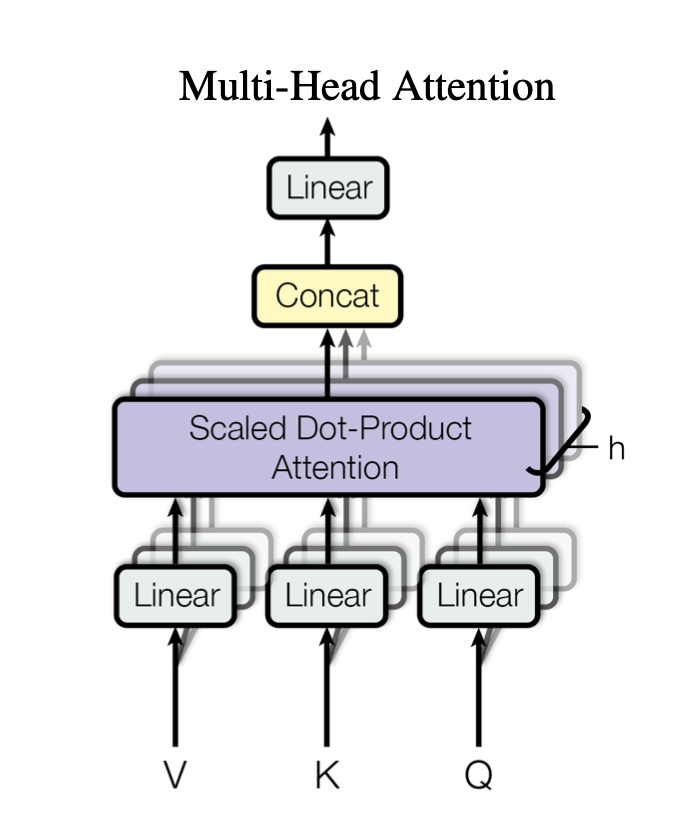
3.2.2 Multi-Head Attention

$d_{model}$-dimensional keys, values, queries에 대해 한번 attention function을 연산하는 것 보다 $d_k,d_k,d_v$ dimension에 대해 학습된 linear projection을 h번 사용하여 keys, valeus, queries을 linearly project하는 것이 더 beneficial하다. 각 query, key, value들에 대해 각각의 projected version에 대해서, parallel하게 attention function을 수행하여 $d_v$ dimension을 갖는 output을 계산했다. 위의 그림처럼 이 값들은 concatenate되어 한번 project되어 final value를 계산하게 된다.

Multi-head attention은 model이 different position의 different representation subspace에서 information들을 jointly attend하게 해준다.

projection의 parameter값들은 다음과 같다.

$W_i^Q \in R^{d_{model}×d_k}$, $W_i^k\in R^{d_{model}×d_k}$$W_i^V\in R^{d_{model}×d_v}$,$W^O\in R^{hd_{v}×d_{model}}$ e

본 논문에서 h = 8 parallel attention layers(or heads)를 사용했다. $d_k=d_v=d_{model}/h=64$의 값을 사용하였다. 각 head의 reduced dimension 때문에, total computational cost는 full dimensionality를 갖는 single-head attention과 유사하다.

3.2.3 Applications of Attention in our Model

Transformer는 multi-head attention을 세가지 다른 방식으로 사용한다.

• encoder-decoder attention layer에서, previous decoder layer에서 나온 query를 가져오고, encoder의 output에서 memory keys와 values 가져온다. 이것들은 decoder의 모든 position에서 input sequence의 모든 position에 attend하게 해준다. sequence-to-sequence model에서의 encoder - decoder attention mechanism을 모방한다.
• Encoder는 self-attention layer를 포함한다. Self-attention에서 모든 key, value, query들은 모두 encoder의 previous layer의 output에서 가져온다. Encoder에서의 각 position은 encoder의 previous layer의 모든 position에 attend 할 수 있다.
• 유사하게, decoder에서의 self-attention layer들은 decoder의 각 position이 현재 position까지의 모든 position에 대해 attend 할 수 있게한다. Auto-regressive property를 preserve하기 위해 decoder에서의 leftward information flow를 prevent할 필요가 있다. 우리는 illegal connection에 해당하는 softmax 입력의 모든 값을 마스킹(-∞로 설정)하는 것을 scaled dot-product Attention의 내부를 구현했다.

3.3 Position-wise Feed-Forward Networks

attention sub-layer 외에도, encoder, decoder의 각 layer는 각 위치에 개별적으로 동일하게 적용되는 fully connected feed-forward network를 포함한다. ReLU activation function을 사용한 두개의 linear transformation으로 이뤄져있다.

Different position에 대해선 같은 linear transformation을 사용하는 반면, layer들에 대해선 다른 parameter들을 사용한다. input과 output의 dimensionality는 $d_{model}=512$이고, inner layer의 dimensionality는 $d_{ff}=2048$이다.

3.4 Embeddings and Softmax

다른 sequence transduction model들과 유사하게, Input token들과 output token들을 vector dimension $d_{model}$로 바꾸기 위해 learned embedding을 사용한다. 또한 decoder output을 predicted next-token probabilities로 바꾸기 위해 usual learned linear transformation과 softmax function을 사용한다. Model에서, 같은 weight matrix를 two embedding layers와 pre-softmax linear transformation 사이에 공유한다. embedding layer에서는 이 weight들에 대해 $\sqrt{d_{model}}$을 곱해준다.

3.5 Positional Encoding

우리의 model들이 recurrence, convolution이 없기 때문에, 모델이 sequence의 순서를 활용하기 위해, sequence에서의 token의 relative or absolute position에 대한 정보를 추가해줘야 한다. 이를 위해 “positional encoding”을encoder stack , decoder stack의 bottom에 위치한 input embedding에 추가한다. positional encoding은 embedding과 동일한 dimension을 갖는 $d_{model}$을 갖고 있어서 두개를 합칠 수 있다. positional encoding에 대해서 학습하고 fixed하는 것에 대해 많은 방법이 있다.

positional encoding에 대해 different frequency를 갖는 sine, cosine function을 사용했다.

$pos$는 position을 $i$는 dimension을 의미한다. positional encoding의 각 dimension은 sinusoid에 대응된다. wavelength는 $2\pi$ 부터 $10000*2\pi$의 범위의 geometric progression을 형성한다. 어떠한 fixed offset $k$에 대해, $PE_{pos+k}$는 linear function of $PE_{pos}$로 나타낼 수 있어서, relative position에 의해 attend하는 법을 모델이 쉽게 학습된다고 가정을 했기 때문에 이 함수를 선택했다.

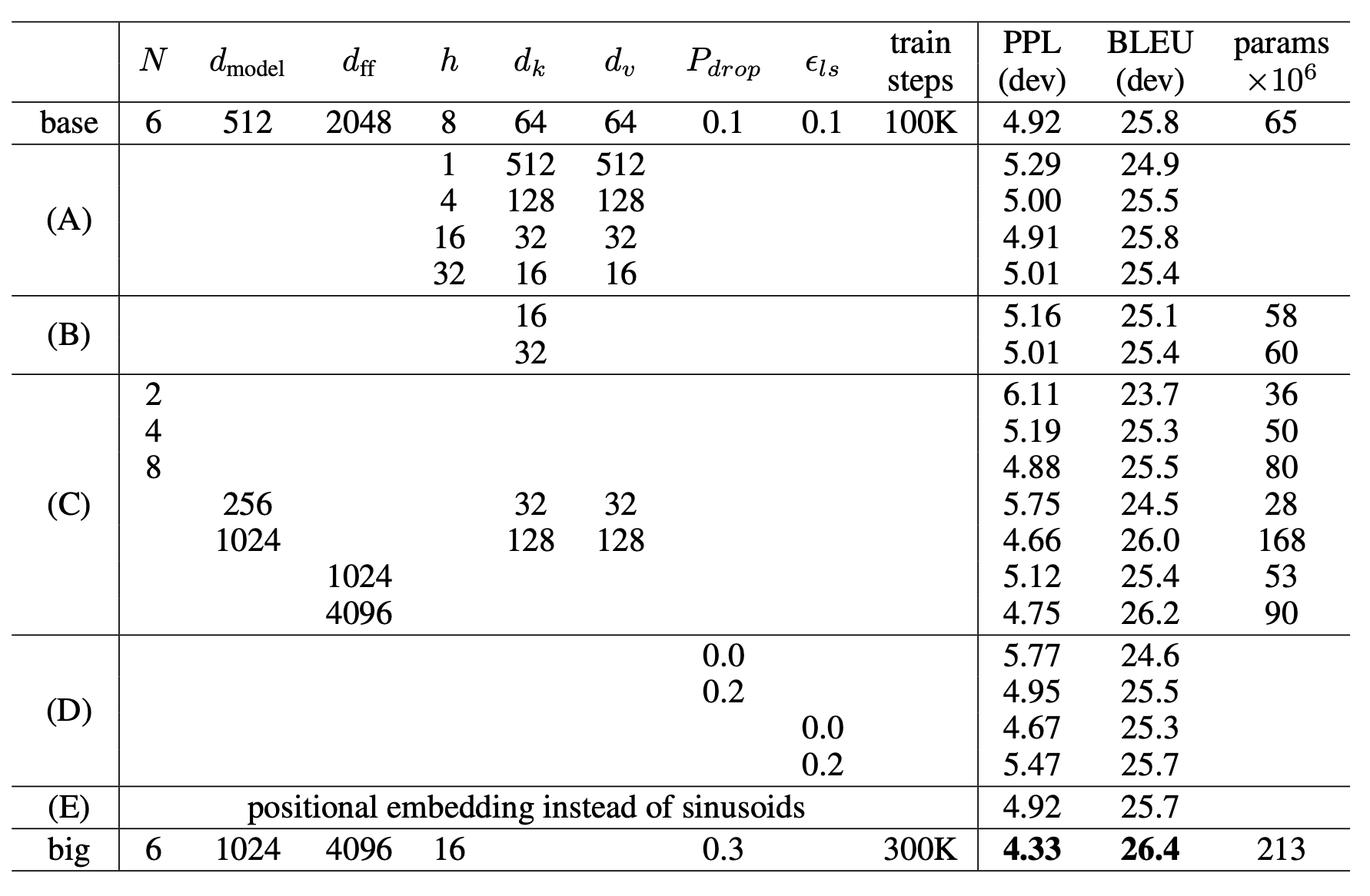
learned positional embedding을 사용하여 실험하는 대신, 위의 table row E에서 볼 수 있듯이 두개의 버전이 거의 동일한 결과를 내는 것을 발견했다. sinusoidal version을 선택했고, 왜냐하면 모델잉 학습하는 동안 만난 trained dataset보다 더 긴 sequence를 추론 가능하게 하기 때문이다.

4. Why Self Attention

이 section에서는 self-attention layer과 RNN,CNN layer들을 다양한 측면에서비교할 것이다. self-attention의 사용에 대한 근거로 세개를 들었다.

1. layer마다의 total computational complexity
2. 최소하느이 sequential operation들이 요구되는 연산에 대해 parallelized되는 computation의 양.
3. network에서의 long-range dependency사이의 path length이다. 많은 transduction task에서 long range dependency를 학습하는 것은 key challenge이다. 이러한 dependency를 학습하기 위한 ability에 영향을 끼치는 key factor 중 하나는 network에서 forward, backward 신호가 traverse해야 하는 path 길이이다. input, output sequence에서 어떠한 position combination사이의 짧은 path는 더 긴 범위의 dependency를 학습하기 쉽다. 그래서 different layer type들로 이루어져 있는 network에서 any input, output position에 대해서 Maximum path length를 비교했다.

Table 1에서 볼 수 있듯이, self-attention layer는 모든 position에 대해 O(1)의 sequential하게 실행되는 operation을 수행하는 반면, recurrent layer는 O(n) sequential operation을 필요로 한다. computational complexity면에서 sequence length n이 representation dimensionality d 보다 작을때, self-attention layer들은 recurrent layer들보다 훨씬 빠르다. word-peice, byte-pair representation과 같은 sentence representations을 사용하는 대부분의 MT task의 SOTA model에서 $l<d$이 성립한다.

long dependency를 포함한 task에서 computational performance를 향상시키기 위해, self-attention은 각각의 output position을 중심으로 한 input sequence에서 크기 r의 이웃만을 고려하는 것으로 제한되었다. 이것은 maximum path length를 $O(n/r)$으로 증가시킬 수 있다.

k<n인 single convolution layer만 있는 kernel은 all pair of input과 output position을 연결하지 않는다. 그래서 O($log_k(n)$의 dilated convolutions 혹은 O(n/k)의 contiguous kernels와 같은 경우, $O(n/k)$ convolution layers을 쌓는 것을 요구한다. (network에서의 2개의 position에 대해 longest path의 length를 증가시키기 위해) 보통 CNN이 RNN보다 k배 만큼 연산이 expensive하다. 하지만 Separable convolution에 대해선 complexity가 $O(k\cdot n \cdot d +n\cdot d^2)$로 매우 감소한다. 하지만 $k=n$인 경우, Complexity off separable convolution과 우리 model에서 사용한 self-attention layer는 동일하다.

추가적으로, self-attention은 더 interpretable한 Model을 제공한다. attention distribution에 대해 appendix에서 다뤘다. 각각의 attention head가 different task를 학습할 뿐만 아니라, sentence의 syntactic & semantic structure와 관련된 behavior를 보여준다.

5. Trainig

5.1 Training Data and Batching

• standard WMT 2014 English-German dataset consisting of about 4.5 million sentence pair
• Sentences were encoded using byte-pair encoding which has a shared source- target vocabulary of about 37000 tokens
• larger WMT 2014 English-French dataset consisting of 36M sentences and split tokens into a 32000 word-piece vocabulary [38]. Sentence pairs were batched together by approximate sequence length
• Each training batch contained a set of sentence pairs containing approximately 25000 source tokens and 25000 target tokens.

5.2 Hardware and Schedule

• 8 NVIDIA P100 GPUs.
• hyperparameters는 table에 명시.
• he base models for a total of 100,000 steps or 12 hours. each training step은 0.4sec.
• big models에 대해선 each step 1.0 sec, 300,000 steps (3.5 days).

5.3 Optimizer

• Adam optimizer [20] with β1 = 0.9, β2 = 0.98 and ε = 10−9

• learning rate는 다음과 같다.

  

  first warm_up steps까지 lr을 linear하게 증가시키다가, 위의 수식 처럼 감소시켰다. warmup_steps = 4000.

5.4 Regularization

Three types of regularization during training

1. Residual Dropout
   1. dropout [33] to the output of each sub-layer, before it is added to the sub-layer input and normalized.
   2. dropout to the sums of the embeddings and the positional encodings in both the encoder and decoder stacks
   3. base model에 $P_{drop}=0.1$을 사용했다.
2. Label Smoothing
   1. label smoothing of value $\epsilon$ = 0.1 [36]. This hurts perplexity, as the model learns to be more unsure, but improves accuracy and BLEU score.

6. Results

6.1 Machine Translation

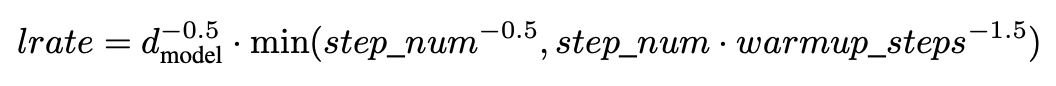
6.2 Model Variations

6.3 English Constituency Parsing