CS224N|Lecture 7 Vanishing Gradients, Fancy RNNs
18 Nov 2021
RNN의 vanishing/exploding gradient problem이 왜 생기고, 왜 문제가 되는지 에 대한 내용, 그에 대한 (완벽하지 않지만) 해결책인 LSTM과 그 구조의 원리에 대한 내용, 그리고 Bidirenctional LSTM에 대해서 배웠습니다.

RNN의 문제점인 Vanishing gradient problem을 먼저 살피고, 그에 대한 해결책인 LSTM,GRU를 살펴본다.
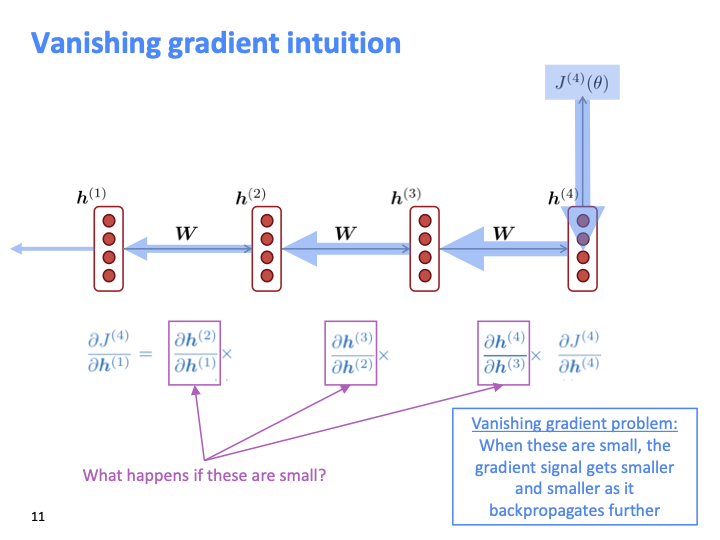
back propagate할때, 이 gradient들이 매우 작다면 gradient의 곱이 0에 수렴할 것이다. 그러면 아무것도 업데이트하지 못하게 된다.
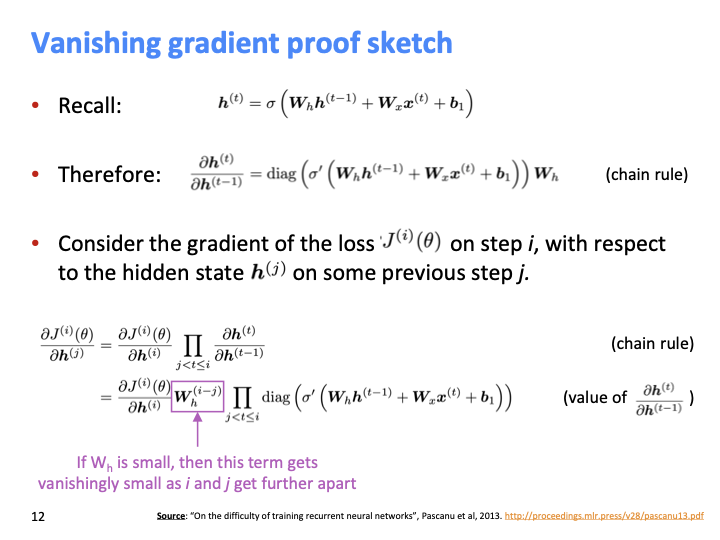
vanila RNN에 대한 식이 위와 같이 주어졌다.
$W_h$ 매우 작다면, $(i-j)$값만큼 $W_h$가 exponential하게 작아진다. 이것이 큰 문제인 vanishing gradient 문제이다.

W의 가장 큰 eigenvalue가 1보다 작다면 gradient는 shrink된다.
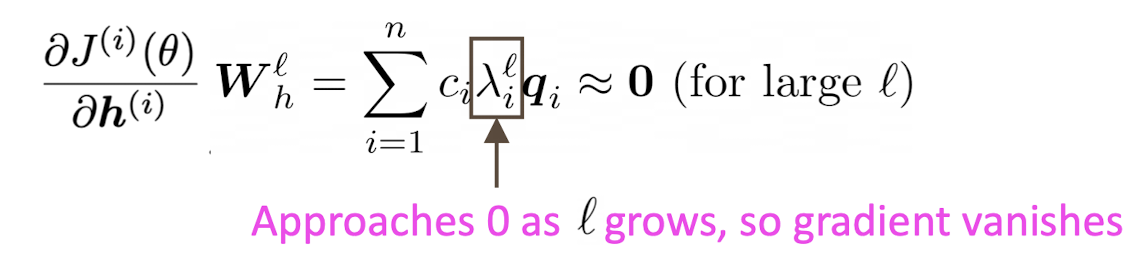
$q_i$ : eigenvector를 의미한다.
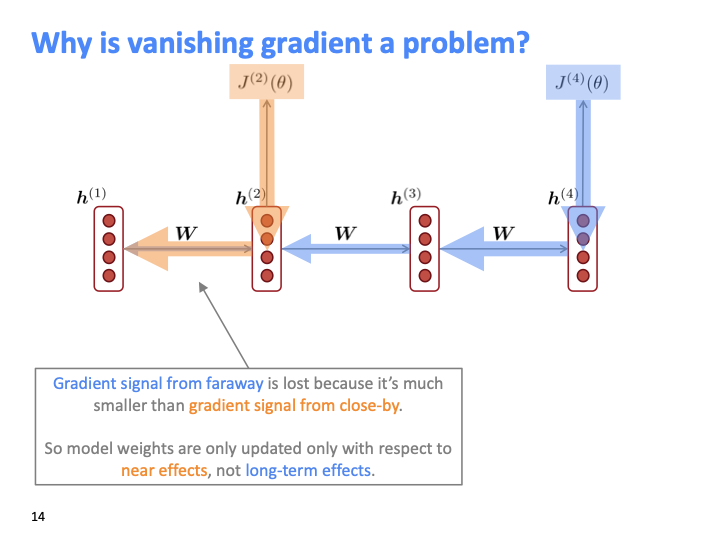
gradient signal은 가까이 있는 것이 멀리서 오는 것보다 더 크다. 즉, near effect에 대해서만 optimize되고, long term effect는 반영되지 않는다.

Vanishing gradient가 문제가 되는 이유는 다음과 같다.
- step t와 step t+n에 대해 아무 dependecy 없이 학습 될 수 있다.
- dependency가 있다고 해도, wrong parameter가 있어서, true depency를 게산할 수 없다.

주어진 문장이 매우 길고, predict하려는 단어는 마지막 빈칸에 들어갈 단어이다. RNN LM이 쉽게 이 질문에 답할 수 있을까? grdient이 매우 작다면 dependency을 학습할 수 없다. 즉, RNN LM은 long distance dependecies를 예측하지 못한다.

syntactic recency는 다음 단어를 올바르게 예측하기 위해서는 syntactically close한 단어를 골라야한다. dependency path로 구성된 tree를 보면 writer가 가장 short path이기 때문에 is가 와야 한다.
반면 sequential recency는 문장에서 단어들이 얼마나 가까운지에 대한 것이다. books가 더 가깝기 때문에 are이 오게 된다.
Vanishing gradient 때문에 RNN-LM은 후자인 sequential receny를 통해 학습하고, 더 많은 에러를 만들게 된다.

gradient 값이 매우 커지면 SGD가 업데이트 되는 값 또한 매우 커진다. 그러면 매우 big step으로 model을 drastically하게 변화시킨다. 이것이 exploding gradient이다.

exploding gradient 해결책은 gradient clipping이라는 것인데, norm of gradient가 threshold보다 크면 SGD 를 적용하기 전에 scale down하는 것이다.

위의 그래프에서, x,y축은 parameter이고 z축은 loss를 의미한다. 왼쪽 그림을 보면 그림이 overshoot된것을 볼 수 있고, very steep gradient가 있어서 big step으로 학습된것이다. 오른쪽 그림의 경우, gradient clipping이 존재하여 less dramatic하게 학습되고, 안전하게 update 한다고 볼 수 있다.

RNN이 많은 timestep에 대해 정보를 보존하면서 학습하는 것은 매우 어렵다. hidden state은 계속해서 rewritten된다. 그에 대한 해결책으로 RNN with separate memory로, LSTM에 대한 아이디어라고 할수 있다.

LSTM은 cell에 erase, write, read하면서 정보를 유지한다. 특정 정보가 erase/write/read 될지는 그에 따른 세개의 gate에 의해 결정된다. 각 time step마다 각 gate는 open(1) 되거나 closed(0)된다. open : 어떤 정보가 pass through 되는것을 의미하고, closed = not pass through를 의미한다.
여기서 중요한 것은 gate들은 dynamic하다는 것이다. 전체 sequence에 대해 constant value가 아니다. dynamic이 의미하는 것은 각 timestep마다 다르다는 것을 뜻한다.

파란색 박스를 보면 three gate들을 어떻게 쓰는지 알 수 있다. $f^{(t)},i^{(t)},o^{(t)}$식을 보면 이전 hidden state output과 현재 timestep의 입력이 들어가기 때문에 dynamic한 값인것을 볼 수 있다.
마지막 $c^{(t)}$식의 $f^{(t)}$(forget gate)에 대해서 설명하겠다. $f^{(t)}$는 0과 1로 이루어진 vector이고, $c^{(t-1)}$와 element wise 하는 것은 masking outg하는 것과 동일하다고 볼 수 있다. ($c^{(t)}$ : cell value)
LSTM의 hidden state를 RNN의 output처럼 생각할 수 있다. cell은 internal memory이지만, 다음 단계의 hidden state로 전달 된다.
학생의 질문 중에, 위의 $f^{(t)}$의 식에 $h^{(t-1)}$만 있고, $c^{(t-1)}$에 대한 식은 없는지 물어본 질문이 있었다. 그에 대한 답변은 (확실하진 않다고 했다) $h^{(t-1)}$가 $c^{(t-1)}$의 정보를 대부분 포함한다고 했다.
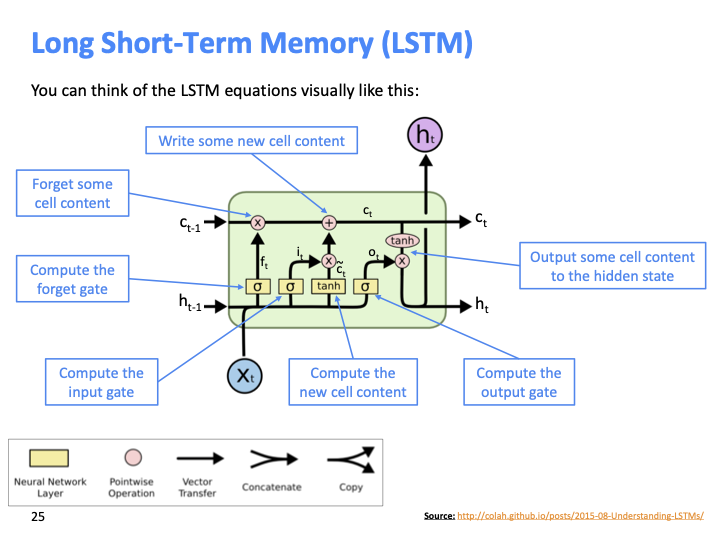
LSTM구조를 도식화한 diagram이다.

LSTM이 어떻게 vanshing gradient를 해결하는지에 대한 답변이다. LSTM 구조가 더 많은 step들에 대해 정보를 보존하기가 RNN보다 더 좋은 구조이지만, vansihing/exploding gradient 문제가 일어나지 않는다고 보장할 순 없다. 위에서 예를 든것과 같이 forget gate가 모두 1로 설정 (remember every thing) 이라면, cell에 어떤 정보가 저장될지는 불명확해진다.
왜 더 좋은 구조인지에 대한 설명은 다음과 같다. vanila RNN에서는 hidden state가 bottle neck처럼 작동해서, 모든 gradient들이 must pass through해야 했다. 그래서 hidden state의 gradient가 작다면 down stream의 gradient값들 또한 작아지게 된다. 반면 여기 cell들은 short cut connection 처럼 작동하고, forget gate =1이라면 cell stay same일것이고 그로인해 vanishing problem이 일어나지 않을것이다. 다시 말하면 vanishing gradient 문제가 일어나지 않을 rotue가 존재한다고 볼 수 있다.

LSTM은 2015년까지 dominant한 구조였고, 2021년도에서는 Transformer 구조가 dominant하다. 이후 수업에서 Transformer에 대해 다룰 예정이다.
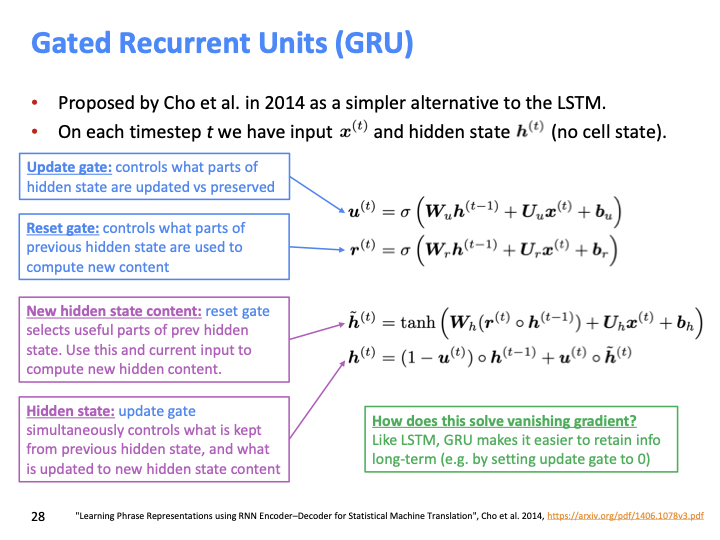
LSTM의 unnecessary한 complexity를 제거하기 위해 GRU가 나왔고, GRU에는 cell state가 없다. LSTM과 GRU가 공통 된것은 flow of info에 대해 gate를 이용하여 control한다는 것이다.
update gate = forget gate in LSTM, Reset gate = select previous hidden state which part is useful. update gate는 previous hidden state와 새로운 입력에 대해 balance을 set한다고 볼수있다. 만약에 $u^{(t)}$ 값이 0이라면, hidden state를 유지하는 것을 의미하고, 이것이 vanishing problem을 해결하는 방법이라고 할 수 있다.
$(1-u^{(t)})$ 와 $u^{(t)}$ 가 LSTM에서는 별도의 gate로 존재한다.

GRU가 LSTM보다 더 간단하고 빠르고, 더 적은 파라미터수를 갖는 모델이지만, 보통 LSTM의 성능이 좋다. 그래서 LSTM으로 시작하고 먄약 더 효율적인 것을 원한다면 GRU를 사용해라.
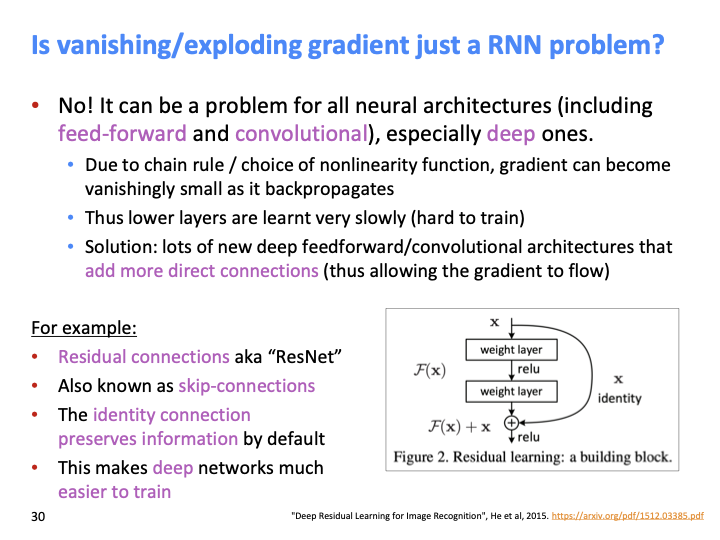
vanishing/exploding grdient problem은 RNN의 문제만은 아니다. (convolution, feed-forward에서도 일어난다.) 낮은 layer의 gradient값은 높은 layer의 gradient보다 훨씬 작기 때문에 SGD 동안 배우 느리게 계산된다. 그래서 해결책은 더 많은 direct connection을 추가하는 것이다. 대표적인 방법인 ResNet이다. 또 다른 방법으로는 Dense connection을 사용하는 DenseNet, HighwayNet 등이 있다.
결론은 RNN은 같은 weight matrix를 반복하여 곱하는 것 때문에 vanishing/exploding gradient 문제가 발생하여 unstable하다는 것이다.
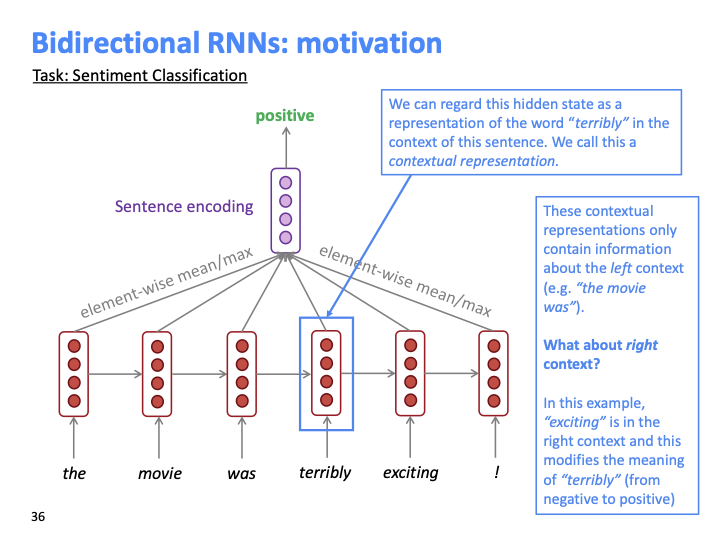
다음 문장 “the movie was terribly exciting!”에 대해 “terribly”라는 단어를 중심으로 보자. terribly까지의 context가 학습된 저 hidden state를 contextual representation이라고 할 수 있고, 이 표현은 오직 왼쪽 context만을 근거하여 학습한다. terribly 자체는 부정적 의미지만 exciting이 붙여져서 긍정적 의미가 되었다.
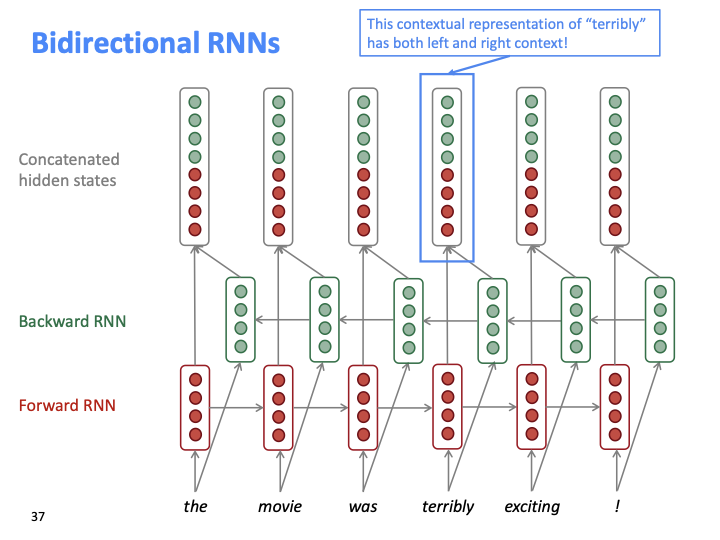
만약 위와 같이 backward RNN을 추가해주면, left, right context 모두에 대한 표현이 학습된다.

다음은 BiRNN에 대한 간단한 수식이다.

Bidirectional RNN은 전체 입력 sequence에 대해 접근 가능할 때만 사용할 수 있다. 그래서 왼쪽 context에 대해서만 접근 가능한 LM task에는 적합하지 않다. SOTA 모델은 BERT 또한 양방향으로 build 되었다.

multiple RNN을 사용하여 deep 하게 학습시키는 방법을 Multi-layer RNN이라고 하고, stacked RNN이라고도 한다.

2017년 구글에서 나온 논문에서는 2~4 layer의 RNN이 MT task에 적합하다고 하였다. RNN은 다른 종류의 network 처럼 deep 하게 학습될 수 없다. RNN은 sequential하게 학습되고, parallel하게 학습되지는 않는다. 그래서 계산하는것이 비싼 비용을 요구한다. (하지만 skep-conneciton을 이용한 RNN은 deep하게 학습되어야 한다.)
Transformer-based network은 최대 24 layer로 학습될수 있을만큼 deep하게 학습된다. (Transformer은 skip connection같은 것이 많이 있다고 할수 있다.)