위상정렬(Topological sort)
14 Aug 2021
CTP 알고리즘 동아리에서 여름방학 코딩테스트반에 참여하여 공부한 내용입니다.
아래 자료는 수업에서 사용한 내용입니다.
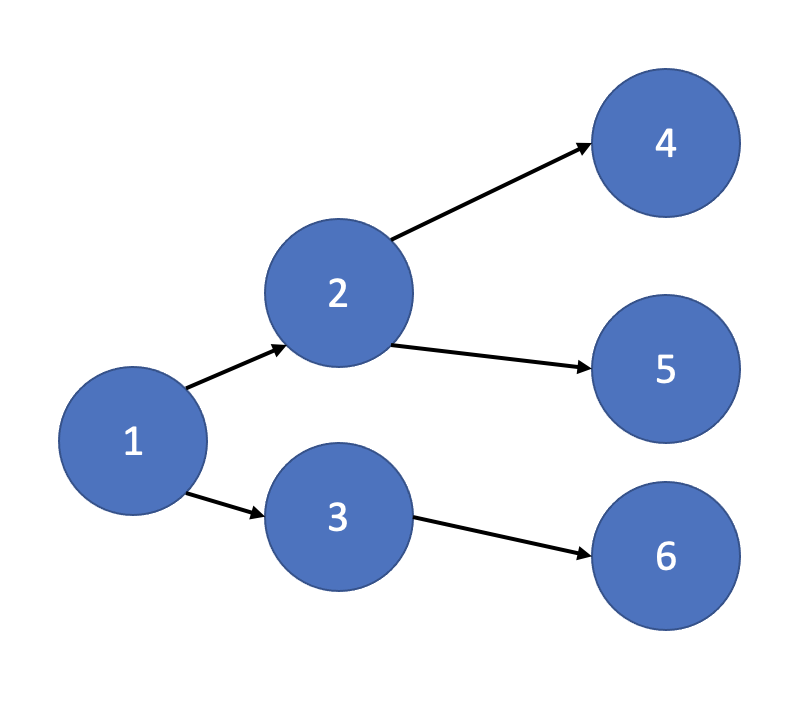
DAG에서 위상에 따라 방향성을 거스르지 않게 나열하는 알고리즘을 위상정렬(topological sort)이라고 합니다. 예를들어 아래 그림에서 위상에 따라 출력해보면, 1,2,4,5,3,6 입니다. (답이 여러개일 수 있습니다.)
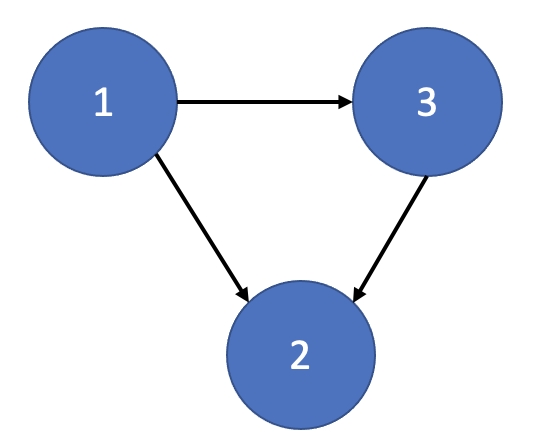
DAG (Directed Acyclic Graph)는 개별 요소들이 순환하지 않는 비순환 방향 그래프를 뜻합니다. 가령 아래와 같은 그래프 또한 비순환이므로, DAG에 속합니다.
모든 그래프 dp문제에서 그래프는 DAG입니다.만약 사이클이 있다면 memorization이 순환적으로 의존하게 되므로 문제가 생깁니다. 그리고 위상정렬이 가능하다는 말은 그래프가 DAG라는 말과 동치입니다.
위상정렬의 구현에는 크게 dfs, bfs로 구현하는 두가지 방법이 있습니다. 각 구현의 차이점은 dfs에서는 out-degree가 0인것 부터 정렬하고 , bfs에서는 in-degree가 0인것 부터 정렬하는 차이점이 있습니다.
DFS로 DAG 구현
void dfs(int x){
visit[x]=true;
for(auto i:v[x]){
if (!vis[i]) dfs(i);
else if (!finish[there])
cycle = 1;
}
finish[here] = true;
st.push_back(x);
}
위와 같이 간단하게 구현할 수 있습니다. dfs를 실행시키면 dfs가 끝나는 순서대로 역순으로 위상이 정렬됩니다. 어떤 정점에서 dfs가 끝나면 스택에 하나씩 삽입해주면 됩니다.쉽게 말하면 나가는 간선이 없는 정점부터 스택에 push하여 정렬하는 것 입니다.
dfs로 cycle의 유무를 아는 방법 다음과 같습니다. 나가는 간선이 없는 정점들에 대해서 표시를 해두고, 만약 그 간선이 다시 호출되었다면, 역방향으로의 간선이 있으므로 사이클이 있다는것을 알 수 있습니다.
BFS로 DAG 구현
vector<int> topological_sort() {
queue<int> q;
for (int i = 1; i <= n; ++i) {
if (!indeg[i]) q.push(i);
}
vector<int> tp_order;
while (q.size()) {
int u = q.front(); q.pop();
tp_order.push_back(u);
for (int v : g[u]) {
// u가 사라지면 v의 진입차수가 감소
// 진입차수가 0이라면 위상이 가장 높으므로 큐에 넣음
if (!--indeg[v]) {
q.push(v);
}
}
}
// 사이클 감지 // 정렬이 끝까지 안 됐다면 빈 벡터 반환
if (tp_order.size() < n) return vector<int>();
return tp_order;
}
bfs로 구현하기 전에 각 정점에 대해 들어오는 간선의 수를 세줍니다. 그리고 들어오는 간선이 없는 정점들을 큐에 삽입한 후, bfs를 합니다. 탐색 할때, 방문한 정점에 대해 들어오는 간선의 수를 하나씩 감소시킵니다. 들어오는 간선의 수가 0이라면 위상이 가장 높으므로 큐에 넣고 진행합니다.
bfs로 구현했을때, cycle이 있다면, 정렬할때 만든 스택의 크기가 총 노드의 수보다 작습니다.
A - 줄 세우기
간단한 위상정렬 문제입니다.문제에서 DAG라고 주어지지는 않았지만, 예를들어 세명의 학생이 있다고 해보자. 첫번째 학생의 키>두번째 학생의 키, 두번째 학생의키 > 세번째 학생의 키라고 했을때, 세번째 학생의 키> 첫번째 학생의 키는 불가능 하므로 DAG인것을 알 수 있습니다.
스폐셜 저지 문제를 처음 풀어봤는데, 답이 여러개가 가능한 경우 스폐셜 저지 문제라고 합니다. (같은 위상인 경우 순서가 없기 때문) dfs로 구현하여 풀었습니다. 시간복잡도는 O(E+V) 입니다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <tuple>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
using tup = tuple<int,int,int>;
typedef long long ll;
typedef pair<int,int> pi;
int n,m;
bool visit[32001];
vector<vector<int>> v;
vector<int>st;
void dfs(int x){
visit[x]=true;
for(auto i:v[x]){
if(!visit[i]) dfs(i);
}
st.push_back(x);
}
int main(){
cin>>n>>m;
v.resize(n+1);
for(int i=0,p1,p2;i<m;i++){
cin>>p1>>p2;
v[p1].push_back(p2);
}
for(int i=1;i<=n;i++){
if(!visit[i])dfs(i);
}
while(!st.empty()){
cout<<st.back()<<" ";
st.pop_back();
}
return 0;
}
B - ACM Craft
문제를 읽어보면 그래프가 사이클이 없는 DAG인 것을 알수 있습니다. dfs와 dp를 이용하여 문제를 풀었고, 시간복잡도는 O(E+V) 입니다.
방문할 후행 노드의 시간 = max(선행노드가 완료될 시간+후행노드의 시간, 후행 노드의 시간)으로 구현이 가능합니다.
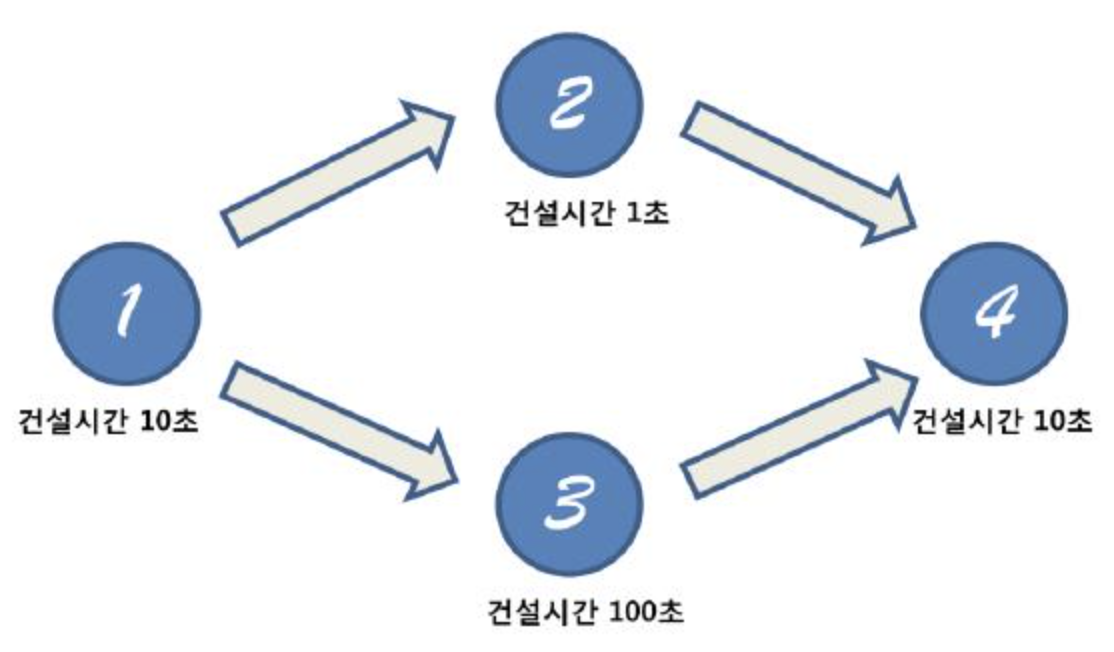
예를들어, 문제에서 주어진 예시인 위 그림에서 1→2→4, 1→3→4 순으로 탐색된다고 해보자. 1→2→4에서 d[4] = 21초가 저장되고, 1→3→4에서 120>21이므로 120이 저장됩니다.
방문하면서 각 정점마다 들어오는 간선의 수(in-degree)를 감소시켜, 0이 아닐 경우에만 dfs를 호출했습니다. 0인 경우, 더 이상 해당 노드의 후행노드 값들에 대해 업데이트하지 않아도 되기 때문입니다.
또한. 어떤 정점에서 시작할지 정해져 있지 않기 때문에, in-degree가 0인 정점들을 큐에 push해주고 큐의 각 정점에 대해 탐색했습니다. 승리하기 위해 건설해야할 건물 번호에 대해 탐색이 되었을 때, 표시를 하여 답을 출력했습니다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <queue>
#include <tuple>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
using tup = tuple<int,int,int>;
typedef long long ll;
typedef pair<int,int> pi;
vector<vector<int>> v;
int t,n,k,w;
int indg[1001];
bool visit[1001];
int d[1001];
int T[1001];
bool check = false;
void dfs(int x){
if(x==w)
check=true;
if(d[x]==-1)
d[x] = T[x];
visit[x]=true;
for(auto k:v[x]){
d[k]=max(d[x]+T[k],d[k]);
--indg[k];
if(!indg[k]) dfs(k);
}
}
int main(){
cin>>t;
while(t--){
cin>>n>>k;
memset(indg,0,sizeof(indg));
memset(d,-1,sizeof(d));
memset(visit,false,sizeof(visit));
v.clear();
v.resize(n+1);
for(int i=1;i<=n;i++)cin>>T[i];
for(int i=1;i<=k;i++){
int p1,p2;
cin>>p1>>p2;
v[p1].push_back(p2);
indg[p2]+=1;
}
cin>>w;
queue<int>q;
for(int i=1;i<=n;i++){
if(!indg[i]) {
q.push(i);
}
}
while(!q.empty()){
int cur = q.front();
q.pop();
dfs(cur);
if(check)
{
cout<<d[w]<<endl;
check=false;
break;
}
}
}
}
C - 동굴 탐험 [카카오 인턴]
풀고나서 업로드하겠습니다.