CS224N|Lecture 3 Word Window Classification, Neural Networks, Matrix Calculus
07 Aug 2021
Neural network이 어떻게 작동하고, back propagation을 통해 parameter들이 어떻게 update되는지에 대한 내용이었다. 또 NER(Named Entity Recognition)문제가 어려운 이유와 간단한 해결 방법에 대해 설명했다. 기본적인 Neural network에 대한 슬라이드의 설명은 생략하겠다.

학생의 질문 중 하나였다. 위의 cross entropy식에서 p(c)에 해당하는 것이 ground truth에대한 probability distribution인데, 이 값에 대해 모르는 값과 true라고 알고있는 값이 섞여 있는 경우에 대해서는 어떻게 해야하는가를 물어봤다. 교수의 답은 현실에 많이 있는 경우이고, semi-supervised learing과 같은 분야의 연구주제라고 하였다. 모르는 label에 대해 확률을 추정하여 p를 결정한다고 하였다.
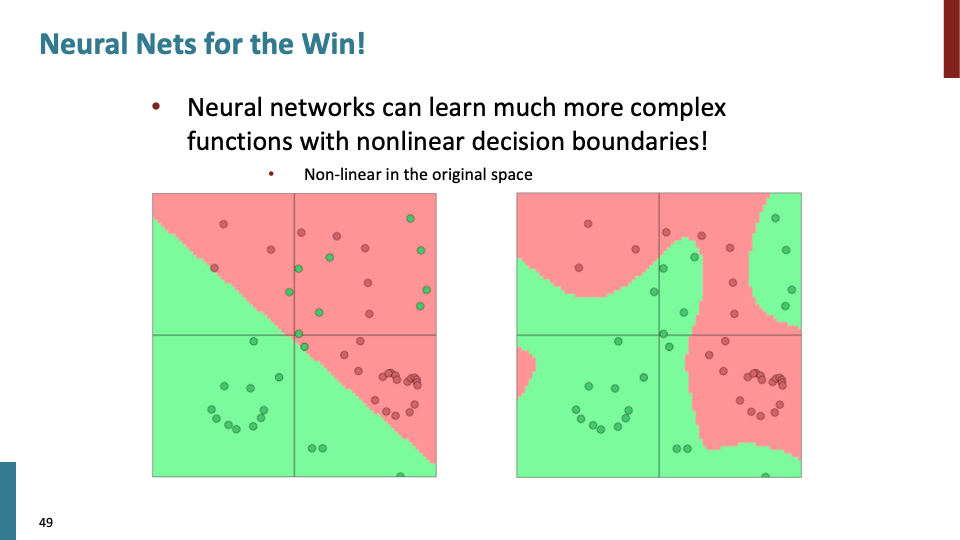
Neural network은 복잡한 function들로 non-linear decision boundaries를 학습할 수 있다.
이번 수업에서 Neural Net for NLP에 대해 언급할 내용은 2가지인데, 하나는 word vector에 관한것, 두번째로는 deeper multi-layer network에 관한것이다.

word vector에서의 Neural Net : parameter들이 w(weight) 뿐 만아니라, word representation 자체 또한 model의 parameter이다.
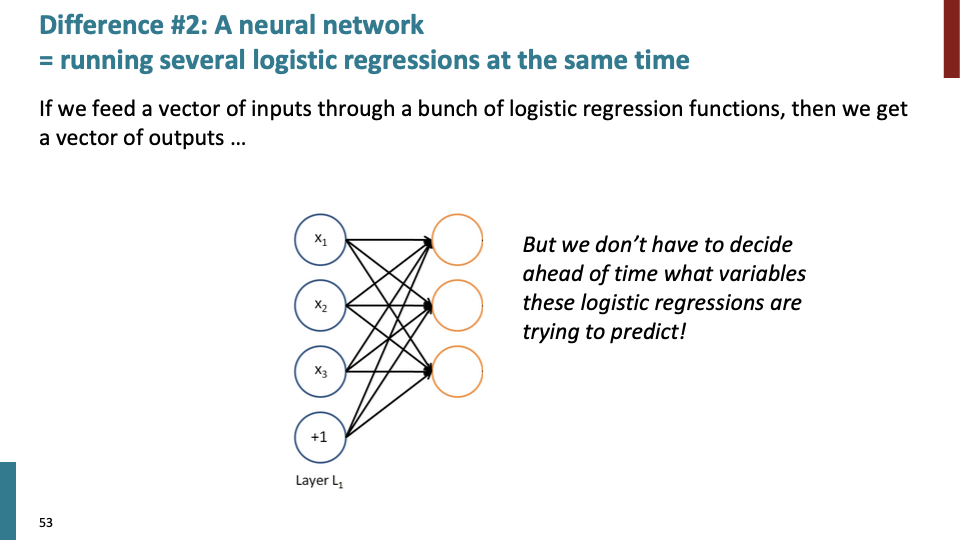
과거의 NN에서는 하나의 logistic regression에 대해서만 학습하고, a bunch of logistic regression을 동시에 하지 않았다. 사실, 우리는 logistic regression이 어떤 값을 예측하는지에 대해서 미리 결정할 필요가 없었다. 주황색 logistic regression unit layer가 useful한 어떠한 것을 학습한다.
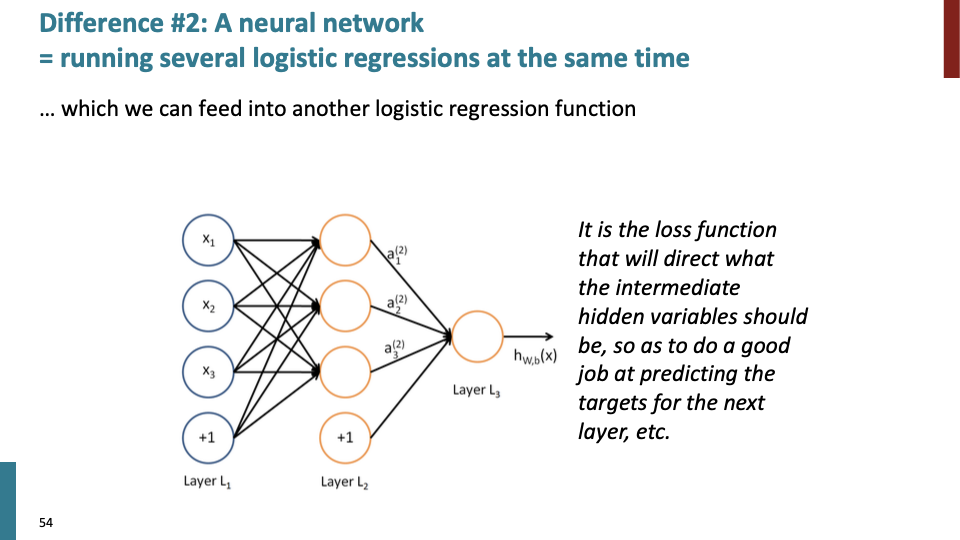
loss function이 intermediate hidden variable (주황색 unit)이 어떤것을 학습해야 하는지 direct하고, back propagation을 통해 parameter를 update하여 좋은 예측을 한다.
그리고 좀더 효율적으로 학습하기 위해 좀더 sophiscated functions of the input을 이용한다면 더 복잡한 task (ex) speech recognition) 도 할 수있다.
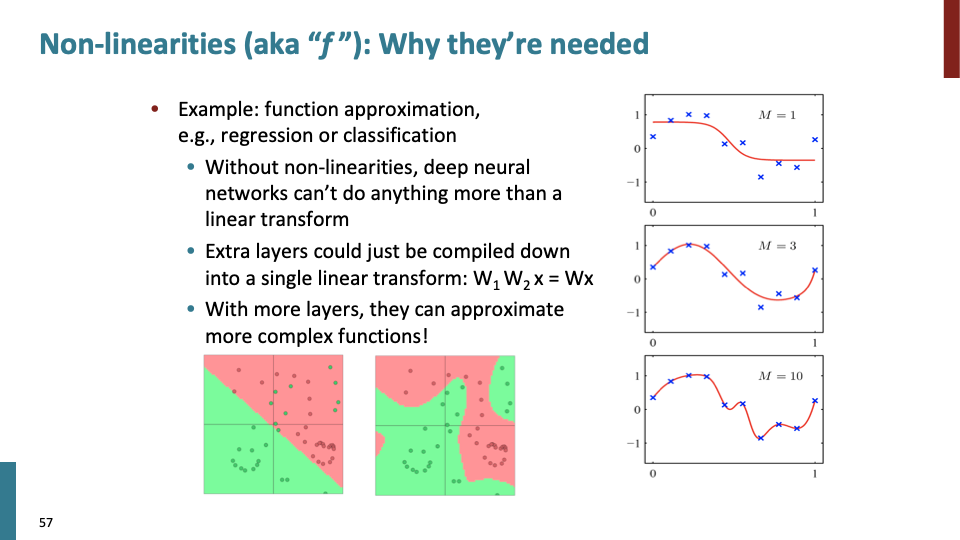
Active function으로써 non-linear function이 필요한 이유에 대한 내용이다. non-linear한 더 복잡한 boundary를 구할 수 있다.

NER(Named Entity Recognition)의 task는 text의 name을 찾아서 classify하는 일이다.

많은 entity들은 mutli-word term이고, 어떤 entity인지 말하는 가장 간단한 방법은 같은 분류인 sequence를 같은 entity로 본다. BIO encoding에 대해서는 나중에 수업한다고 하셨다. 아래는 간략한 BIO encoding의 설명이다.
개체명 인식에서 코퍼스로부터 개체명을 인식하기 위한 방법으로는 여러 방법이 있지만, 여기서는 가장 보편적인 방법 중 하나인 IOB (또는 BIO) 방법을 소개합니다. B는 Begin의 약자로 개체명이 시작되는 부분, I는 Inside의 약자로 개체명의 내부 부분을 의미하며, O는 Outside의 약자로 개체명이 아닌 부분을 의미합니다.

NER problem은 처음에 보기엔 쉬운 것처럼 보인다. 왜냐하면 google, facebook이라는 회사 이름이 있을때 그것들이 회사라고 분류하는 것이 어려울수 없기 때문이다.
하지만 NER은 위와 같은 이유로 어렵다. “First National Bank Donates 2 Vans To Future School of Fort Smith”라는 문장을 예시로 들어 설명한다. “First”가 은행 이름에 포함되는냐도 unclear하고, “Future school”이 대명사인지, 정말로 미래 학교인지도 모른다. “Zig Ziglar”라는 unknown 단어에 대해 사람인지 무엇인지 판별할 수 없다. 또, Charles Schwab”은 90%이상 ORG로 쓰이지만, 위의 문장에서는 사람으로 쓰였다.

context에 있는 단어에 대해 classifier를 만들어 보자. “To sanction”과 “To seed”와 같이 문맥에 따라 단어의 의미가 달라진다. 즉, context를 알아야 의미를 파악할 수 있다.

아이디어는 context window의 neighboring words에 대해 각 단어를 classify하는 것이다. 간단한 방법 중 하나는 window에 있는 word vector들을 average한후 average vecotor에 대해 classify하는것이고, 이 방법은 위치에 따른 정보들이 유실된다.

그래서 더 좋은 간단한 방법은 big vector of word window를 만드는 것이다. concatenation된 word vector의 center word에 대해 classify하는 것이다. window size = 5, word vector가 d- dimension이면 5d dimension vector에 대해 분류하는것이다.

위의 논문은 초기 neural NLP에서 유명한 논문 중 하나 인데, 위에서 말한 name entity에 대해 window classification하는 아이디어를 조금 다른 방식으로 사용하였다. 다음 슬라이드에서 설명하겠다.

“Not all museums in Paris are amazing”이라는 문장을 예를들어 설명하겠다. paris라는 단어의 위치가 중가에 있을때는 높은 점수를 주고, 중간에 있지 않을때는 낮은 점수를 준다. 중간에 있지 않을 경우를 “Corrupt” window라고 한다.

score를 classifier에 넣기 전의 값으로 사용한다.

multivariable에 대한 gradient를 계산할때, fully vectorized gradient를 matirx calculus 방법이 non-vectorized gradient보다 훨씬 계산이 빠르다. (첫번째 수업때 수식으로 전개했다.)

n개의 input에 대한 m개의 output이 있을때, m x n 행렬의 편미분 행렬이 자코비안 행렬이다.

one-variable function일때와 동일하게 자코비안을 곱하며 chain-rule을 적용한다.

${ \partial \over\partial z_j}f(z_i)$에서 i=j인 경우를 제외하고 모두 0이다. 위의 자코비안의 곱은 대각행렬(diagonal matrix)의 결과가 나온다.

위의 식은 bias에 대해 back propagation하는 식이다.

위의 식은 weight에 대해 back propagation하는 식이다.

분야별로 사용하는 convention이 다르지만 input과 같은 shape의 자코비안을 사용하는 shape convention을 사용한다.