CS224N|Lecture 2 Word Vectors and Word Senses
05 Aug 2021
이번 시간에는 word2vec에서의 stocastic gradient descent의 의미, negative sampling, Glove의 등장배경과 원리, intrinsic evaluation과 같은 내용을 배웠다. Suggested reading으로 수업시간에 사용된 논문이 첨부되어있다.

Lecture 2에 대한 전반적인 목차이다. 4번 목차 : count based approach to capturinng meaning and how do they work. 6번 목차 : how do we evaluate + how do we trust our evaluation? 에 대한 내용이다.
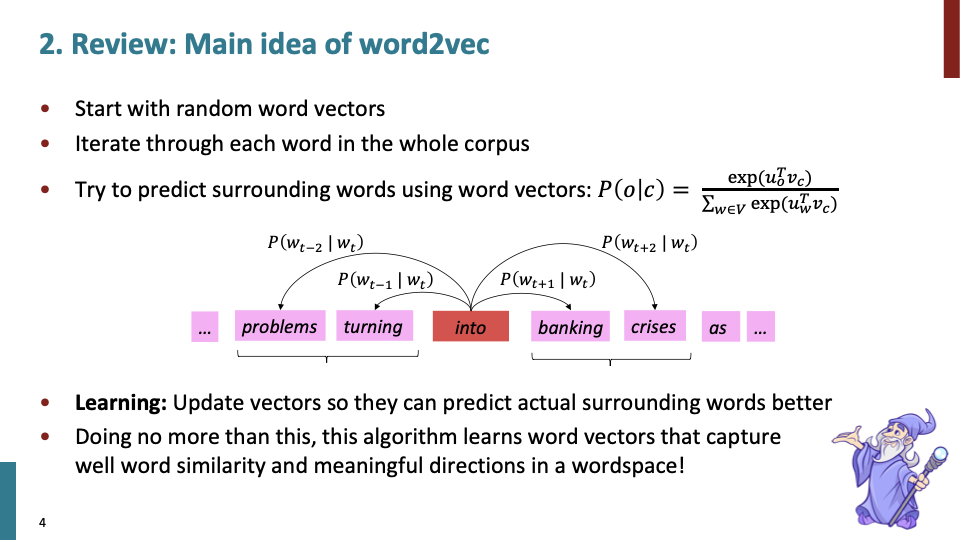
저번 수업시간에 배운 내용이다. 다음은 Word2vec의 간단한 요약이다.
iterative updating alogrithm을 통해 vector representation of word를 학습한다. move posistion by position through corpus and each point we have a center word and predict word around it to have probablity distribution. softmax의 형태의 꼴로 확률분포를 계산하고, 좋은 예측을 할 수있도록 vector를 계속 바꾼다.
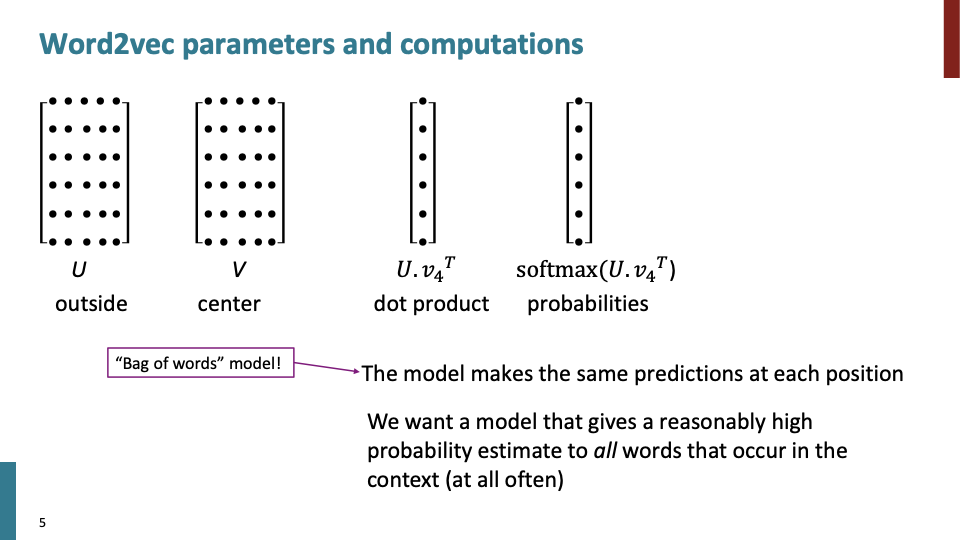
U : context word vector, V: center word vector에 대한 matrix이다. 하나의 word vector는 한개의 row로써 나타난다. 즉, U와 V는 각각 6개의 단어를 의미한다.
$v_4^T$ : particular center word를 의미한다.
$softmax(U.v_4^T)$ : probability distribution over words in the context를 의미한다.
Bag of words model : 단어들의 순서는 전혀 고려하지 않고, 단어들의 출현 빈도(frequency)에만 집중하는 텍스트 데이터의 수치화 표현 방법
Bag of words model은 사실 각 posistion당 같은 prediction을 한다. 하지만 우리는 context에 나타나는 모든 단어에 대해 합리적으로 꽤 높은 확률로 예측을 하고 싶다.
like, the, and, of 와 같은 단어들은 자주 발생한다. 즉, 모든 단어들은 like, the, and, of와 같은 단어들에 대해 high dot product값을 갖는다. 이후 슬라이드에 나오겠지만, Aora의 논문에서 high frequeny effect를 고정함으로써, semantic similarities에 대한 성능이 더 좋아지는 것을 볼 수 있다.

word2vec은 비슷한 단어를 vector space에 가깝게 둠으로써, objective function의 값을 최대화 한다. 하지만 high dimensional vector space의 대부분 특성들은 very unintuitive하다는 것이다. 즉, 단어들은 서로 다른 많은 방향에 대해 많은 단어들과 가까워 질 수 있다.
예를들어 그림에서 2D로 visualize한 결과 samsung과 nokia가 가까운것을 볼수있고, 만약 high dimension 이었다면 nokia는 finland와 같은 단어와도 가까울 것이다.
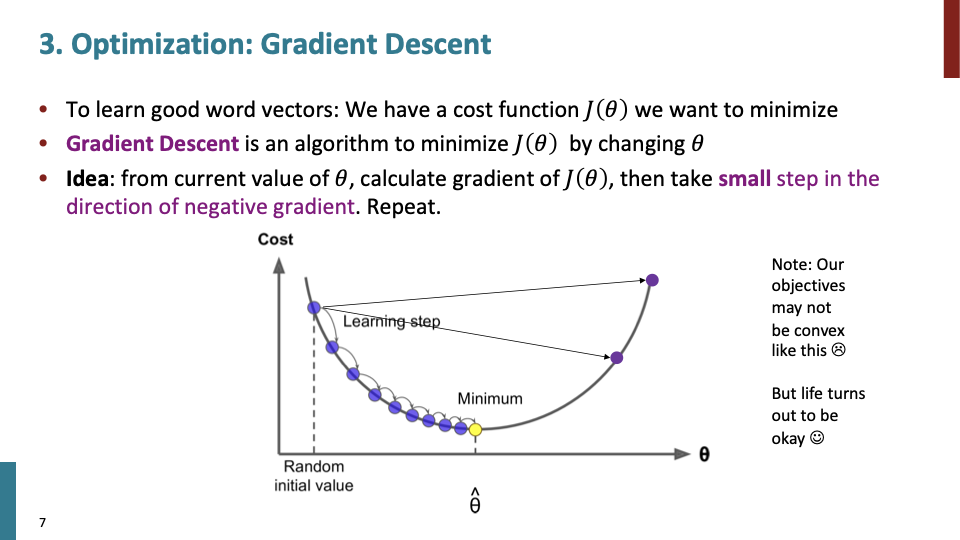
optimazation에 대한 간략한 내용이다. 관심있으면 stephen boyd 수업들으라고 하셨다. (찾아보니 convex optimazation에 대한 OCW가 있었다.)
low dimension convex function에 대한 gradient descent이므로 위와 같이 smooth한 그림이 나왔지만, high dimensional space의 non-convex curve에서는 smooth curve가 아닐 것이다.

alpha = learning rate or step size이다.

object function $J(\theta)$는 function of entire corpus이다. 만약 billion word를 모아서 word vector를 만들때, billion center word와 그에 따른 10 billion context word (fixed window size =5)에 대해 softmax 계산을 한 후에 gradient 계산을 해야한다. 즉 너무 느리다.
SGD(Storchastic gradient descent)가 그에 대한 해결책이다. simplest한 case로 sample window를 정하여 gradeint descent를 계산한다. 하지만 예를들어 한개의 window를 사용한다면, 굉장히 noisy estimate of gradient가 될 것이다. 그래서 sample size as small batch (32 or 64)로 정한다. → mini-batch라 부름.
2가지 이점이 있다.
- less noisy estimate of gradient : 각 batch에 대해 average하기 때문이다.
- 더 중요한 것으로, GPU를 사용하고, 게산을 좀더 빠르게 하길 원할때, 같은 연산에 대해 parallelization of doing same operation in a whole bunch와 같은 이점을 mini-batch를 사용함으로써 얻을 수있다.
32,64와 같은 batch size를 사용하면 42와 같은 아무 숫자보다 좀더 speed up된다. (이유는 찾아봐야할 듯, 나도 그냥 쓰고 있었다.)

stochastic gradient을 computer vision에서 사용하는 것과 word vector에 사용하는 것은 다른점이 있다. mini-batch only has only relatively a handfual of words. 예를들어 window size=10 이고, mini-batch=32 라면, 대략 100~150의 different words만 고려하여 학습된다. 하지만 million 개 이상의 모델을 만들고 싶을 것이다.
그리고, 이렇게 만들면 object function의 gradient의 matrix값들이 대부분 0이고, 매우 sparse할 것이다.

위에서 말했다 시피, 실제 나타나는 word에 대한 값만 update하게 될것이다. 좀더 똑똑한 방법으로는 multiple computer로 distributed computation을 사용해서 parameter들을 share할 수도 있을 것이다.

Q. 왜 center, context vector 인 2개 vector를 사용할까? A. 수학(계산)을 쉽게 하기 때문이다. 한개의 vector로 구현이 가능하다. 하지만 같은 방식이지만 훨씬 복잡해진다.
Word2vec에는 2가지 모델이 있다.
- Skip-grams(SG) : one center word, predict all words in a context. → 지금까지 배운 방법.
- Continuous Bag of Words (CBOW) : got all of outside word, predict center word. → 이것을 사용한다면 naive bayes modeling처럼 각 pair에 대해 독립적으로 예측한다.
추가적으로, context word에 대해 확률을 예측 할때, 모든 단어를 합쳐서 그들의 확률 에측에 사용한다. → 느리기때문, practice에서는 나쁘다.

negative sampling 또한 Tomas Mikolov가 만들었는데, 핵심 아이디어는 다음과 같다. actual observed word(분자에 있는 단어)에 대해 최대한 높은 probability를 주고, 그 다음 randomly sample a bunch of words(not actually seen words = negative sample)를 한후, 가능한 low probability를 준다.

여기선 minimazation이 아닌 maximazation이다. object function에서 첫번째 항은 observed word에 대한 것으로, sigmoid에 대입한후 log를 취한다. 두번째 항은 negative sample에 대한 항이다.

$u^T_ov_c$ (=observed context word)에 대해서 big as possible, $u_k^Tv_c$(=Randomly chosen k words)에 대해서는 small as possible. k=10 or 15의 값이 꽤 잘 작동한다.
또한 매우 frequent words ((ex) the, like, a, etc)에 대해 sampling distribution을 제안한다. 이것들에 대해 sample하는 첫번째 단계는 unigram distribution을 사용하는 것이다.
unigram : large corpus에서 단어를 가져오고, 각 단어가 얼마나 자주 발생했는지 count up한다. 그 값이 unigram count이고, 이 값에 대해 3/4승을 취해준다. $U(w)^{3/4}$ 는 very common words들이 얼마나 자주 sample되었는지에 대해 감소시켜주고, 거의 발생하지 않는 단어의 count에 대해 increase해준다. Z는 normalization term으로, 합이 1이되어야 probability distribution이 되기때문에, Z로 나눠준다. 추가적인 질문으로써, 3/4, window size와 같은 값들은 hyper parameter로써 휴리스틱하게 정해진것이다.
(학생 질문) mini-batch하는것이 left to right하는것보다 좋은이유는 하나 더있다. 최신 pakage인 tensorflow, pytorch에서는 처음에 학습하기전에 shuffle operation을 사용하여, 각 epoch당 data를 shuffle 한후 word2vec을 만든다. locality와 같은 이점이 있어 더 빠른 faster computation이 가능하다.

왜 co-occurence count를 바로 계산하지 않고 word2vec처럼 계산을 할까? big pile of text가 있고, 모두 누적하여 특정 단어의 개수를 다 세고, prediction에 바로 사용하는게 합리적인 것처럼 보인다. 이러한 방법은 distributed representation technique까지 포함해서 모두 옛날 연구의 내용이다.
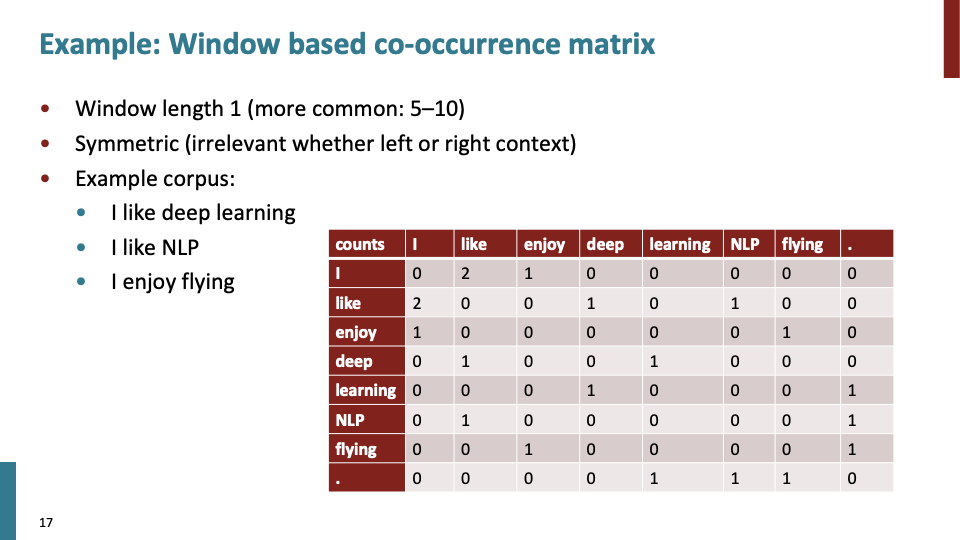
window length로써 간단하게 예시를 들기위해 1로 잡았다. word2vec에서 그랬듯이 symmetric 하므로, left,right는 무시한다. 위의 table은 big huge sparse matri로써 word occurence count에 대한 내용이다.
이 값들로 similarity of the vector directly in terms of co-occurence count를 계산할 수 있다. 만약 단어가 million개 이상이라면 cell이 trillion 이상일 것이고, 많은 storage를 요구한다. 만약 대부분 cell이 0인 것을 알고 있다면, sparse matrix(희소 행렬) representation을 사용하여 용량을 덜 사용할 수 있을 것이다.

problem은 simple count co-occurence vector에 있는 3가지이고, 그에 대해 traditional answer이 low-dimensional vector의 내용이다.
그렇다면 나오는 질문이 어떻게 dimensionality를 줄일 것인가이다. 간단하게 말하면 대부분의 정보를 preserve하는 correspoding low dimensional matrix를 찾는 것이다.
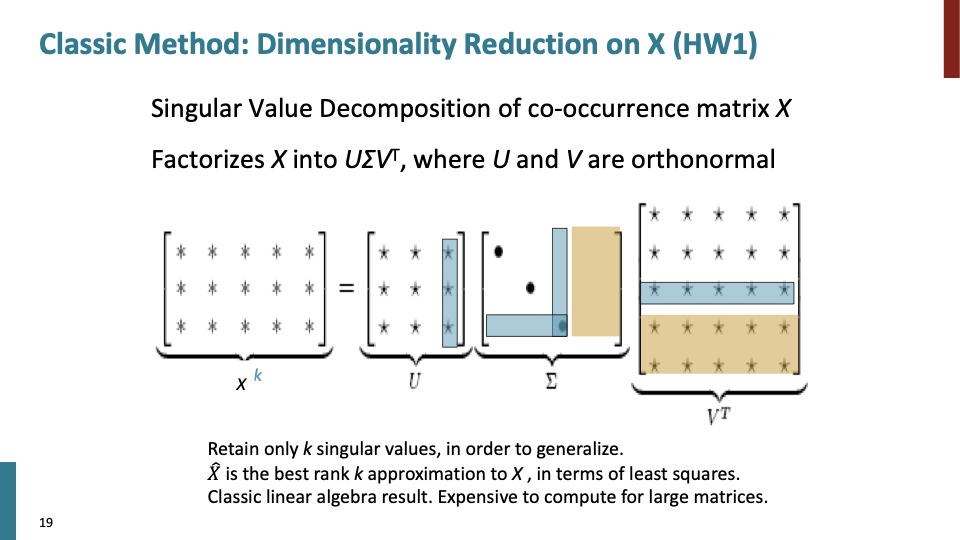
SVD는 직교하는 벡터 집합에 대하여, 선형 변환 후에 그 크기는 변하지만 여전히 직교할 수 있게 되는 그 직교 집합은 무엇이고, 그리고 선형 변환 후의 결과는 무엇인가 에 대해 찾는 방법이다. 분해되는 과정보다는 분해된 행렬을 다시 조합하는 과정이 위에서 차원을 축소할때 사용된것이다. 기존의 $U,\sum,V^T$로 분해되어 있던 A행렬을 특이값 p개만을 이용해 A’라는 행렬로 ‘부분 복원’ 시킨 할 수 있다. 위에서 말했던 것 특이값의 크기에 따라 A의 정보량이 결정되기 때문에 값이 큰 몇 개의 특이값들을 가지고도 충분히 유용한 정보를 유지할 수 있다. reference : SVD
Standard most common way of doing dimensionality reduction으로써, Singular Value Decomposistion(SVD)를 사용하여 차원을 축소한다. 어떠한 matrix라도 가능하고, 3개의 matrix로 decompose한다. 가운데 있는 $\sum$ 은 diagonal matrix로써, singular vecotr를 갖는다. 대각 행렬의 값은 weighting of different dimension으로, 점점 아래 행으로 갈수록 size가 작아진다. 양쪽 두개의 matrix는 가운데 matrix에 대해 각각 row와 column에 대해 orthogonal한 base를 갖는다.
특정한 경우, square matrix라면 word2vec보다 더 간단하기 한다. 보통의 경우 full orthogonal base(노란색, 파란색 부분)는 곱셈할 때 사용하지 않는다.
reduced SVD result는 least squres errors in estimation을 의미하고, 3개의 matrix 곱은 will give $X^k$: best k-rank matrix이다.
SVD로 차원을 축소시켜 분석하는 방법을 Latent Semantic Analysis(LSA)라하고, 20세기-21세기 넘어갈때,가장 popularized한 방법이다. word application에 사용되었다.
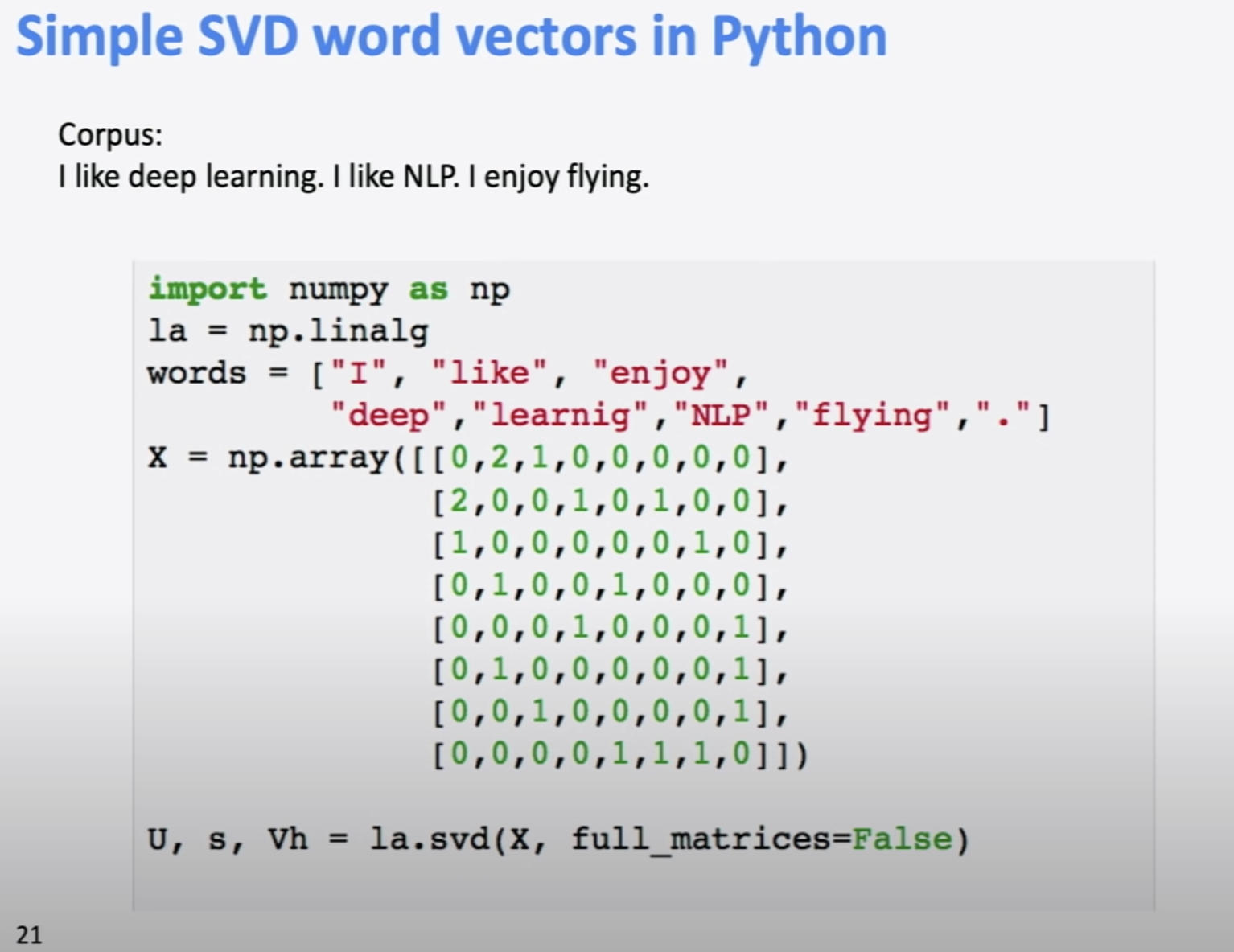
python으로 SVD를 하는 code이다.
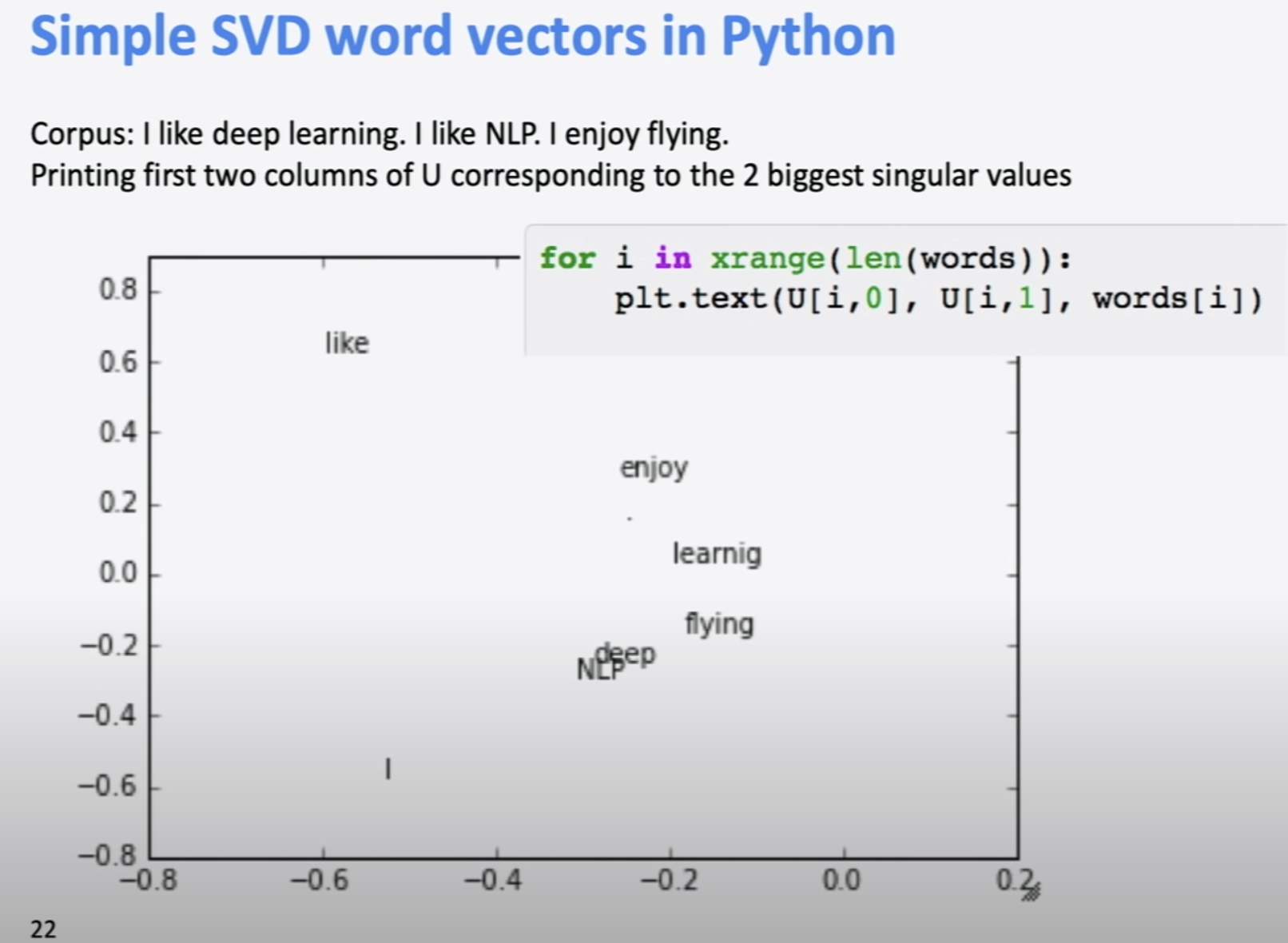
위에서 SVD word vector를 plot한 사진이다.
LSA의 idea는 low dimensional space에서 semantic direction을 찾고, 그것을 information retrieval에 사용하는 것이다. 하지만 이것 만으로는 잘 작동한 적은 없었다.

Rohde의 Hacks to X라는 논문의 내용이다. 단순히 raw count를 사용하기 보다는 count값에 대해 여러가지 값을 fiddling하자는 아이디어이다. (1) log scale (commonly used in information retrieval) (2) use ceiling function : 최소값을 예를들어 100으로 정해서 올림한다.
그리고 word2vec에서 whole window가 아니라 center word에 가까운 단어에 대해 고려했던 것처럼, 더 가까운 단어들에 대해 count한다. 그리고 count값이 아닌 pearson correlation을 사용했고, 음수는 0으로 만들었다.
위의 내용이 어떤 관점에서는 bags of hack으로 볼수도 있지만, 이러한 transformed count가 실제로 useful word vecotor를 만들었다는 것이다. 사실 이러한 transformed count가 다른 형태로 word2vec에 사용되고있다.
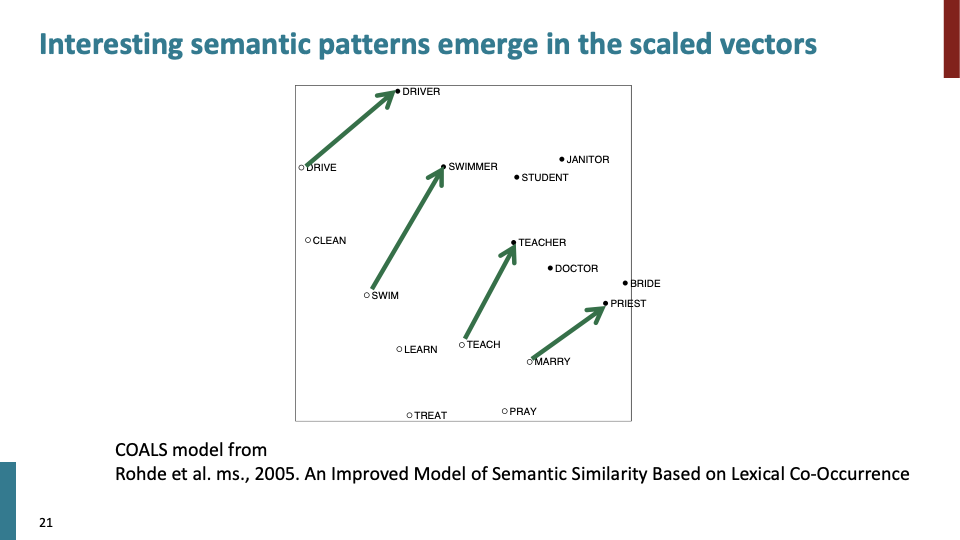
evaluating with analogy 방법은 사실 developed 된것이 아니다. mikolov가 제안했지만, 사실 Doug Rohde가 이것을 만들었다. 그는 word vector의 semantic representation을 향상시키기 위해 이런 종류의 transformation을 하였더니, 이러한 interesting property가 나타났다고 했다.
위의 그림에서 Drive → Driversemantic의 화살표를 보면 semantic vectors which are basically linear components 을 관찰 할 수 있고, 다음과 같이 말할수 있다. Roughly there’s sort of direction in the space that corresponds to verb to doer of verb. 만약 너가 linearity property를 갖고있는 vector space를 construct 할 수 있다면, analogy에 관해 잘하고 있는 것이다.
만약 너가 count에 대해 carefully control을 할수 있다면, conventional method 또한 조흔 word vector space를 제공할 수 있다. 이것이 Glove의 starting off point 였다.

GloVe는 크게 Count based와 direct prediction 관점에서 생각할 수 있다. 검은색은 advantage이고, 빨간색은 disadavantage이다.
Count based에 대한 연구는 COG pysch((Cognitive psychology : 인지 심리학)분야에서 많이 연구되었다. count based에서는 빠르게 학습되고, global statistics of whole matrix를 estimate하는데 사용하므로 효율적으로 통계를 사용한다. 하지만 word similarity를 capture하는데 만 사용되고, large count에 대해 disproportionate importance가 있었다. (Doug Rohde가 이 문제를 어떻게 풀어야하는지 보여주었긴 하다.)
direct prediction은 neural network method로써, probability distribution을 define하고 나타나는 word에 대해 predict 했다. 그리고 count based는 huge matrix를 만들어서 메모리를 많이 잡아 먹는 반면, sampling을 사용하므로 메모리 걱정이 없었다. 그리고 word similarity를 넘어서 더 복잡합 패턴 또한 capture할 수 있었다.
jeffrey pennington의 논문으로, count based와 direct predict 방법을 합쳤다. count matrix를 사용하는 반면 Neural network의 이점을 가져왔다. 그리고 효율적으로사 사용하기 위해 components of meaning이 vector space에서 linear operation에 가깝길 원한다.
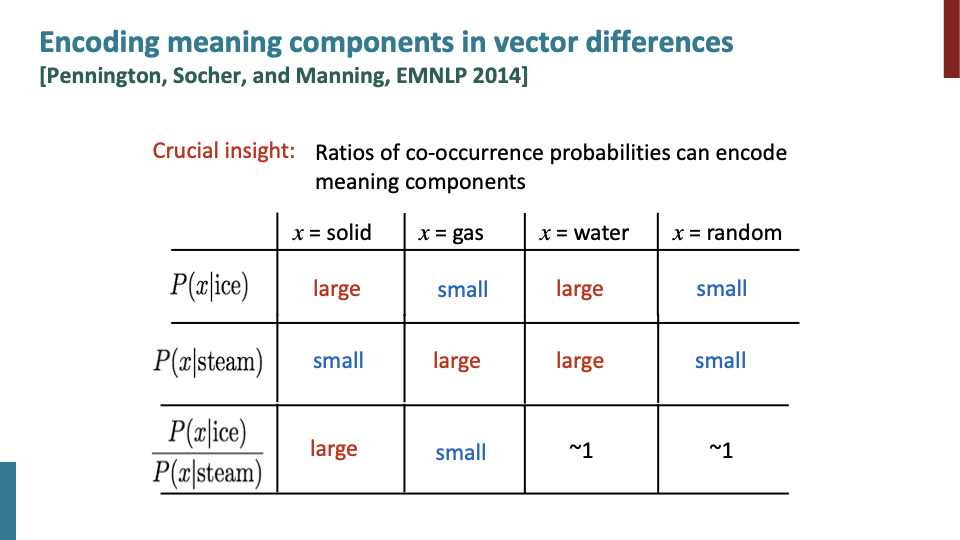
| Crucial insight는 ratio of co-occurence probablities가 meaning component를 encode할 수 있다는 것이다. $P(x | ice)$는 ice와 함께 x가 얼마나 자주 발생하는지에 대한 값이다. 단순히 large,small 값 자체만으로는 의미가 없다. 중요하게 봐야할 것은 difference of these component in a meaning. |
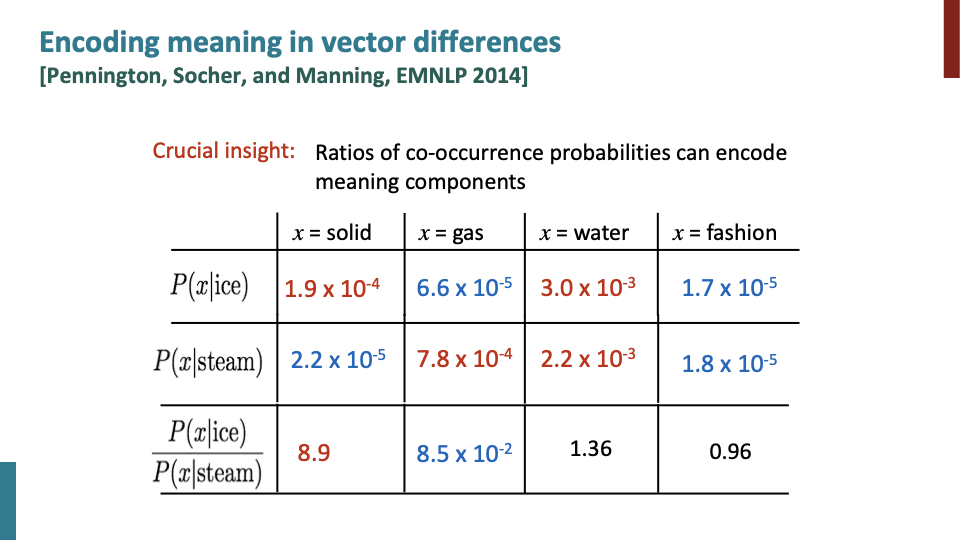
ratio of co-occurence probablity가 뜻하는 것이 dimension of the meaning이다. 1.36,0.96→ they are not the dimension of meaning. ratio of co-occurence probablity가 linear하다면 잘되고 있는것이다.

word vector space에서 linar mearning component로써 ratio of co-occurence probablity를 어떻게 capture할까에 대한 내용이다.
$w_a-w_b$ : vector difference가 ratio of co-occurence probability가 된다.

object function에서 두번째 항부터 보자. dot product과 log of co-occurence probability가 최대한 similiar해야 한다. 실제로는 같지않아 어느정도 loss가 있고, bias term을 두개의 단어에 대해 넣는다. 그 다음 성능을 좋게 하기위해 첫번째 항이 $f(X_{ij})$를 추가 했다. capping effect로써 very common word pair에 대한 항이다.
이것이 Glove model of word vector이다. preceding literature들은 count base or prediction method 둘 중 하나였는데, GloVe가 이 2가지를 합쳤다. good word vector얻기 위하여 count matrix로 예측하고 비슷한것에 대해 iterative loss based estimation method used for the NN method을 사용했다.

다른 단어이지만 frog와 비슷한것을 찾을 수 있었다.

이제 evaluation에 대해 얘기할 차례이다. 보통 NLP에서 evalutation에 대해 얘기할때, 처음 나오는 것은 intrinsicc versus extrinsic evaluation이다.
intrinsic evaluation은 간단하게 말하면 how good a job did you get에 관한 것이다. 예를들어 동의어들을 가깝게 배치했는지, 잘 예측하는지 보는 것이다. 매우 쉽고, 빠르게 계산할 수 있으며, system을 이해하게 도와주기 때문에 useful한 tool이다.
extrinsic은 not clear하다. 이러한 new stuff를 real system에 사용할때 이 방법을 사용한다.
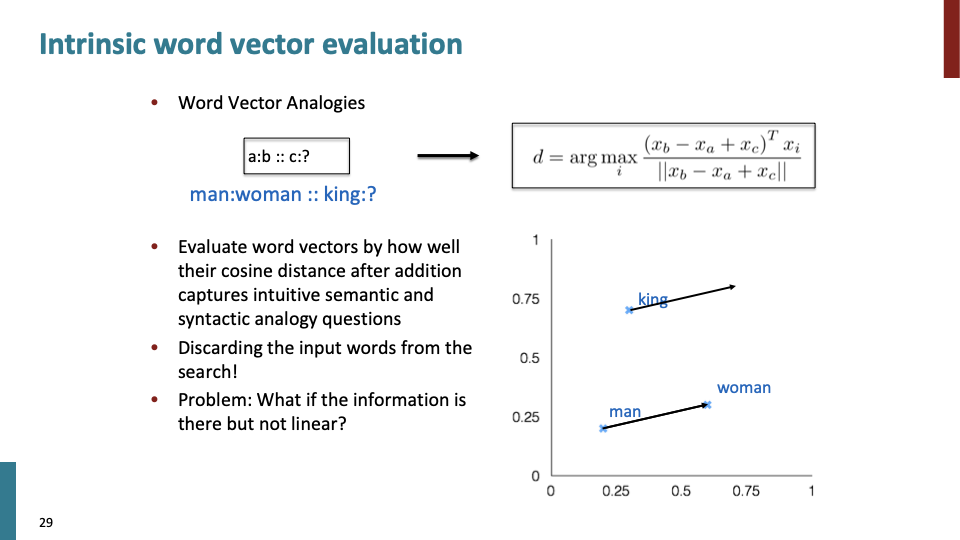
Different word candiate에 대해 cosine distance and angle을 측정하여 analogy를 capture하기도 한다. 또는 system을 forbid하여 input word를 버리기도 한다.
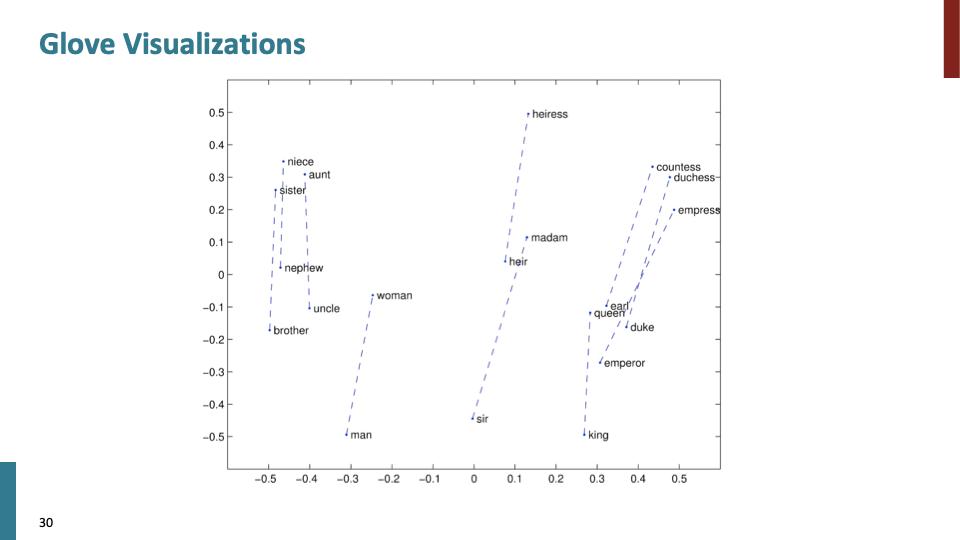
GloVe visualization은 Doug Rohde가 발견한 analogy work과 완전히 동일한 linear property를 보여준다. 위의 그림은 gender display에 관한것이다.
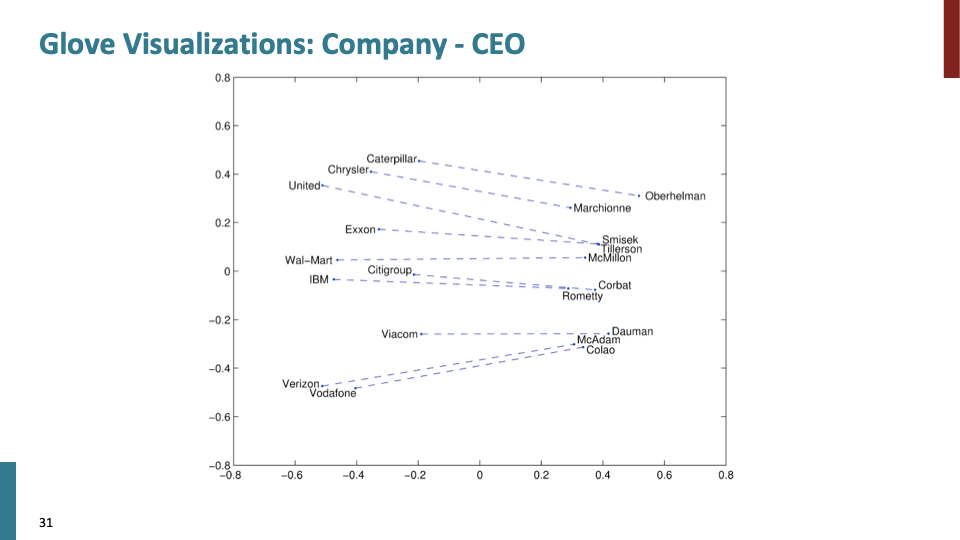
company-CEO에 관한 것이다.
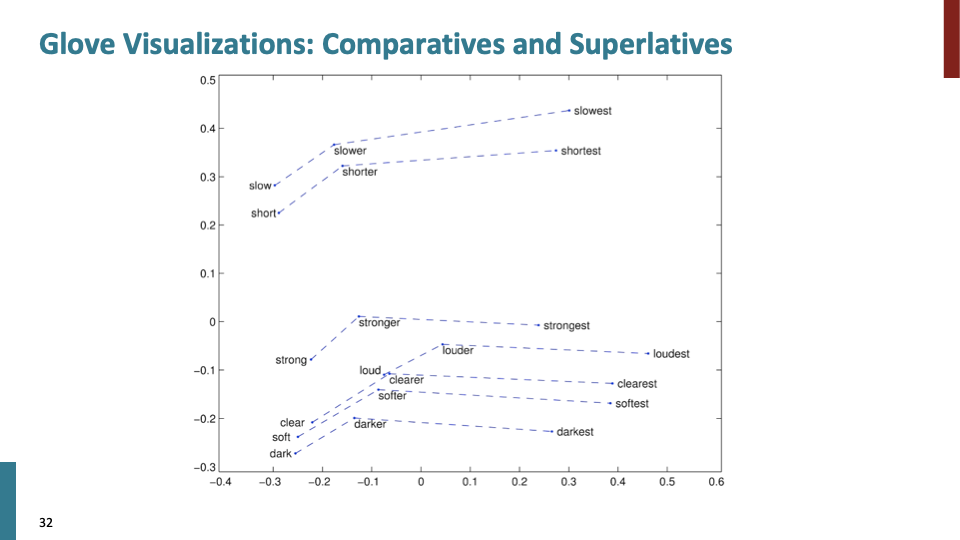
more syntactic fact에 관한 것이다.

Mikolov가 dataset을 이용해 많은 analogy task를 한 내용이다.
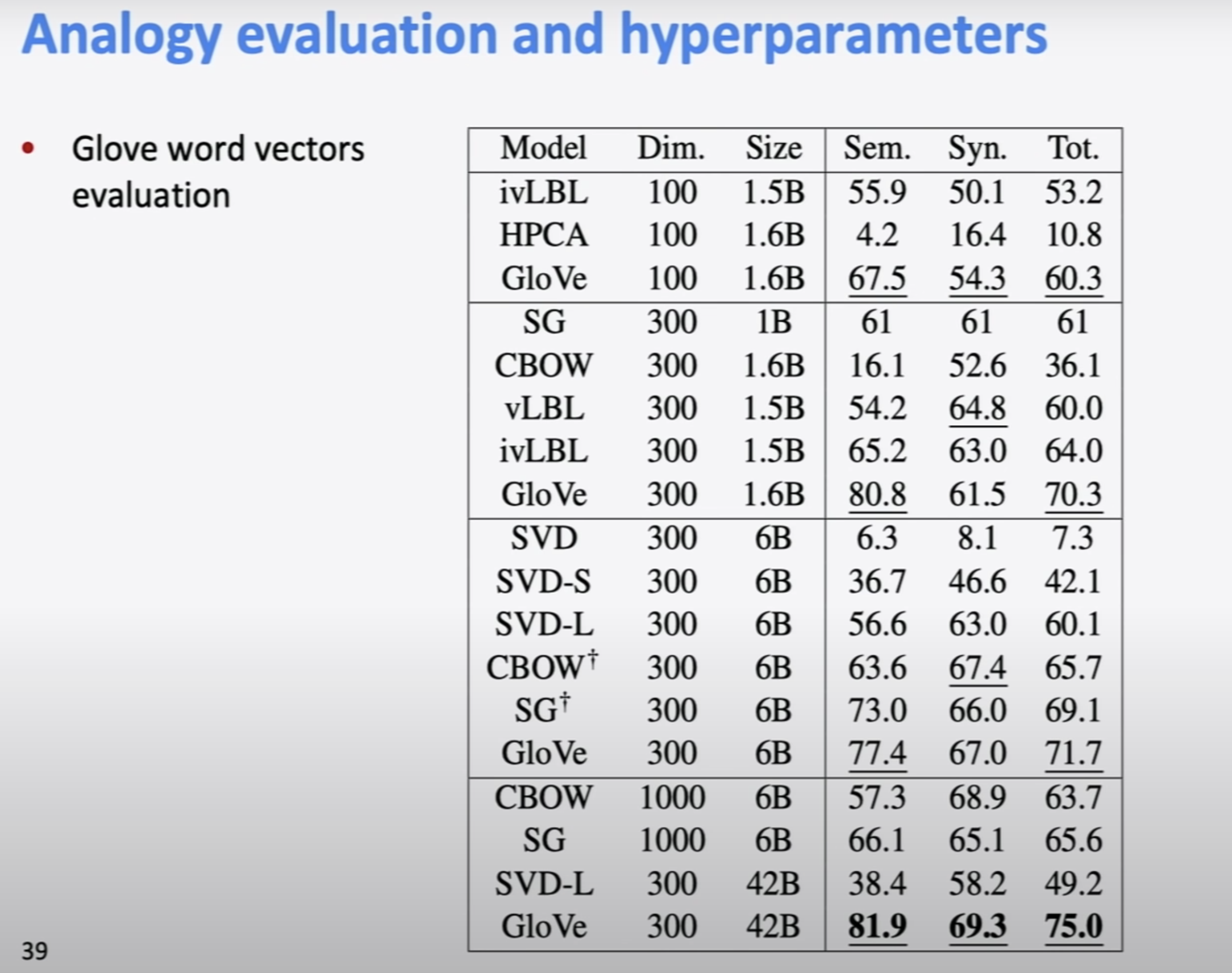
GloVe paper에 나온 table이고, 놀랍지 않게 GloVe가 가장 잘 작동한다. (그들의 논문이니 ㅋ) 중요하게 봐야할 것은 plain SVD on count는 매우 안좋다.(6.3/8.1/7.3) Doug Rohde가 보여줬듯이 before SVD manipulation of count matrix하는 것은 꽤 잘 작동 한다.
amount of text 또한 성능에 영향을 주고, big amount of text에서는 당연히 big dimensionality가 더 잘 작동한다.
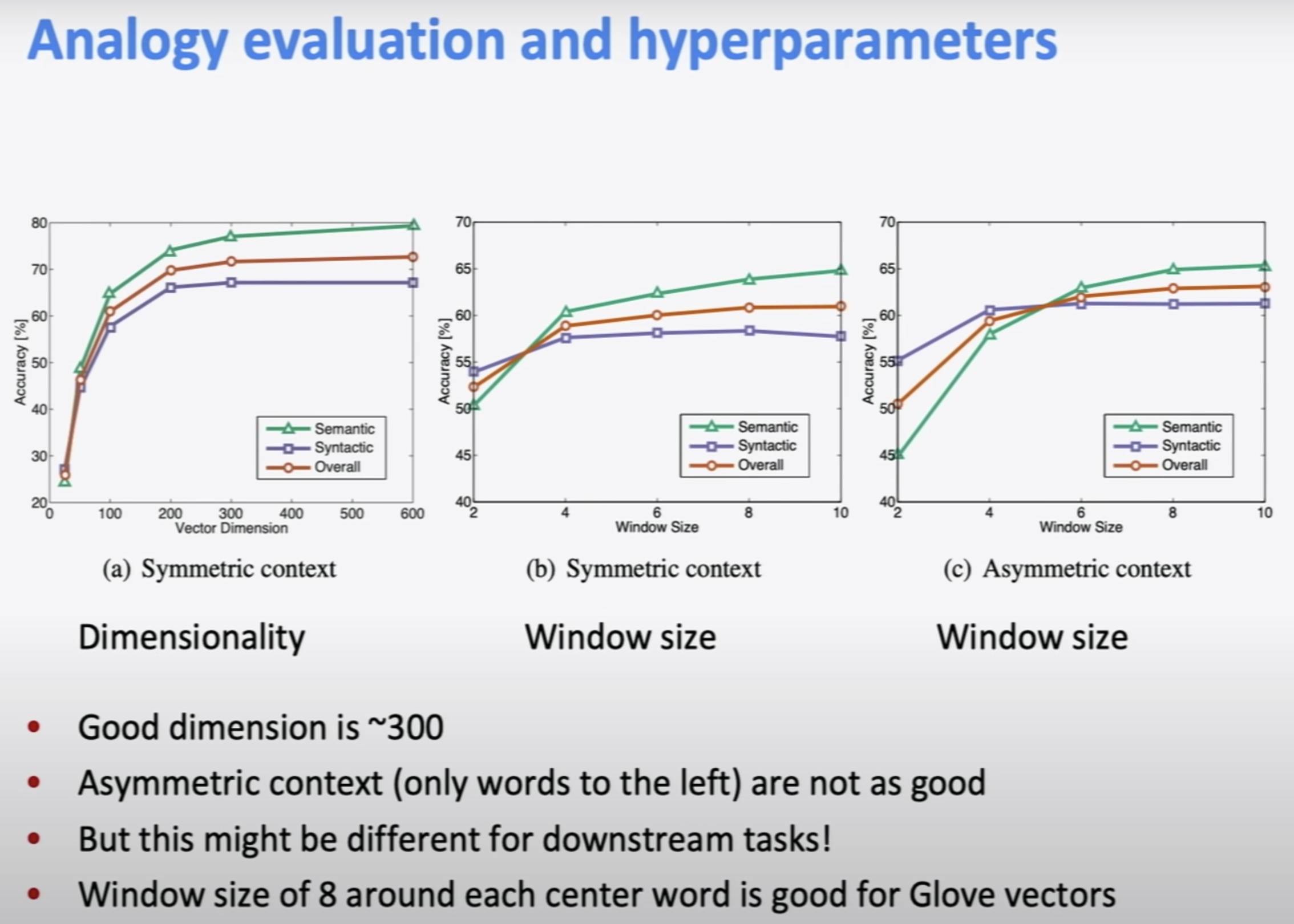
(a) : graph of dimensionality and what the performance is. dimension = 300까지는 꽤 증가하고, 그 이후로는 거의 flat하다. 그래서 많은 word vector가 300 dimension을 사용한다.
(b) : window size = 2일 경우에는 syntactic effect가 very local한 효과이므로 더 높다. 증가할수록 semantic effect가 더 좋아진다.
(c) : Asymmetric으로, 한쪽 side에서만 context를 사용하면 성능이 좋지 않음.
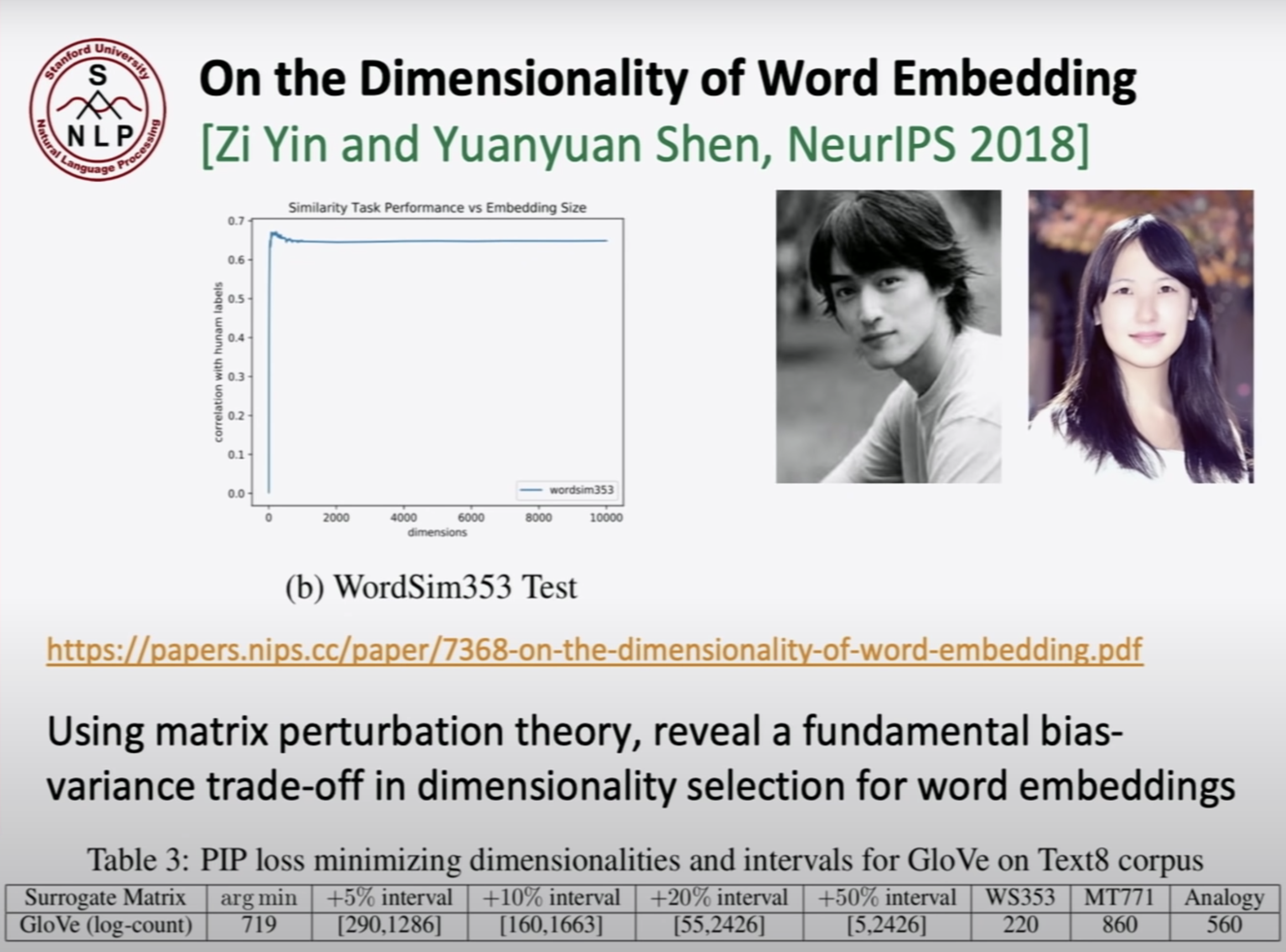
matrix pertubation theory를 사용하여 bais와 variance trade-off하여 word vector의 dimensionality selection을 한 연구이다. 이 paper에서는 0 부터 10,000까지 word dimension을 사용했다. 200~300에서 performance가 최적인것을 발견했다. 만약 10,000 차원을 사용한다면 dataset의 개수에 비해 parameter수가 너무 많아 성능이 fall apart할 것이다.
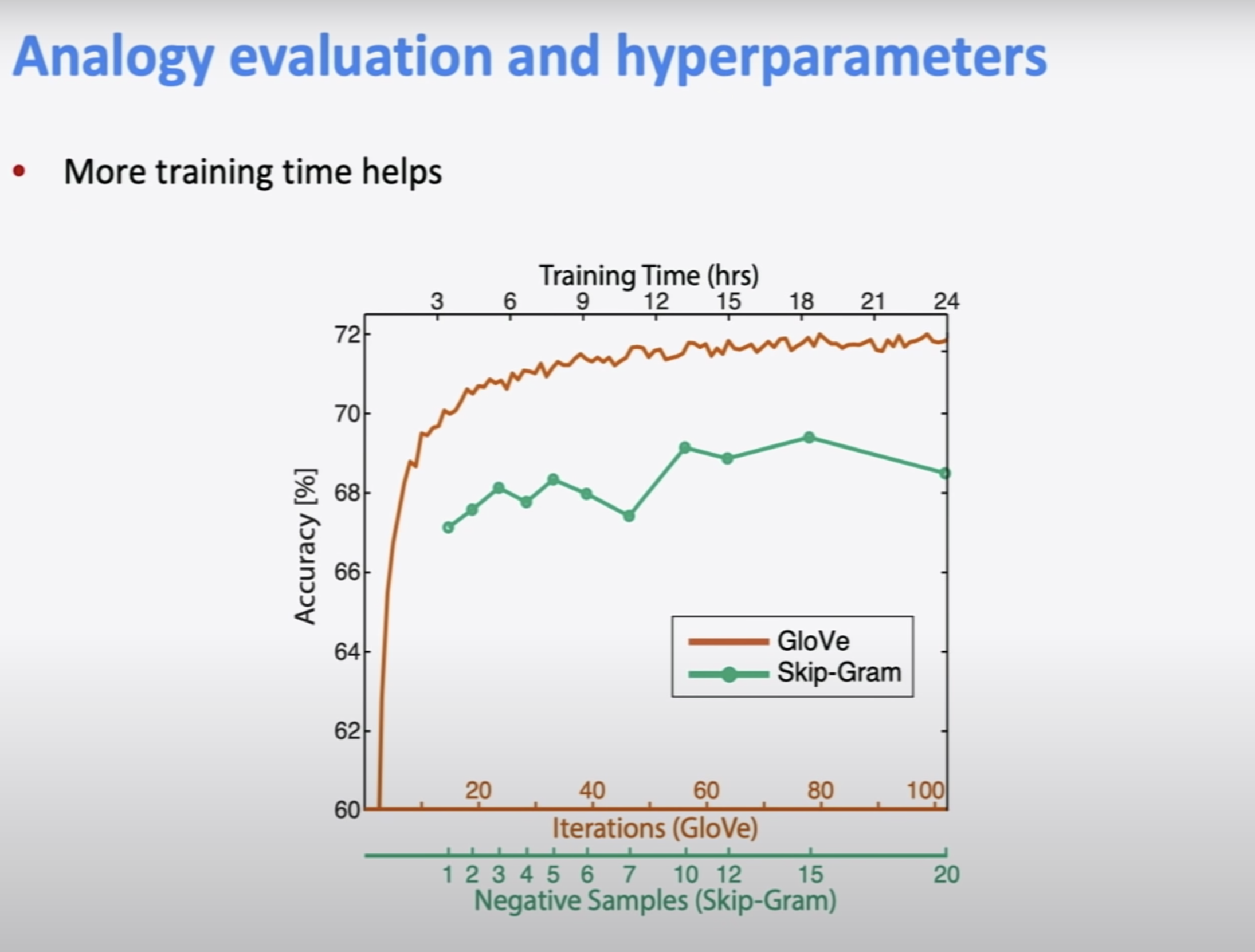
당연히 학습할수록 성능이 좋아진다. 그리고 학습하는데 시간이 많이 걸리니깐 숙제를 미리 하라고 하셨다.
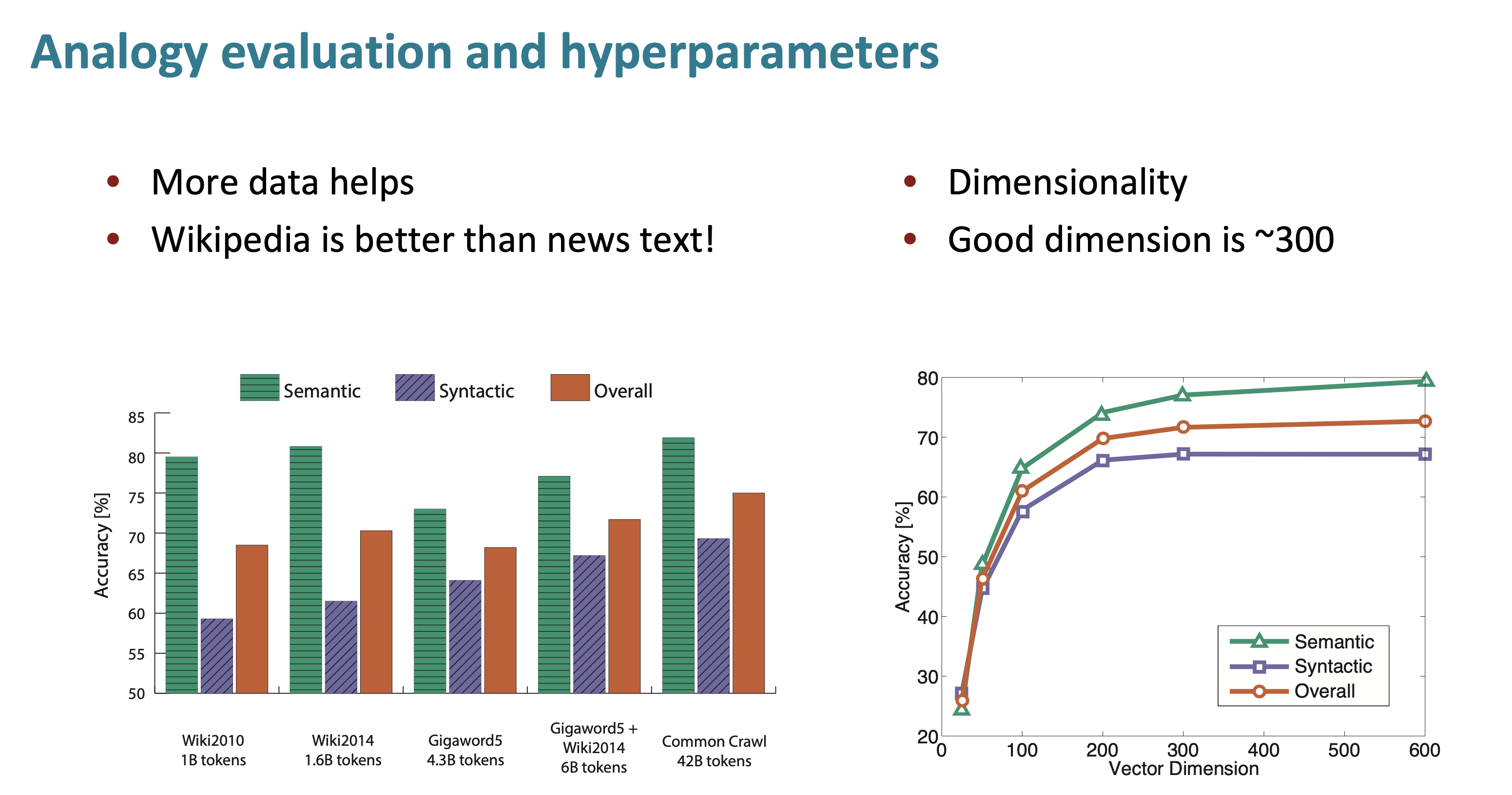
wiki2014의 성능이 gigaword5(news)보다 좋다. wiki가 encyclopedia(백과사전)에 더 가까우니깐 이러한 성능 차이를 본것같다. (옆의 그림은 앞서 나온 슬라이드와 겹친다.)
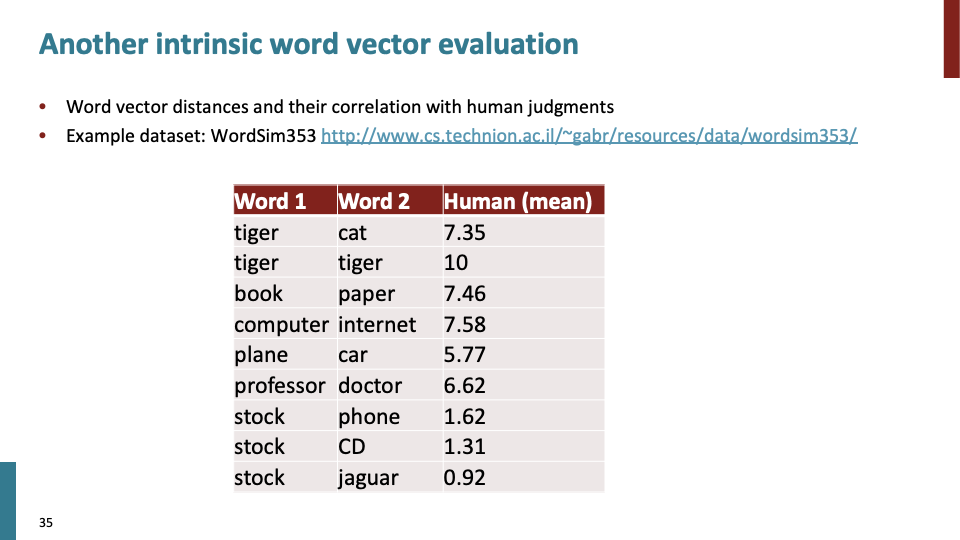
다른 basic evaluation이다. caputring similarity judgements로써 심리학에서 작은 literature 중 하나로, 사람들이 similarity에 대해 1~10사이의 점수를 human judgement로서 매긴다. 그리고 이 값을 vector space에 mapping하여 evalutation한다.
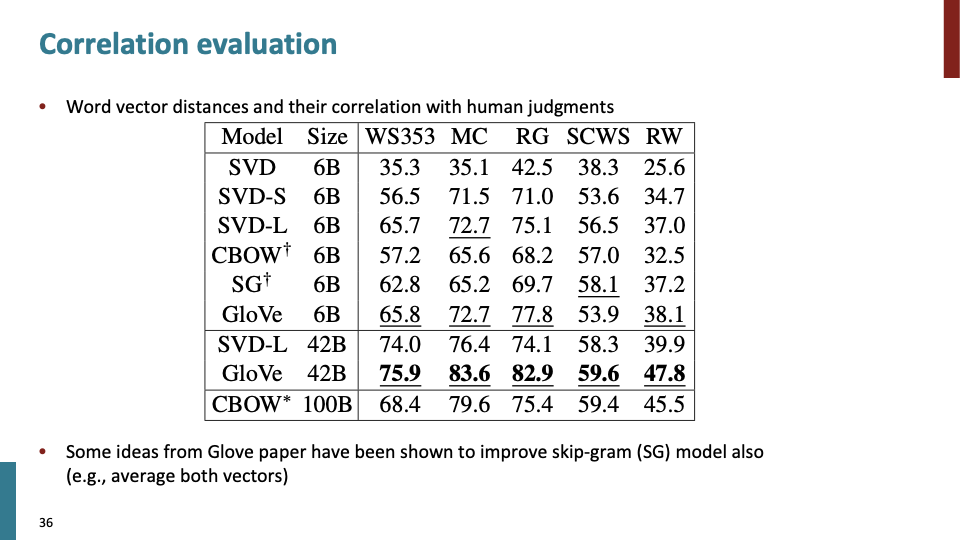
correlation evaluation에 관한 table이다.

by and large(대부분), human language의 word는 ambiguous하고 많은 의미를 담고 있다. common words에서는 더욱이 진실이다. (하지만 technical word에서는 not true)
예를들어, pike는 fish, large spear, road, gymnetic move 등 과 같은 의미를 갖고 있다.

위와 같은 lots of meaning을 담고있고, pike 뿐만 아니라 많은 common word들은 많은 의미를 갖는다.
Q. 그렇다면 how can do this work if we just have one meaningful word?

word2vec이 나오기전에 back in 2012에 사람들이 관심이 이것에 대해 관심이 있었다. 한가지 단어에 대해 여러 sense(의미)를 갖는 모델에 대한 아이디어를 떠올렸고, crude way로 그것을 구현했다. 각 common word에 대해 발생하는 context에 대해 cluster한다. 그 단어에 대해 여러개의 multiple cluster가 있다면 psedudo word로 split하는 아이디어이다.
예를들어 jaguar에 대해 5개의 cluster가 있다고 하자. jaguar1, jaguar2, jaguar3, jaguar4, jaguar5가 있다 라고 하고 어떠한 vector alogrithm을 돌려 split 한것이다. 동작은 했지만, crude하고 문제가 많았다. sense(의미) 사이의 division이 not clear했다. 많은 sense들이 서로 relate되고 overlap 되었다. 이러하 이유는 사실 단어의 sense들은 radom하게 정한것이 아니라 어떤 또 다른 sense를 stretch하여 생긴것이기 때문이다.

한개의 단어가 여러 word sense있을때 해결법인 Sanjeev Arora의 논문이다.
word vector는 superposistion of vector of different sense으로 표현된다. superposistion은 단순히 weighted average를 의미한다. 만약 단순히 이 word vector에 대해 average를 한다면, average말고 얻을 수 있는게 없다고 생각할 수 있다. 가령 두개의 합이 54인 숫자 두개를 맞춰보라고 하면 맞출 수 없다.
하지만 word vector에 관해 얘기하면, high dimensional vector space는 매우 vast하여, space에서 actual word or sense들은 매우 sparse하다. sparse coding에 의거하여 sense들을 separate out할 수 있다. 즉, components of superposistion을 reconstruct할 수 있다.
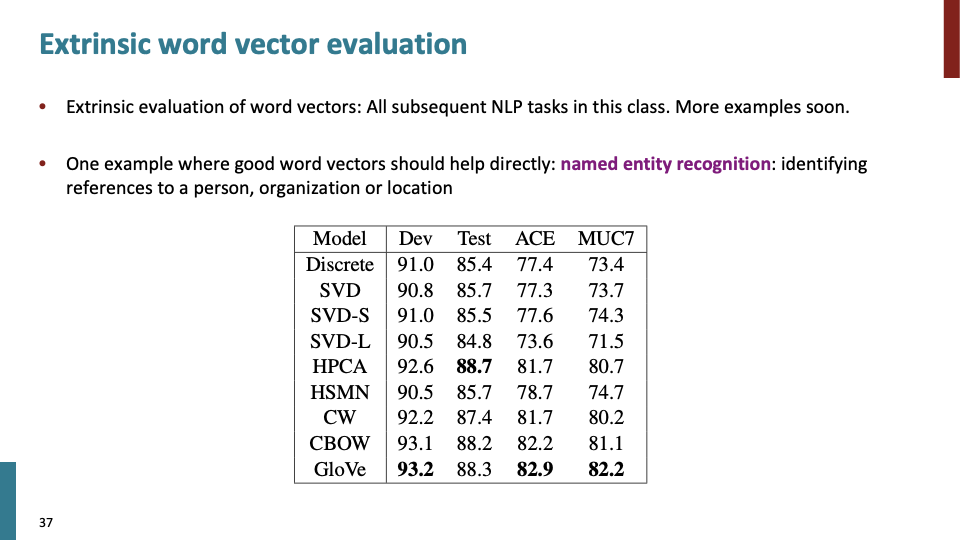
지금까지는 intrinsic evaluation이다. 이제 extrinsic word vector evaluation에 대해 설명한다.
근데 사람들이 NLP분야에서 word vector에 excited할까? 그 이유는 그들의 task를 매우 향상시키기 때문이다. 한가지 예시로 Named Entity Recognition(NER) task로 good word vector가 직접적으로 성능을 향상 시킨다.