트리(Tree)

29 Jul 2021

CTP 알고리즘 동아리에서 여름방학 코딩테스트반에 참여하여 공부한 내용입니다.
아래 자료는 수업에서 사용한 내용입니다.

트리는 자료구조 그래프의 부분집합으로써, 특이한 성질이 있어 일반적인 그래프와 달리 할 수 있는 일이 많다.

트리의 조건

연결 그래프이다 임의의 서로 다른 두 정점을 잇는 경로가 존재한다.
사이클이 존재하지 않는다. ( 간선의 방향 무시) 앞서 언급한 경로는 어떤 두 정점에 대해 하나만 존재한다.

용어

깊이 : root에서 출발했을때 지나야하는 간선수
높이 : 최대 깊이 또는 1을 더하기도 함
부모-자식 : 인접한 두 노드에 대해 루트에 가까운 쪽이 부모
리프노드 : 자식이 없는 노드
서브트리 : 트리에 포함된 트리

트리의 성질

간선 개수는 반드시 노드 개수보다 1 적다
루트 노드를 제외한 모든 노드는 반드시 부모 노드를 하나 가진다.
트리의 아무 노드나 루트노드로 정해도 트리이다.
트리는 재귀적 구조를 가지고 있다. 트리는 서브트리를 포함하고, 서브트리 역시 트리이므로 서브트리를 포함한다.

트리 순회

전위 순회(preorder traversal) : 부모 방문 → 자식들 방문
후위 순회(postorder traversal) : 자식들 방문 → 부모 방문

이진트리

모든 노드에 대해 자식의 수가 최대 2인 트리
중위 순회(Inorder traversal)를 할 수 있다. 왼쪽 자식노드 방문 → 루트 노드 방문 → 오른쪽 자식 노드 방문

포화 이진트리

리프노드가 아닌 노드는 반드시 자식 노드를 둘 갖는다.
모든 리프 노드의 깊이가 같다.
높이가 h일때, 리프노드 : $2^h$개
노드 : $2^{h+1}-1$개
높이 : $O(log 노드수)$

트리의 재귀적 구조

재귀적인 그래프 탐색으로 구간 [L:R]의 구간합을 구할 수 있다. → DFS
높이가 $O(log N)$인 포화 이진 트리인 경우, O(log N)에 구간합을 구할 수 있다. 많아야 2*logN개의 노드 방문

트리에서의 다이나믹 프로그래밍

Tree DP
DP : 큰 문제를 부분 문제로 나누어 푸는 방법 전체 트리의 문제를 서브 트리의 해를 이용하여 풀 수 있다.
전위 순회와 후위 순회
DFS를 이용한 순회
부모와 자식 중 어느 쪽을 먼저 방문하는지 여부가 다르다.
전위 순회
부모 노드의 해를 결정하여 자식노드에게 전달

트리의 높이 구하기

  void dfs(int H) {
      ans = max(ans, H);
  		for (각 자식노드) {
  				dfs(H + 1)
  	}
  }

후위순회
서브 트리의 해를 이용해 전체 트리의 문제 해결
많은 트리 DP 문제에 해당

일반적인 구조

  func dfs(int v) {
  	for (sub_v : 자식노드들) {
  		dfs(sub_v)
  		dp[v] = dp[sub_v] 를 이용해 결정
  	}
  }

A - 트리의 부모 찾기

dfs로 탐색하여 1번 노드를 루트로 각 노드의 부모를 찾아주었다.

11725번 트리의 부모 찾기

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;
    priority_queue<pi,vector<pi>,greater<pi>> q;
    vector<vector<int>>v;
    int n;
    bool visit[100001];
    int parent[100001];
    void dfs(int x){
        if(visit[x])
            return;
        visit[x]=true;
        for(auto&i:v[x]){
            if(visit[i])continue;
            parent[i] = x;
            dfs(i);
        }
    }
    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        v.resize(n+1);
        for(int i=0,p1,p2;i<n-1;i++){
            cin>>p1>>p2;
            v[p1].push_back(p2);
            v[p2].push_back(p1);
        }
        dfs(1);
        for(int i=2;i<=n;i++){
            cout<<parent[i]<<endl;
        }
        return 0;
    }

B - 너구리 구구

dfs로 탐색하여 다음 코드로 문제를 풀었다. i.first = 자식 노드, i.second = 자식 노드까지의 cost

cost = max(cost,dfs(i.first)+i.second);

18126번 너구리 구구

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,ll> pi;

    priority_queue<pi,vector<pi>,greater<pi>> q;
    int n;
    vector<vector<pi>> v;
    bool visit[5001];
    ll dfs(int x){
        if(visit[x])
            return 0;
        visit[x] = true;
        ll cost =0;
        for(auto& i:v[x]){
            if(visit[i.first]) continue;
            cost = max(cost,dfs(i.first)+i.second);
        }
        return cost;
    }

    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        v.resize(n+1);
        for(int i=0,p1,p2;i<n-1;i++){
            ll c;
            cin>>p1>>p2>>c;
            v[p1].push_back({p2,c});
            v[p2].push_back({p1,c});
        }
        cout<<dfs(1);
    }

C - 인하니카 공화국

리프노드들의 cost합과 자신의 cost중 작은 것을 선택한다. 내가 구현한 코드에서 1번노드의 자식이 한개인 경우에 대해서 예외처리를 안해주어 계속 틀렸다. 다이나믹 프로그래밍이라 써있긴 하지만 dfs만 사용해도 풀렸다. dfs(v,i.first) → 리프노드들의 cost합, i.second = 자신의 cost를 의미한다.

cost += min(i.second,dfs(v,i.first));

12784번 인하니카 공화국

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    priority_queue<pi,vector<pi>,greater<pi>> q;
    int t,n,m;
    bool visit[1001];
    int dp[1001];
    int dfs(vector<vector<pi>>& v,int x){
        if(dp[x]!=-1)
            return dp[x];
        visit[x] = true;
        if(x!=1 && v[x].size()==1)
            return dp[x]=v[x].front().second;
        dp[x]=0;
        for(auto&i:v[x]){
            if(visit[i.first]) continue;
            dp[x] += min(i.second,dfs(v,i.first));
        }
        return dp[x];
    }

    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>t;
        while(t--){
            cin>>n>>m;
            vector<vector<pi>> v;
            v.resize(n+1);
            memset(visit,false,sizeof(visit));
            memset(dp,-1,sizeof(dp));
            for(int i=0,p1,p2,d;i<m;i++){
                cin>>p1>>p2>>d;
                v[p1].push_back({p2,d});
                v[p2].push_back({p1,d});
            }
            dfs(v,1);
            cout<<dp[1]<<'\n';
        }
        return 0;
    }

D - 트리 순회

전위,중위,후위 순회에 대한 문제였다.

1991번 트리순회

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    vector<vector<int>> v;
    priority_queue<pi,vector<pi>,greater<pi>> q;
    int n;
    void preorder(int x){
        char tmp = x+'A';
        cout<<tmp;
        for(auto& i:v[x]){
            if(i==('.'-'A'))continue;
            preorder(i);
        }
    }
    void postorder(int x){
        char tmp = x+'A';
        for(auto& i:v[x]){
            if(i==('.'-'A'))continue;
            postorder(i);
        }
        cout<<tmp;
    }
    void inorder(int x){
        char tmp = x+'A';
        char lc,rc;
        if(v[x][0]!=('.'-'A')) {
            inorder(v[x][0]);
        }
        cout<<tmp;
        if(v[x][1]!=('.'-'A')) {
            inorder(v[x][1]);
        }

    }
    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        v.resize(n+1);
        for(int i=0;i<n;i++){
            char p1,lc,rc;
            cin>>p1>>lc>>rc;
            v[p1-'A'].push_back(lc-'A');
            v[p1-'A'].push_back(rc-'A');
        }
        preorder(0);
        cout<<endl;
        inorder(0);
        cout<<endl;
        postorder(0);
    }

E - 단절점과 단절선

처음에 시간복잡도를 생각하지 않고 dfs 탐색했다가 시간초과가 났다. 이렇게 하면 O(10^10)인 것을 확인하고 다른 방법을 생각했다. 정점의 차수가 1인것을 제외한 모든 정점이 단절점이 된다. 모든 간선은 단절선이다.

14675번 단절점과 단절선

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    int n,q;
    bool visit[100001];
    int degree[100001];

    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        for(int i=1,p1,p2;i<n;i++){
            cin>>p1>>p2;
            degree[p1]+=1;
            degree[p2]+=1;
        }
        cin>>q;
        for(int i=0,t,k;i<q;i++){
            cin>>t>>k;
            if(t==1) {
                if (degree[k] == 1)
                    cout << "no" << endl;
                else
                a    cout << "yes" << endl;
            }
            else
                cout<<"yes"<<endl;
        }
        return 0;
    }

F - 전단지 돌리기

케니소프트 위치 S를 root로한 트리에서 각 노드의 높이를 DFS를 이용하여 구하면 된다. 다음은 각 노드의 높이를 구하는 코드이다. 문제에서 주어진 힘이 어떤걸 의미하는 지 몰라서 한참 헤맸다. 전단지 던지는 힘이었다. ㅋㅋ

for(auto&i:v[x]){
        if(visit[i])continue;
        h[x]= max(dfs(i)+1,h[x]);
    }

19542번 전단지 돌리기

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    vector<vector<int>> v;
    int n,s,d;
    bool visit[100001];
    int h[100001];

    int dfs(int x){
        visit[x]=true;
        h[x] =0;
        for(auto&i:v[x]){
            if(visit[i])continue;
            h[x]= max(dfs(i)+1,h[x]);
        }
        return h[x];
    }

    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n>>s>>d;
        v.resize(n+1);
        for(int i=0,p1,p2;i<n-1;i++){
            cin>>p1>>p2;
            v[p1].push_back(p2);
            v[p2].push_back(p1);
        }
        dfs(s);
        int dist=0;
        for(int i=1;i<=n;i++){
            if(i!=s && h[i]>d-1){
                dist+=1;
            }
        }
        cout<<dist*2<<endl;
    }

G - 회사 문화 1

한사람이 여러번 칭찬 받는 경우를 고려해야 한다. dfs를 이용하였고, 노드번호와 칭찬받는 정도를 함수 인자로 넘겨주었다.

14267번 회사문화1

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    vector<vector<int>> v;
    ll tk[100001];
    bool visit[100001];
    ll hm[100001];// how much

    void dfs(int x,ll k){
        visit[x]=true;
        hm[x]=k;
        for(auto&i:v[x]){
            if(visit[i])continue;
            dfs(i,k+tk[i]);
        }
    }
    int n,m;
    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n>>m;
        v.resize(n+1);
        for(int i=1,p1;i<=n;i++){
            cin>>p1;
            if(p1!=-1) {
                v[i].push_back(p1);
                v[p1].push_back(i);
            }
        }
        for(int i=0,p1,p2;i<m;i++){
            cin>>p1>>p2;
            tk[p1]+=p2;
        }
        dfs(1,tk[1]);
        for(int i=1;i<=n;i++){
            cout<<hm[i]<<' ';
        }
    }

H - 버스노선

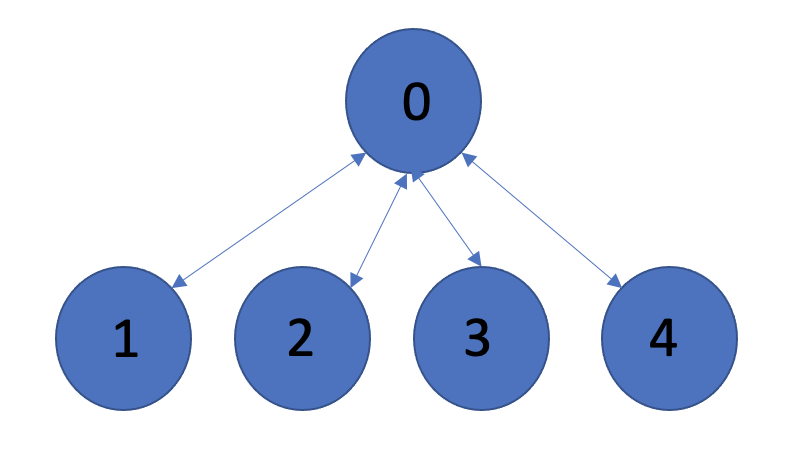
모든 도로에 적어도 하나 이상의 버스 노선이 지나가는 버스 노선의 최소 개수를 구하는 문제이다.

어떤 리프노드에서 다른 리프노드까지 도달하는 방법이라고 생각했다. 위와 같은 경우에 대해 1→0→2 /3/4으로 3가지가 나온다. 하지만 서로 다른 경로에서 출발점과 도착점이 아닌 경유 정류장은 겹칠 수 있으므로 1→0→2/3→0→4 : 2가지 이다.

dfs를 leaf 노드에서 시작하면 겹칠 수 있는 경우에 대해 고려할 수 없다. 그래서 dfs를 차수가 가장 높은 노드에서 시작하여 leaf 노드로 가는 경우의 수를 세준후, 2로 나누고 올림 하였다.

17842번 버스노선

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include  <cmath>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    vector<vector<int>> v;
    int n,root;
    bool visit[200001];

    int dfs(int x){
        visit[x] = true;
        int count = 0;
        if(v[x].size()==1 && x!=root)
            return 1;
        for(auto&i:v[x]){
            if(visit[i]) continue;
            count+=dfs(i);
        }
        return count;
    }
    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        v.resize(n);
        for(int i=0,p1,p2;i<n-1;i++){
            cin>>p1>>p2;
            v[p1].push_back(p2);
            v[p2].push_back(p1);
        }
        root = 0;
        for(int i=0;i<n;i++){
            if(v[i].size()>v[root].size()){
                root=i;
            }
        }

        int ans = dfs(root);
        if(ans%2==1)
            cout<<(ans+1)/2;
        else
            cout<<ans/2;
    }

I - 대기업 승범이네

못풀어서 해설을 참고했다. 홍익대 대회 자료 여기서 해설 읽고 구현하였다.

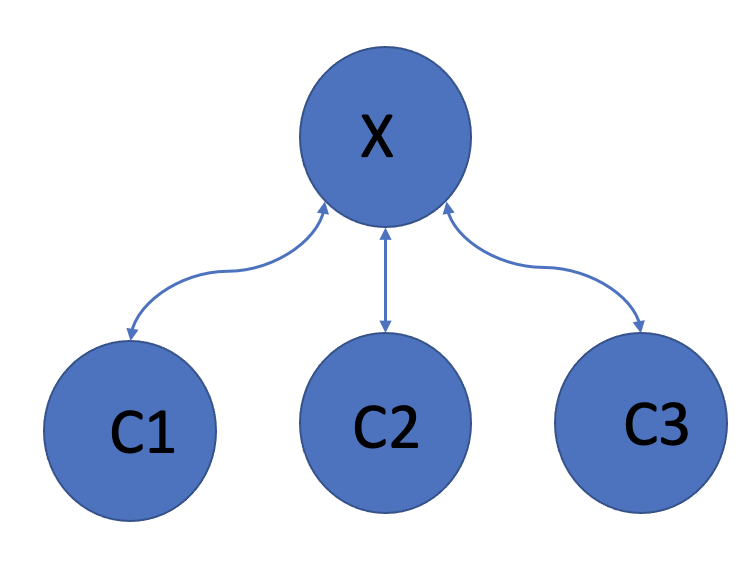
노드 x와 x의 서브트리가 있을때, 서브트리는 x가 멘토를 갖고있는 지만 관심이 있다. 즉, dp[x][hasMentor]를 사용하면 된다. (항상 dp 2차원배열이상으로 늘어나면 헤멘다..)

(1) dp[x][1] : x의 멘토가 있을 경우이다. 이때는 dp[x][1] = dp[c1][0]+dp[c2][0]+dp[c3][0]이 된다.

(2) dp[x][0] : x의 멘토가 없을 경우이다. 이때는 x-c1, x-c2, x-c3 가 사수-부수사인 경우를 (1)에 추가하여 고려해야 한다. dp[c1][0]~dp[c3][0]의 합을 미리 구해놓고 아래와 같이 구하면 된다. 미리 구한합에 dp[i][0]을 빼고, dp[i][1] + x능력 * i 능력 하면 된다.

(1) dp[x][1] = dp[x][1] = dp[c1][0]+dp[c2][0]+dp[c3][0];
(2) dp[x][0] = max(dp[x][0], no_mentor_su, - dp[i][0] +dp[i][1]+p[x]*p[i]);

17831번 대기업 승범이네

code

    #include <iostream>
    #include <cstring>
    #include <string>
    #include <algorithm>
    #include <vector>
    #include<queue>
    #define endl '\n'
    #define INF 1e9
    #define LINF 2e15

    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pi;

    vector<vector<int>> v;
    int n;
    ll p[200001];
    ll dp[200001][2];
    bool visit[200001];

    void dfs(int x){
        visit[x]=true;
        ll no_mentor=0;
        for(auto i:v[x]){
            if(visit[i])continue;
            dfs(i);
        }

        for(auto i:v[x])
            no_mentor+=dp[i][0];
        dp[x][1]=no_mentor;
        dp[x][0]=no_mentor;
        for(auto i:v[x]) {
            dp[x][0] = max(dp[x][0], no_mentor - dp[i][0] +dp[i][1]+p[x]*p[i]);
        }
    }
    int main(){
        ios::sync_with_stdio(false);
        cin.tie(NULL);
        cin>>n;
        v.resize(n+1);
        for(int i=2,p1;i<=n;i++){
            cin>>p1;
            v[p1].push_back(i);
        }
        for(int i=1;i<=n;i++){
            cin>>p[i];
        }

        ll ans =0;
        dfs(1);
        cout<<max(dp[1][0],dp[1][1]);

    }

ChangHyeon Nam's Blog notes and thoughts

트리(Tree)

트리의 조건

용어

트리의 성질

트리 순회

이진트리

포화 이진트리

트리의 재귀적 구조

트리에서의 다이나믹 프로그래밍

A - 트리의 부모 찾기

B - 너구리 구구

C - 인하니카 공화국

D - 트리 순회

E - 단절점과 단절선

F - 전단지 돌리기

G - 회사 문화 1

H - 버스노선

I - 대기업 승범이네