그래프(Grpah) 와 관련된 이론
28 Jul 2021
CTP 알고리즘 동아리에서 여름방학 코딩테스트반에 참여하여 공부한 내용입니다.
A - 섬의 개수
DFS로 싸이클에 속한 정점을 찾을 수 있습니다. 정점 방문을 시작했는지에 대한 visited 배열 말고, 그 정점의 방문 함수가 완전히 끝났는지를 나타내는 finished 배열이 하나 더 필요합니다. DFS를 하다가 visited[k] = true, finished[k]=false인 경우, 사이클이 발생합니다.
A번 문제는 연결 그래프의 개수 (컴포넌트의 개수)를 세는 문제였습니다. 이차원 배열에 대해 8방향으로 이동할 수 있었습니다. dfs를 이용하여, 한번 탐색할때, 1로 연결된 육지를 모두 방문해주었습니다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
int dy[]={1,-1,0,0,1,-1,1,-1};
int dx[]={0,0,-1,1,1,-1,-1,1};
priority_queue<pi,vector<pi>,greater<pi>> q;
int w,h;
int arr[50][50];
bool visited[50][50];
int dfs(int y,int x){
if(visited[y][x] || arr[y][x]==0)
return 0;
visited[y][x] = true;
for(int i=0;i<8;i++){
int ny = y+dy[i];
int nx = x+dx[i];
if(ny<0 || ny>=h || nx<0 || nx>=w || arr[ny][nx]==0 || visited[ny][nx])
continue;
dfs(ny,nx);
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
while(1) {
cin >> w >> h;
int count = 0;
if(w==0 && h==0)
break;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
visited[i][j]= false;
cin >> arr[i][j];
}
}
for(int i=0;i<h;i++){
for(int j=0;j<w;j++){
if(!visited[i][j] && arr[i][j]==1)
count+=dfs(i,j);
}
}
cout<<count<<'\n';
}
}
B -타임머신
이 문제는 벨만-포드 알고리즘을 사용하는 문제이다. 저번주에 공부한 다익스트라에서 가중치(cost)가 음수인 경우를 다루는 알고리즘이 벨만-포드 알고리즘이라고 했다.
벨만-포드 알고리즘(Bellman-Ford algorithm)은 다익스트라 알고리즘과 마찬가지로 시작점을 정해주면, 다른 모든 정점으로의 최단 경로를 구한다. 다익스트라가 O(ElogV)가 걸린데 비해, 벨만-포드를 모든 정점에 대해 돌리면 O(VE)로 시간이 더 걸린다.
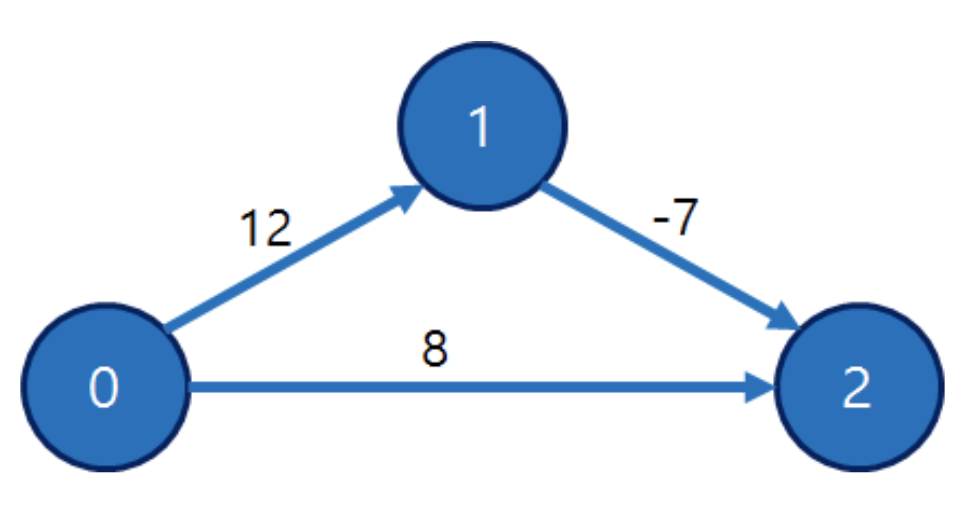
위 그래프에 대해 2번 정점까지 도달하는 최단거리를 구한다고 하자. 다익스트라 알고리즘을 이용하면, 0번에서 시작했을때, 0→1→2가 아닌 0→2로 이동할 것이다. (12>8) 이므로. 즉, 음의 간선이 있을 경우 최단 경로를 제대로 못 구할 수 있다.
따라서 벨만 포드 알고리즘은 2중 for문을 통해 철저하게 가능한 모든 경우를 다 체크한다. 최단 경로의 간선의 최대 개수는 V-1개 이므로, 루프를 V-1번 돈다. 따라서 루프를 V-1번 돌리는데, k번째 루프에서는 시작점으로부터 각 정점으로 k개의 간선을 거쳐서 도달할 수 있는 최단경로를 다 갱신해주자는 것이 기본 아이디어 이다. k-1번째 루프까지 최대 k-1개의 간선을 거치는 최단경로를 구해놓고, k번째 루프에서는 그 정보들을 사용해 또 다른 최단 경로를 구해보는 것이다.
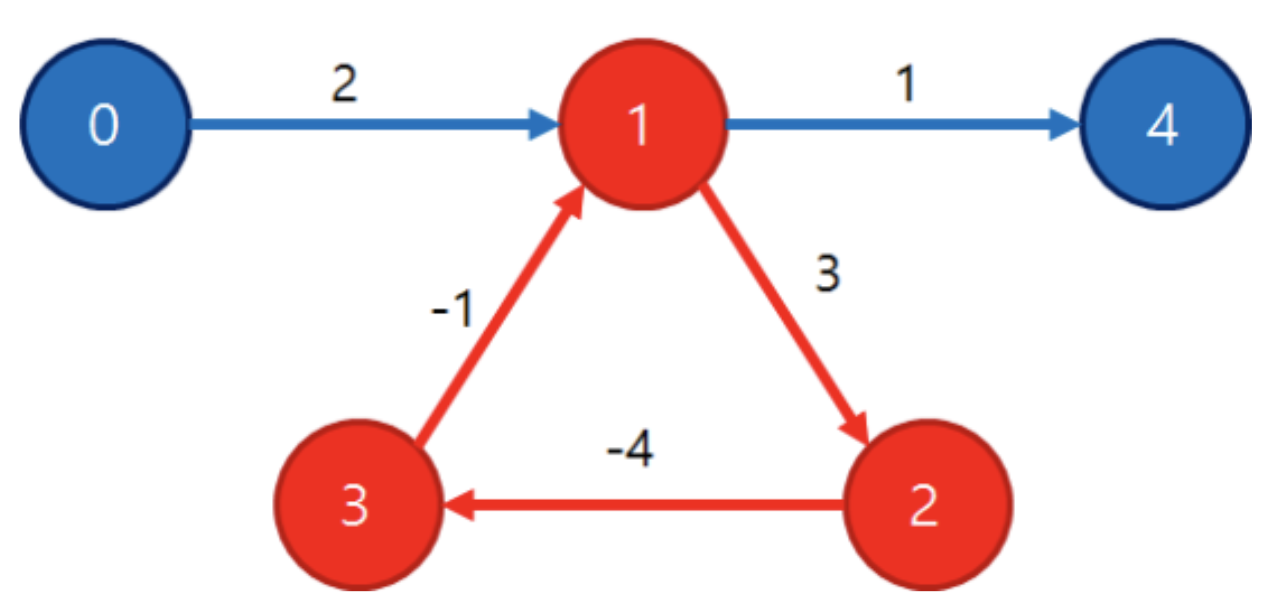
여러가지 경우에 대해 고려해야 하지만, 위의 경우가 신기하여 정리 해보겠습니다. 0번에서 4번까지 가는 최단거리가 0→1→4가 아닌 0→1→2→3→4 입니다. 지금까지의 최단거리는 같은 정점을 두번 이상 지나지 않는다고 믿었지만, 위의 경우는 다릅니다. 위의 경우 무한 음의 사이클을 돌면 dist[4] = -INF가 됩니다.
이렇게 가중치 합이 0보다 작은 싸이클은 음수 싸이클 혹은 음의 사이클 (negative cycle)이라 하며 벨만-포드 관련 문제에서 반드시 등장하는 요소입니다. B번 문제에서는 음의 사이클이 하나라도 존재하면 ‘-1’을 출력하라고 했다.
만약 음의 사이클이 존재한다면, 그 이후에 루프를 돌면 최단거리가 갱신되지 않는 일이 발생합니다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
//vector<vector<pi>> v;
//priority_queue<pi,vector<pi>,greater<pi>> q;
ll dist[500];
int n,m;
vector<vector<pi>> v;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m;
v.resize(n+1);
for(int i=0,p1,p2,p3;i<m;i++){
cin>>p1>>p2>>p3;
v[p1].push_back({p2,p3});
}
bool minusCycle = false;
fill(dist+1,dist+1+n,LINF);
dist[1]=0;
for(int i=0;i<n;i++){ // n-1번의 루프
for(int j=1; j<=n;j++){
// n-1번의 루프에 걸쳐 각 정점이 i+1개 정점을 가져오는 최단경로 갱신
for(auto& k:v[j]){
int next = k.first, d = k.second;
if(dist[j] !=LINF && dist[next]>dist[j]+d){
dist[next] = dist[j] + d;
// n번째 루프에 값이 갱신 되면
if(i==n-1) minusCycle =true;
}
}
}
}
if(minusCycle){
cout<<-1<<endl;
return 0;
}
for(int i=2;i<=n;i++)
cout<<(dist[i]!=LINF ? dist[i]:-1)<<endl;
return 0;
}
C - 플로이드
플로이드 와샬 알고리즘 (Floyd-Warshall algorithm), 줄여서 플로이드라고 한다. 다익스트라와 벨만-포드와 다르게 정점 V개가 있고 거리가 다 주어져 있을때 한번 시행으로 모든 정점 쌍 사이의 거리를 다 구해 냅니다. 3중 for문으로 O(V^3)이 걸린다. 음의 가중치가 있는 간선 그래프에서도 제대로 동작합니다.
플로이드는 최단경로를 dp형태의 문제로 정의하고 풀어냅니다. shortestPath(i,j,k) : i번 정점에서 j번 점점까지 1~k번 정점만 사용할 때의 최단거리를 의미한다. k단계 문제를 풀려면 k-1 단계의 정보가 필요한데, k= 1~N까지 시도하며 정보를 계속해서 갱신하게 된다.
k-1단계 이전의 정보는 더이상 필요하지 않아 3차원 배열을 쓰지 않고 슬라이딩 윈도우 기법을 이용하여 덮어써서 2차원 배열 dist만 가지고도 해결이 돕니다. 벨만-포드 알고리즘과 비슷하게 k번의 루프를 돌려보면 마지막엔 더 이상 갱신되지 않는 최단 경로 배열 dist가 완성됩니다.
k단계, 1~k번 정점을 사용하여 도달 가능한 최단거리를 구해야하는 단계라고 하자. dist 배열에는 1~k-1 번 정점만 사용해서 나올 수 있는 최단거리가 있다. 이것을 사용해서 갱신한다.
어떤 두 정점 i,j에 대해 k번 정점을 사용해 우회하면 지금까지보다 최단거리가 짧아지는가? 이 질문에 모든 i,j 쌍에 대해 던져보고 그렇다면 갱신한다. query는 다음과 같다.
if(dist[i][j] > dist[i][k] + dist[k][j])
dist[i][j]는 지금까지 찾은 최단거리를 담고있고, k번 정점을 새로 우회하여 가는 경로가 더 빠를 수도 있는데 그것을 묻고 있는 것이다.
정점 V개에 대한 모든 정점에서 다익스트라 알고리즘을 돌리면 O(V(E+VlogV))이고, 만약 간선개수가 V^2보다 많아진다면 다익스트라가 더 좋지만 음의 가중치에서는 사용하지 못한다. 벨만 포드 알고리즘을 모든 정점에 대해 돌리면 O(V^2*E)이므로 플로이드가 무조건 우위입니다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
int n,m;
int dist[100][100];
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
dist[i][j] = i==j ? 0: INF;
}
}
for(int i=0,p1,p2,p3;i<m;i++){
cin>>p1>>p2>>p3;
dist[p1-1][p2-1] = min(dist[p1-1][p2-1],p3);
}
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
dist[i][j] = min(dist[i][j],dist[i][k]+dist[k][j]);
for(int i=0;i<n;i++) {
for (int j = 0; j < n; j++) {
if (dist[i][j]==INF)
cout<<0<<" ";
else
cout << dist[i][j] << " ";
}
cout<<endl;
}
return 0;
}
D - 적록색약
dfs로 적록색약일 경우와 아닐 경우에 대해 고려하여 풀면 되는 문제였다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
vector<vector<pi>> v;
priority_queue<pi,vector<pi>,greater<pi>> q;
int n;
int arr[100][100];
int dy[]={1,-1,0,0};
int dx[]={0,0,1,-1};
bool visit[100][100];
int dfs_normal(int y,int x){
if(visit[y][x])
return 0;
visit[y][x]=true;
char color = arr[y][x];
for(int i=0;i<4;i++){
int ny,nx;
ny = y+dy[i];
nx = x+dx[i];
if(ny<0 || ny>=n || nx<0 || nx>=n || color!=arr[ny][nx])
continue;
dfs_normal(ny,nx);
}
return 1;
}
int dfs_abnor(int y,int x){
if(visit[y][x])
return 0;
visit[y][x]=true;
char color = arr[y][x];
for(int i=0;i<4;i++){
int ny,nx;
ny = y+dy[i];
nx = x+dx[i];
if(ny<0 || ny>=n || nx<0 || nx>=n )
continue;
if((color=='R'||color=='G')&&(arr[ny][nx]=='R'||arr[ny][nx]=='G'))
dfs_abnor(ny,nx);
else if(color=='B'&&arr[ny][nx]=='B')
dfs_abnor(ny,nx);
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >>n;
for(int i=0;i<n;i++){
string str;
cin>>str;
for(int j=0;j<n;j++){
arr[i][j]=str[j];
}
}
int count_normal =0;
int count_abnormal = 0;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(!visit[i][j])
count_normal+=dfs_normal(i,j);
}
}
memset(visit,false,sizeof(visit));
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
if(!visit[i][j])
count_abnormal+=dfs_abnor(i,j);
}
} cout<<count_normal<<' '<<count_abnormal;
return 0;
}
E - 욕심쟁이 판다
dp + dfs 문제였다. 아래와 같은 쿼리로 풀 수 있었다.
if(arr[y][x]<arr[ny][nx]) {
ret = max(dfs(ny, nx) + 1, dp[ny][nx]);
}
시간 복잡도는 $O(N^2 + 4*N^2) = O(5N^2)$ 이다. 1937번 욕심쟁이 판다
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
vector<vector<pi>> v;
priority_queue<pi,vector<pi>,greater<pi>> q;
int dy[]={1,-1,0,0};
int dx[]={0,0,1,-1};
bool visit[500][500];
int dp[500][500];
int arr[500][500];
int n;
int dfs(int y,int x){
int&ret =dp[y][x];
if(ret!=0)
return ret;
ret = 1;
visit[y][x]=true;
for(int i=0;i<4;i++){
int ny,nx;
ny = y+dy[i];
nx = x+dx[i];
if(ny<0||ny>=n||nx<0||nx>=n||arr[y][x]>=arr[ny][nx])
continue;
if(arr[y][x]<arr[ny][nx]) {
ret = max(dfs(ny, nx) + 1, ret);
}
}
return ret;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
cin>>arr[i][j];
}
int ans = -1;
memset(dp,0,sizeof(dp));
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
if(!visit[i][j])
ans=max(dfs(i,j),ans);
}
cout<<ans<<'\n';
return 0;
}
F - 양 구출 작전
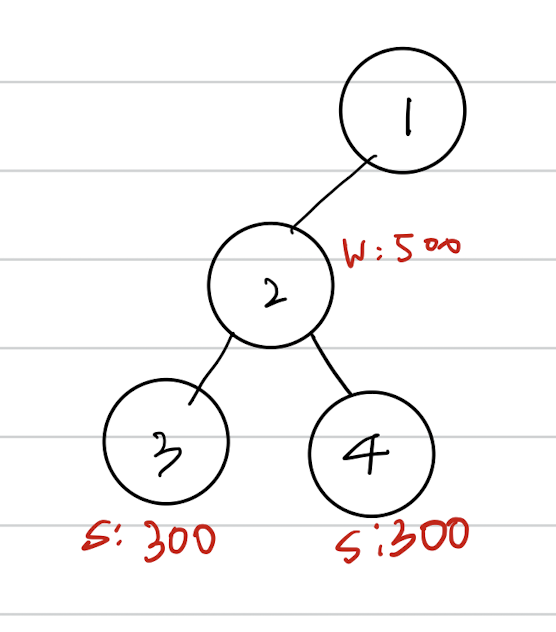
3번과 4번 섬의 양의 수의 합이 2번 섬의 늑대의 수보다 클 경우 100마리가 살아남는다. ← 처음에 각 섬을 독립적으로 생각해서 2번 섬까지 살아 남는 양이 없다고 생각했다. 이 경우를 제외하곤 평범한 dfs문제였다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,ll> pl;
vector<vector<int>> v;
vector<pl> w;
int n;
ll dfs(int x){
int animal;
if(v[x].empty()) {
if (w[x].first == 1)
return w[x].second;
else
return 0;
}
animal = w[x].first;
ll count = 0;
for(auto& i : v[x]){
count += dfs(i);
}
if(animal==1)
count+=w[x].second;
if(animal==0)
{
if(count>w[x].second)
count -=w[x].second;
else
count =0;
}
return count;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
v.resize(n+1);
w.resize(n+1);
w[1]={1,0};
for(int i=2,p1;i<=n;i++){
ll num;
char sw; // sheep or wolf
cin>>sw>>num>>p1;
if(sw=='S') {
v[p1].push_back(i);
w[i]={1,num};
}
if(sw=='W') {
v[p1].push_back(i);
w[i]={0,num};
}
}
cout<<dfs(1);
}
G - Two Dots
dfs를 그냥 쓰면 이미 방문한 노드에서 시작해서 cycle이 발생하는 경우를 고려해야 한다. n≤50,m≤50 이었기 때문에 4중 for문을 써도 1초 안이다. 그래서 모든 좌표에 대해 dfs를 돌려주되, 해당 dfs를 통해 visit한 좌표는 false여야 했다.
이 문제를 틀린 가장 큰 이유는 Yes → YES, No → NO 로 써서 틀렸다. (ㅋㅋ…)
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
vector<vector<pi>> v;
priority_queue<pi,vector<pi>,greater<pi>> q;
int n,m;
char arr[50][50];
int dy[]={1,-1,0,0};
int dx[]={0,0,1,-1};
bool visit[50][50];
bool dfs(int y, int x,int begin_y,int begin_x,int count){
if(visit[y][x]&&y==begin_y && x==begin_x &&count>=4) {
return true;
}
if(visit[y][x])
return false;
visit[y][x]=true;
bool ans = false;
char tmp = arr[y][x];
for(int i=0;i<4;i++){
int ny = y+dy[i];
int nx = x+dx[i];
if(y<0||y>=n||x<0||x>=m||arr[ny][nx]!=tmp)
continue;
ans = dfs(ny,nx,begin_y,begin_x,count+1);
if(ans)
return ans;
}
return ans;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
bool ans = false;
cin>>n>>m;
for(int i=0;i<n;i++){
string str;
cin>>str;
for(int j=0;j<m;j++)
{
arr[i][j]=str[j];
}
}
memset(visit,false,sizeof(visit));
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(!visit[i][j])
ans = dfs(i,j,i,j,1);
if(ans)
{
cout<<"Yes"<<endl;
return 0;
}
memset(visit,false,sizeof(visit));
for(int l=0;l<=i;l++){
for(int k=0;k<=j;k++)
visit[l][k]=true;
}
}
}
cout<<"No"<<endl;
return 0;
}
H - 상남자
처음 플레티넘문제를 풀어봤다. 플레티넘V는 넘사벽이라 할만큼 어렵지는 않은것 같다. BFS 문제였는데, 처음에는 위아래좌우 한칸씩 방문했더니 틀렸다. 문제에서 위아래로 1이아닌 곳까지 무한으로 이동할수 있기때문에, 위아래에 대해 최대한 방문해줘야 한다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include<queue>
#define endl '\n'
#define INF 1e9
#define LINF 2e15
using namespace std;
typedef long long ll;
typedef pair<int,int> pi;
typedef pair<pi,pi> piii;
queue<piii>q;
int n,m;
int arr[1000][1000];
bool visit[1000][1000];
int dy[]={1,-1};
int lx[]={-1};
int rx[]={1};
int L,R;
int bfs(int y,int x, int count_l, int count_r){
int count = 0;
q.push({ {y,x},{count_l,count_r}});
while(!q.empty()){
int by,bx,cl,cr;
by = q.front().first.first;
bx = q.front().first.second;
cl = q.front().second.first;
cr = q.front().second.second;
if(visit[by][bx]) // 다시 방문했다면, 위아래로 쭉 또 이동할 필요가 없다.
{
q.pop();
continue;
}
if(!visit[by][bx])
count+=1;
visit[by][bx]=true;
q.pop();
for(int i=0;i<2;i++){
int ny,nx;
ny = by;
nx = bx;
int addy = dy[i];
for(int j=0;j<n;j++){
ny+=addy;
if(ny<0||ny>=n||nx<0||nx>=m||visit[ny][nx])
continue;
if(arr[ny][nx]==1) // 위아래로 쭉 움직이다가 벽이 있으면 break
break;
q.push({{ny,nx},{cl,cr}});
}
}
int lnx,rnx;
lnx = bx + lx[0];
rnx = bx + rx[0];
if(lnx>=0 && lnx<m && !visit[by][lnx] && arr[by][lnx]!=1 && cl<L) {
q.push({{by, lnx},{cl+1,cr}});
}
if(rnx>=0 && rnx<m && !visit[by][rnx] && arr[by][rnx]!=1 && cr<R){
q.push({{by,rnx},{cl,cr+1}});
}
}
return count;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m>>L>>R;
int pos_y,pos_x;
for(int i=0;i<n;i++){
string str;
cin>>str;
for(int j=0;j<m;j++){
arr[i][j]=str[j]-'0';
if(arr[i][j]==2) {
pos_y=i;
pos_x=j;
}
}
}
cout<<bfs(pos_y,pos_x,0,0);
return 0;
}
reference
(1)플로이드 와샬 알고리즘