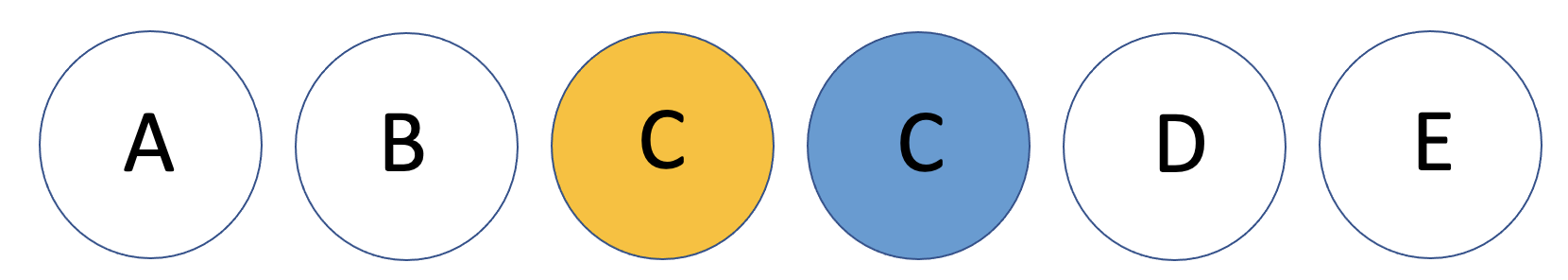이진 탐색(Binary Search)
21 Jul 2021
CTP 알고리즘 동아리에서 여름방학 코딩테스트반에 참여하여 공부한 내용입니다.
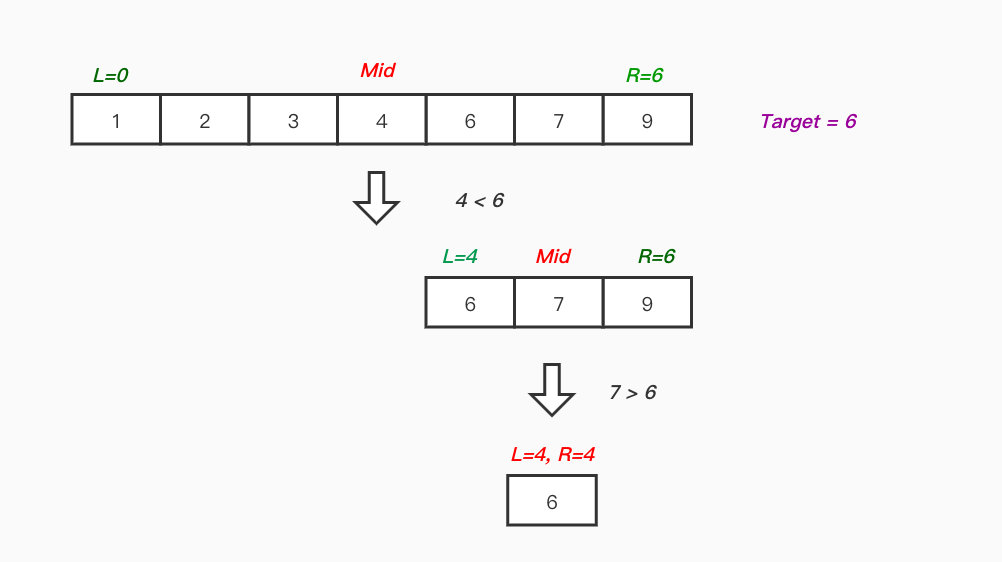
이진 탐색은 탐색 알고리즘 중 하나이다. 오름차순으로 정렬된 리스트의 중간 값을 임의의 값으로 선택하여 찾고하자 하는 key 값과 비교하는 방식으로 돌아가는 알고리즘이다. 정렬된 리스트에서만 사용가능하고, O(logN)이 걸린다.
위 그림에서 6을 찾으려 할때, 탐색 index를 start =0, end = 6, mid= 3으로 시작하여 1/2씩 탐색 범위를 줄여가며 찾는 방법이다. 가장 기본적인 예시가 A - 수찾기이다.
A - 수 찾기
N개의 정수 A[1], A[2], …, A[N] 가 주어지고, M개의 수들이 주어지는데, 이 수들이 배열 A안에 존재하는지 알아내면 된다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int n,m;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
vector<int>v(n);
for(auto&i :v)
cin>>i;
cin>>m;
sort(v.begin(),v.end()); // 이진 탐색을 위해 vector를 sort 시킴.
for(int i=0;i<m;i++){
int input;
cin>> input;
bool found = false;
int st = 0, en = n-1; // start =0, end = n-1.
while(st<=en){
int mid = (st+en)/2; // 중간값.
int cur = v[mid];
if(cur==input) { // 찾으려는 값이 현재 범위의 중간값일 경우.
found = true;
break;
}
if(cur<input) // 찾으려는 값이 현재 범위의 중간값보다 클 경우 start=mid+1.
st = mid+1;
if(cur>input) // 찾으려는 값이 현재 범위의 중간값보다 작을 경우 end=mid-1.
en = mid-1;
}
if(found)
cout<<1<<'\n';
else
cout<<0<<'\n';
}
return 0;
}
B번 문제는 Parametric Search(파라메트릭 서치)에 관한 문제이다. 파라메트릭 서치는 이진탐색과 다르게 주어진 일련의 값들이 아니라 주어진 범위 내에서 원하는 값 또는 원하는 조건에 가장 일치하는 값을 찾아내는 알고리즘이다. 그래서 파라메트릭 서치를 사용하면 최적화 문제를 결정 문제로 바꾸어 풀 수 있게된다. 예를 들어, 최솟값, 최댓값을 구하는 문제를 특정값이 어떠한 조건이 만족하는지만 확인하면 문제로 바뀐다는 뜻이다.
종만북 [12단원 최적화 문제 결정 문제로 바꾸어 풀기] 을 보면 구체적인 설명이 나와 있다. 최적화 문제를 결정문제 바꾸는 예시를 TSP 문제로 설명한다.
- optimize(G) = 그래프 G의 모든 정점을 한 번씩 방문하고 시작점으로 돌아오는 최단 경로의 길이를 반환한다. ( 최적화 문제)
- decision(G,x) = 그래프 G의 모든 정점을 한번씩 방문하고 시작점으로 돌아오면서 길이가 x이하인 경로의 존재 여부를 반환한다. (결정 문제)
optimize()는 가장 짧은 경로의 길이를 반환하지만, decision()은 최단 경로건 아니건 간에 x보다 짧은 경로가 있는지만 확인하면 된다. 종만북에 나와있는 최적화 문제 모두 이분탐색으로 풀 수 있다.
B - 나무 자르기
적어도 M미터의 나무를 집에 가져가기 위해서 설정할 수 있는 높이의 최댓값을 출력한다. → 최적화 문제인데, M미터 이상의 나무를 집에 가져가기 위한 높이라고 하면 결정 문제가 된다.
주어진 범위에서 mid = (start+end)/2이고, 자른 나무 길이의 합을 cur이라고 하자. cur≥m일때, mid의 최대값을 구하는 문제이다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
ll n,m;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m;
vector<int>v(n);
for(auto&i:v)
cin>>i;
sort(v.begin(),v.end());
ll st =0,en=1000000000;
ll ans = 0;
while(st<=en){
ll mid = (st+en)/2; // mid 값, 결정하려는 값.
ll cur = 0; // 현재 자른 나무의 합
for(auto&i : v){
ll tmp = i-mid;
if(tmp>=0)
cur+=tmp;
}
if(cur>=m) {
ans = max(mid,ans);
st = mid + 1;
}
if(cur<m)
en = mid-1;
}
cout<<ans<<'\n';
}
C번 문제는 C++의 binary_search, lower_bound를 활용하면 쉽게 풀 수 있다. 이진 탐색은 앞서 말했다 시피, container가 오름차순으로 sort되어야 한다.
-
binary_search(start_ptr, end_ptr, num): 이 함수는 element가 container에 존재할때 boolean true값을 반환하고, 그 외로는 false를 반환한다. lower_bound(start_ptr, end_ptr, num)반환하는 경우가 세가지가 있다.- container에 num에 해당하는 값이 하나 있을 경우, num의 위치를 가르키는 포인터를 반환한다.
- container에 num에 해당하는 값이 여러개 있을 경우, 첫번째 num에 해당하는 위치를 가리키는 포인터를 반환한다.
- num에 해당하는 값이 없을 경우 num 다음으로 큰 값의 위치를 가리키는 포인터를 반환한다.lower_bound의 반환값에서 첫번째 인자의 위치를 실제 index값을 구할 수 있다.
upper_bound(start_ptr, end_ptr, num): 반환하는 경우가 세가지가 있다.- container에 num에 해당하는 값이 하나 있을 경우, num 다음으로 큰 숫자의 위치를 가르키는 포인터를 반환한다.
- container에 num에 해당하는 값이 여러개 있을 경우, num 다음 으로 큰 첫번째 숫자에 해당하는 위치를 가리키는 포인터를 반환한다.
- num에 해당하는 값이 없을 경우 num 다음으로 큰 값의 위치를 가리키는 포인터를 반환한다. upper_bound의 반환값에서 첫번째 인자의 위치를 실제 index값을 구할 수 있다.
binary_search()는 return type이 boolean이기 때문에 해당 원소가 있는지 없는지 확인하는 용도로 사용한다.
오름차순으로 정렬된 리스트에서 특정 범위에 속하는 숫자들이 몇개 있는지 탐색하거나, 특정한 숫자가 몇번 나오는지 탐색하고자 할때 lower_bound(), upper_bound()를 사용하면 O(logN)시간에 탐색 가능합니다.
effective STL 책에서는 lower_bound, upper_bound()는 컨테이너의 정렬 상태를 깨지 않고 원소를 삽입할 수 있는 위치를 찾아주는 함수라고 설명한다. equal_range()는 lower_bound(), upper_bound() 결과를 쌍으로 던져 준다. 추가로 빠른 검색을 위해서라면 O(log N)을 보장하는 balancing binary search tree인 map을 사용하거나 hash table을 사용하되, 삽입 삭제가 빈번하지 않다면 vector를 이용하여, binary_search 사용을 고려해볼만 하다.
C - Sort 마스터 배지훈의 후계자
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
ll n,m;
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m;
vector<ll>v(n);
for(auto& i : v)
cin>>i;
sort(v.begin(),v.end());
for(int i=0;i<m;i++){
ll input;
cin>>input;
if(!binary_search(v.begin(),v.end(),input))
{
cout<<-1<<'\n';
continue;
}
else{
cout<<lower_bound(v.begin(),v.end(),input)-v.begin()<<'\n';
}
}
return 0;
}
D - 수열과 헌팅
n개의 원소중 i번째 원소를 x라고 하자. x의 하한은 n개의 원소들의 상한에서의 lowe bound이고, x의 상한은 n개의 원소들의 하한에서 upper bound - 1이다. index가 1부터 시작하므로 1씩 더해준다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
int n;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
vector<int>a;
vector<int>a1;
vector<int>b;
vector<int>b1;
for(int i=0;i<n;i++){
int v,w;
cin>>v>>w;
a.push_back(v-w);
b.push_back(v+w);
}
a1=a;
b1=b;
sort(a.begin(),a.end());
sort(b.begin(),b.end());
for(int i=0;i<n;i++){
int st=0,en=0;
st = lower_bound(b.begin(),b.end(),a1[i])-b.begin();
en = upper_bound(a.begin(),a.end(),b1[i])-a.begin()-1;
cout<<st+1<<' '<<en+1<<'\n';
}
}
E IF문 좀 대신 써줘
비내림차순으로 입력이 주어지기 때문에 따로 sort할 필요는 없다. 처음에 vector<pair<int,string»으로 접근했으나, pair<int,string>인 경우 비교자를 따로 선언하여도 lower_bound가 작동을 안했다. 그래서 그냥 map<int,string>으로 바꾸어 풀었다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
typedef long long ll;
int n,m;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n>>m;
map<int,string>v;
vector<int>w(m);
for(int i=0;i<n;i++){
string str;
int tmp;
cin>>str>>tmp;
v.insert({tmp,str});
}
for(auto& i : w)
cin>>i;
map<int,string>::iterator iter;
for(int i=0;i<m;i++){
iter = v.lower_bound(w[i]);
cout<<iter->second<<'\n';
}
}
F - Square, Not Rectangle
1≤ $H_{i}$≤ $10^9$ 에 대해 이진탐색을 하면 된다.
20033번 : Square, Not Rectangle
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
typedef long long ll;
int n;
int ans =0;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
vector<int>v(n);
for(auto& i : v) cin>>i;
int st =1, en = 1e9;
while(st<=en){
int mid = (st+en)/2;
int t = 0;
bool check = false;
for(int i=0;i<n;i++){
if(v[i]>=mid) t++;
else t = 0;
if(t>=mid) {
check = true;
break;
}
}
if(check) {
ans = mid;
st = mid + 1;
}
else
en = mid-1;
}
cout<<ans<<'\n';
}
G - 챔피언 (Easy)
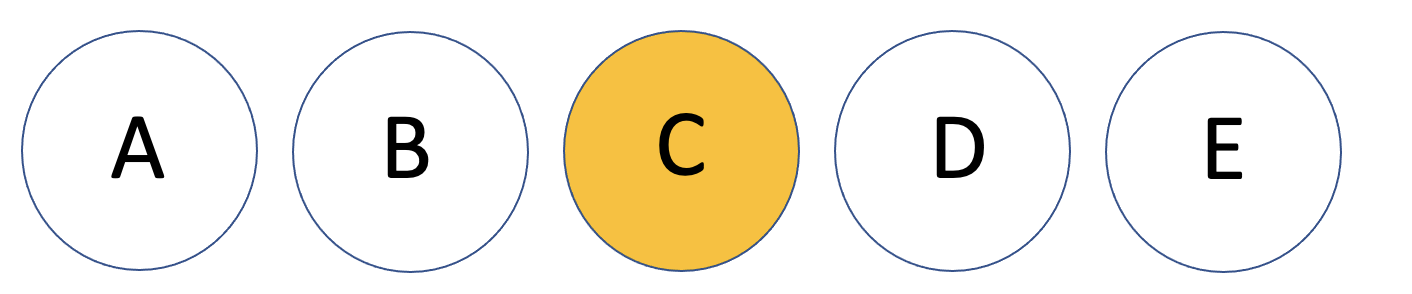
5명의 선수가 있다고 했을때, 챔피언이 되는 가장 작은 전투력의 선수를 찾으면 된다. C가 챔피언이 되는 가장 작은 전투력의 선수라면, A와B는 챔피언이 될수 없고, D,E는 챔피언이 될 수 있다. C,D,E가 챔피언이 되는 경우는 단조성이 유지되는 경우에만 해당한다.
하지만 위와 같이 같은 숫자의 선수가 있다면 단조성이 깨진다. 그래서 같은 전투력의 선수들을 고려하여 가장 왼쪽 선수들만 취해야 한다. 단조 증가하지 않는 경우에 대해서 이분 탐색시 en = mid-1(탐색의 끝지점)로 만들어서, 더 왼쪽 만을 취했다.
code
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
int n;
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
cin>>n;
vector<int>v;
for(int i=0;i<n;i++){
int tmp;
cin>>tmp;
v.push_back(tmp);
}
int ans = -1;
int st=0,en=v.size()-1;
while(st<=en){
int mid = st+en>>1;
int tmp = v[mid];
bool check = true; // mid 인덱스의 챔피언 가능 여부
for(int i=0;i<mid;i++){
if(v[i]<tmp){
tmp+=1;
}
else {
check = false;
break;
}
}
for(int i=mid+1;i<v.size();i++){
if(tmp>v[i]){
tmp+=1;
}
else{
check = false;
break;
}
}
if(check){
ans = mid;
en = mid-1;
}
else{
st = mid+1;
}
}
if(ans==-1)
cout<<-1<<'\n';
else{
cout<<ans+1<<' ';
for(int i=ans+1;i<v.size();i++)
{
if(v[i]!=v[i-1])
cout<<i+1<<' ';
}
cout<<'\n';
}
return 0;
}